基于抽象素养发展的数学教学研究

［摘  要］ 近年来，核心素养的培养成为学科教学的主要目标. 抽象素养作为数学学科核心素养的重要组成部分，受到广大教育工作者的重视. 准确划分抽象素养的水平层次，对课堂教学具有指导意义，可从情境创设、变式训练与实际应用等方面培养抽象素养.

［关键词］ 抽象素养；情境；变式；应用

随着新课改的推进，我国的数学教育教学已经成功从“知识立意”转变到“能力立意”，将学生“四基”“四能”“三会”等的发展放在教学首位，以学生数学学科核心素养的培养作为教学目标. 抽象素养作为核心素养的六大要素之一，对促进学生的发展具有重要意义.

■ 抽象素养的水平界定

数学抽象从数量关系和空间形式上揭示客观对象的本质和规律，培养数学抽象素养是促进学生数学理性思维形成的基本措施. 新课标提出：高中数学教学需注重对学生数学抽象素养的培养，这是促进学生全面发展的基础. 数学抽象素养的水平界定和评价如下：

水平一，学生能通过对实际情境的观察、分析与思考，自主抽象出相应的命题、概念、数学思想方法等，能借助原有数学方法与经验解决实际问题. 从知识与技能目标的角度来看，能透过问题情境发现知识本质，学会用数学思维来分析与思考现实生活问题，用数学语言来表达相应的知识. 在交流与反思层面，学生能自主解释数学概念、命题与法则等.

水平二，学生能在有关联的情境中抽象概念或命题，学会知识正迁移的方法，会推广相关命题. 知识与技能上能借助例举法来解释、构建概念等. 在思维与表达层面，要求学生具有自我总结与解决问题的能力，并将所学知识灵活地应用在实际问题中.

水平三，学生能从简单的情境中抽象问题并重新建构命题，用数学方法来解决相关问题等. 知识与技能方面要求学生掌握数学特征，感悟与体验知识本质，并能用精准的语言进行表达. 该水平阶段要求学生在交流与反思时，会用数学原理与概念来解释相关的社会与自然现象.

通过对高中生数学抽象素养的调查与分析，发现大部分学生处于水平一的状态，而水平二、水平三的得分相对较低. 由此可见，想要发展学生的数学抽象素养，还需要教师从深层次的教学出发，通过各种教学手段不断强化学生的抽象能力，发展学生的抽象素养，为促进学生核心素养的形成与发展奠定基础.

■ 抽象素养的培养措施

1. 注重情境创设

孔子曰：“不愤不启，不悱不发.”这句话着重强调教师的启发对教学的重要性. 数学知识本就源于生活，并应用于生活. 因此，教师可结合学生的生活经验，创设一些贴近学生生活的教学情境，以拉近数学与生活的距离，培养学生的抽象素养. 基于数学知识本身就具有高度的抽象性与逻辑性特点，教师更应关注情境的启发作用，使数学教学更具生活味.

案例1 “函数的概念”的教学.

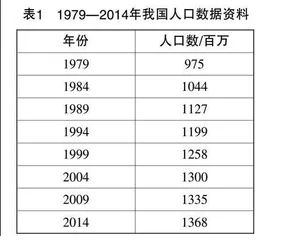
情境1：表1是1979—2014年我国人口数据资料，请根据资料说一说我国人口的变化情况.

情境2：如图1所示，观察通城三月份某天24小时的气温图，说说这天的最高气温、最低气温、什么时候的温度为0°、什么时间段的气温高于0°.

要求学生观察并思考上述两个情境具有哪些共同点，通过小组讨论的方式，尝试归纳函数的概念. 在讨论过程中，教师适时引导：将两个情境中的变量视为x，y，探索它们间存在怎样的对应关系.

经探索，学生自主获得结论：集合A中的x，可从对应关系出发，获得集合B中与之唯一对应的y. 根据这个结论，学生推导出函数的概念，确定y=f（x）的含义.

生活情境的创设引发学生思考，让学生在教师引导与合作交流中自主获得一些结论，形成函数的概念. 这种教学方式比教师直接呈现函数概念更容易让学生接受与理解，函数的概念由学生自主抽象而来，因此不论是记忆还是理解都更加深刻.

恰当的情境创设可降低学习难度，激发学生的探索欲，让学生在充满生活味的情境中积极探索新知，这是学生积累学习经验，提高学习效率的基本途径，也是培养学生抽象素养的重要手段.

2. 加强变式训练

变式训练是经过多轮教育改革后形成的一种重要教学方式，主要指从一般性问题出发解决探索性问题的过程. 在变式训练过程中，教师可将一些解决标准性问题的思维延伸到新的问题中，让学生通过问题的解决来了解知识间不断发展的关系，为灵活应用数学知识解决实际问题奠定基础.

通过变式训练提升学生的抽象素养可从精讲典型例题出发，让学生从数学抽象思路与方法上着手去合情推理，以确保抽象理论的准确性. 变式应用时应注重导向性、层次性与适时性原则. 拿层次性来说，变式训练应注意梯度分明、层次清晰且有合理的跨度，通过“低起点、密台阶”的策略实现学生的思维拾级而上.

案例2 “函数”的解题教学.

3. 深化知识应用

不少学生学习困难的主要原因在于不会灵活应用所学知识，函数作为教学的重中之重，对于学生而言确实比较抽象，想要从真正意义上掌握其应用，还要在日常多训练、勤积累，提升抽象素养.

知识的学习最终都是为了更好地为生活服务，鉴于数学知识大部分源于生活实际，因此应用教学应与学生的生活实际挂钩，用生活问题来深化学生对数学模型的理解.

案例3 “函数”的应用教学.

已知函数f（x）的边际函数Mf（x）定义为：Mf（x）=f（1+x）－f（x）.

报警系统装置公司每月最多可生产100台报警器，若生产x台（x∈N*）的收入情况为R（x）=3000x－20x2，成本函数为C（x）=500x+4000，利润为收入和成本的差.

问题：（1）分别求边际利润函数MP（x）与利润函数P（x）；

（2）分析MP（x）与P（x）是否存在相同的最大值.

解决本题可遵循“审读例题—建立模型—求解模型—实际解题”的流程，学生可在函数的概念与性质的基础上解题. 通过解题流程的感知，体验解决这一类问题的方法. 随着解题框架体系的建立，学生的抽象素养也相应得到提升，当再次遇到类似问题时，则能借助原有的认知经验解题.

总之，抽象素养的培养需经历一个长期、复杂的过程. 作为一线数学教师，应根据学情、教情与考情不断调整教学方案，带领学生全身心地投入到数学学习中去提升抽象素养，让数学学科核心素养落地生根.