基于历史名题的高中数学单元复习课教学：庞海燕

[摘  要] “阿基米德三角形”包含了直线与圆锥曲线相交、相切两种位置关系，聚焦了轨迹方程、定值、定点、弦长、面积等解析几何的核心问题，能够很好地体现“坐标法”的解题思想，揭示数形结合方法的本质. 圆锥曲线复习教学中存在着学生算理清楚、运算过程却难以推进和教师例题选择缺乏整体性的问题，为解决这两个问题，研究者以圆锥曲线中的“阿基米德三角形”为载体，开展“圆锥曲线的方程”单元复习教学研究. 实践表明：由“阿基米德三角形”引领的圆锥曲线单元复习课教学浸润了知识源流、学科联系、社会角色、审美娱乐、多元文化等维度的数学文化，深刻地揭示了数学史的六类教育价值.

[关键词] 阿基米德三角形;圆锥曲线;单元复习;历史名题;数学文化

[⇩] 引言

解析几何，是高中数学的重点与难点，而圆锥曲线是解析几何中的核心内容. “圆锥曲线的方程”是人教A版新教材高中数学选择性必修第一册的第三章内容，是“直线与圆的方程”的后续内容，主要运用“坐标法”探究圆锥曲线的几何特征，建立它们的方程，通过方程研究它们的性质，并解决与圆锥曲线有关的几何问题和实际问题，是对高中平面解析几何内容的深入学习和研究. 《普通高中数学课程标准（2017年版2020年修订）》指出：通过解析几何单元的学习，学生在平面直角坐标系中，运用平面解析几何方法解决简单的数学问题和实际问题，感悟平面几何中蕴含的数学思想，进一步体会数形结合思想[1].

在圆锥曲线单元教学实践中发现：一方面，学生通过新课学习熟悉了圆锥曲线的基础知识，但学生解题的方法零散，解决综合性问题的能力弱，往往由于运算烦琐经常算不下去，且解题后缺乏反思和总结;另一方面，教师由于课堂时间紧张，往往只讲解题的思路和方法，运算交给学生课后进行，缺乏解题示范和规律总结，缺少对整体性、系统性知识方法的有效建构.

数学历史名题，是指在数学演进的历史长河中，对数学发展、社会应用、科学进步等方面产生一定影响的数学问题，展现数学文化的多元内涵.

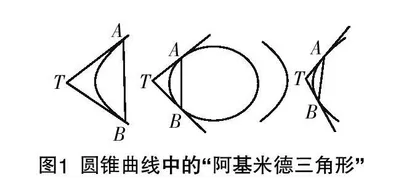
过圆锥曲线的弦两端的切线与弦所围成的三角形被称为该圆锥曲线的“阿基米德三角形”（见图1）. 据说，古希腊数学家阿基米德（Archimedes，公元前287年—公元前212）在其著作《抛物弓形求积》中提出了一个用三角形穷竭抛物线弓形面积的算法，解决了抛物线弓形面积问题，其中衍生出了“阿基米德三角形”，具有相当多的优美性质. “阿基米德三角形”包含了直线与圆锥曲线相交、相切两种位置关系，聚焦了轨迹方程、定值、定点、弦长、面积等解析几何的核心问题，“坐标法”的解题思想和数形结合方法的优势体现得淋漓尽致，更能在课堂上提升学生解决圆锥曲线问题的能力，落实逻辑推理、数学抽象、数学运算等核心素养.

鉴于此，本研究基于“阿基米德三角形”这一历史名题，开展圆锥曲线单元复习教学研究，拟定教学目标如下：

（1）通过“坐标法”解决直线与圆锥曲线中线段长度问题、轨迹问题、切线问题、最值问题、面积问题等，掌握“应用定义”“应用判别式”“运用向量工具”“运用平面几何知识简化”“数形转化”“与导数结合”6个方面的解题策略，体会数形结合、转化与化归的思想方法.

（2）经历从特殊的“阿基米德三角形”到一般情形的过程，提升学生类比、迁移和抽象的能力;经历从一般情形中发现特殊的“阿基米德三角形”的过程，培育学生发现问题、分析和解决问题的能力.

（3）了解“阿基米德三角形”问题的历史演进过程，培育学生的动态数学观，培育学生的理性精神，让其品味精彩的数学文化.

[⇩] 史料运用

1. 史料简析

古希腊数学家阿基米德在其著作《抛物弓形求积》中利用一系列内接三角形逐步逼近抛物线弓形，借助于“穷竭法”解决了抛物线弓形的面积问题（见图2）. 设AB是抛物线的一条弦，阿基米德证明[2]：

命题1：过抛物线上任意一点P作抛物线对称轴的平行线，交AB于点C，若AB平行于抛物线在点P处的切线MN，则AC=BC;反之，若AC=BC，则AB平行于抛物线在点P处的切线MN.

命题2：P为抛物线上任意一点，直线AB与抛物线在P处的切线MN平行，交抛物线于点A和B，过P作抛物线对称轴的平行线，交AB于点C，交抛物线在点A处的切线于点T，则PT=PC.

命题3：过AB的中点C作抛物线对称轴的平行线，交抛物线于点P，则P为抛物线弓形的顶点.

命题4：设P是抛物线弓形ABP的顶点，Q和R分别是AP和BP所截的小抛物线弓形的顶点，则S=S=S.

命题5：设P是抛物线弓形的顶点，则抛物线弓形ABP的面积等于S.

阿基米德通过命题4得到了S+S=S，继续对小弓形进行了类似的分割，其后的三角形也有同样的面积关系. 抛物线弓形ABP的面积可以用所有这些内接三角形的面积和来“穷竭”，也就是可以用几何级数S+S+S+…的有限项之和逼近，其中S=S[3].

2. 史料融入单元复习课教学的方式

由“阿基米德三角形”引领的圆锥曲线单元复习课例中，采用了数学史融入数学教学的4种方式，具体如下：

（1）附加式. 活动1“发现者：数学构件——基本性质研究”中以“微视频”的形式介绍阿基米德对抛物线弓形面积的研究方法与积极贡献，活动2“创造者：数学建构——轨迹探寻”中对“蒙日圆”的介绍，引导学生感悟精彩的数学文化.

（2）复制式. 情境创设环节引入“阿基米德三角形”的定义，引导学生重走数学家研究之路，激发学生的学习热情、探究兴趣.

（3）顺应式. 活动1中利用命题4、命题5设计Q4，以及引导学生自己思考解决抛物线弓形面积的方法，在从特殊到一般情形的过程中，提升学生类比、迁移和抽象的能力.

（4）重构式. 活动3“探究者：数学应用——一般问题探究及溯源”中通过Q6、Q7引导学生发现一般情形中的“阿基米德三角形”，培育学生发现问题、分析和解决问题的能力.

依据“阿基米德三角形”相关的历史名题来梳理高三单元复习课中的解题规律，化解机械化计算的枯燥. 通过分析问题、解决问题，引导学生利用类比法探究直线与圆锥曲线的位置关系问题的本质，认识到问题背后的规律性，抽象出数学解题过程.

[⇩] 教学实践

1. 创设情境

课前提前发放《预习单》，引导学生分析和解决问题，洞察问题之间的紧密联系，为后续复习做好铺垫.

Q1（教材P136，例5）：经过抛物线焦点F的直线交抛物线于A，B两点，经过点A和抛物线顶点的直线交抛物线的准线于点D，求证：直线DB平行于抛物线的对称轴.

Q2（教材P138，复习巩固，第6题）：如图3所示，直线y=x-2与抛物线y2=2x相交于A，B两点，求证：OA⊥OB.

Q3（教材P139，拓广探索，第12题）：已知抛物线的方程为y2=4x，直线l绕点P（-2，1）旋转，讨论直线l与抛物线y2=4x的公共点的个数，并回答下列问题：（1）画出图形表示直线l与抛物线的各种位置关系，从图中你发现直线l与抛物线只有一个公共点时是什么情况？（2）y2=4x与直线l的方程组成的方程组的解的个数与公共点的个数是什么关系？

教师引导学生分析并发现《预习单》中Q1至Q3的共性——直线与圆锥曲线相交或相切. 以Q3中的抛物线为例，过抛物线外一点P作抛物线的两条切线PA，PB，连接AB，得到△PAB. 在△PAB中，PA，PB是抛物线的切线，AB是抛物线的一条弦，聚焦了相交、相切两个问题. 教师介绍“早在两千多年前，数学家阿基米德就用几何论证、物理方法对这个三角形开展过系列研究”，以“这个三角形究竟有什么神奇之处”“阿基米德又做了哪些工作”等问题激疑，展开对“阿基米德三角形”性质的深入探究.

2. 课堂探究

活动1从最简单、最特殊的情况——抛物线的焦点弦开始，从点的坐标、直线的方程到弦长、三角形的面积，这些对学生来说，都属于熟悉的数学问题情境.通过对其研究，引导学生能够在熟悉的情境中直接抽象出圆锥曲线中的切线问题、切点连线、轨迹问题、线段长度、面积及最值问题的解决方法，明晰算理，并类比、迁移到一般情形，引导学生发现、探究、欣赏与“阿基米德三角形”相关的数学历史名题.

【活动1】 发现者：数学构件——基本性质研究.

Q4：已知抛物线x2=4y的焦点为F，A，B是抛物线上的两动点，且=λ（λ>0），过A，B两点分别作抛物线的切线，设其交点为M（如图4所示）.

（1）证明：M在抛物线的准线上;

（2）证明：·为定值;

（3）证明：MA⊥MB;

（4）证明：若AB的中点为C，则MC∥y轴;

（5）求解：设△ABM的面积为S，写出S=f（λ）的表达式，并求S的最小值;

（6）过AN的中点D作DE∥y轴，交抛物线于E，证明：S=8S.

其中，Q4（4）对应命题2，Q4（5），Q4（6）对应命题5.

利用“坐标法”完成解答后，进行题后反思.

师：在Q4（1）中，整理切线MA的方程y=x-y，得到MA：xx=2（y+y）. 这个方程的形式具有什么代数特点？若结合M的坐标和AB的方程，又有什么代数特点？可以推广到一般的情形吗？请小组合作，研讨记录.

对学生研讨的内容进行梳理，得出结论：对于抛物线y2=2px（p>0），若点P（x，y）在抛物线上，则直线yy=p（x+x）为点P（x，y）处抛物线的切线方程;若点P（x，y）在抛物线外，则直线yy=p（x+x）为P（x，y）对应的两条切线的切点连线的方程.

教师指出：圆、椭圆、双曲线也都有类似结论.

师：结合Q4（1）、Q4（3），思考两条切线的交点具有什么几何特性.

学生再次小组讨论，得出结论：两条切线的交点在定直线上.

师：Q4（4）的逆命题成立吗？即若AB的中点为C，M在抛物线x2=4y的准线上，且MC∥y轴，则MA，MB是抛物线的切线吗？若成立，这个命题会给我们带来什么启示？

生：只需验证M

，-1

是否满足方程xx=2（y+y），这显然成立！这个结论将启示我们：作抛物线的切线，它不再是“看得见却摸不着”了！

师：Q4中的直线AB是过抛物线焦点的，如果改变这个条件，比如说直线AB过点（0，2），类比前面的解答过程，哪些步骤会有影响？结论会有影响吗？

学生结合演算过程验证自己的想法.

教师播放与阿基米德相关的微课视频，主要内容是阿基米德的主要研究工作、抛物线弓形面积的算法（如图5所示）.

师：对比阿基米德的想法，我们通过对Q4（6）的研究，可以推出弓形AOB的面积吗？

生：过BN的中点G作GH∥y轴，交抛物线于H，所以S=8S，从而S+S=S，重复这一过程，利用无限个小三角形逼近弓形ABN的思想，得S=S+S+S+…=S.

【活动2】 创造者：数学建构——轨迹探寻.

接着，活动2安排了椭圆两条切线相交产生的交点轨迹问题，帮助解决绝大多数学生不能有效表征的问题，以及知道算理却算不下去的问题. 跳出抛物线，引导学生用类比法了解椭圆等其他背景中的“阿基米德三角形”的性质，以及解决以此为背景的问题.在研究椭圆的两条切线的交点的过程中，让学生创造发现另一个历史名题——“蒙日圆”，引导学生深切地感受研究的乐趣，浸润多元数学文化的芬芳！