素养导向的学科实践：思维可视化的实现路径

[摘 要] 20多年的数学课程改革，“满堂灌”的课堂形态得到较大改变，但虚假探究现象仍较突出。新课改要求学生以实践的方式进行学科学习，展现思维的过程与结果，让“探究”迭代升级。数学学科实践是实现思维可视化的路径之一，思维可视化助力数学学科实践育人价值的彰显。基于对课标、教材、学情的准确把握，多样实践形式让思维“看得见”“看得清”“看得远”。围绕问题解决，以问题解决为导向，构建真实有意义的情境，激活学生认知及探究的心理，引导学生经历问题表征、策略探究、方法迁移、模型构建等可视化过程，发展数学思维素养。数学学科实践并不是数学学习的唯一方式，应根据学习内容与学习对象特点灵活选择多种学习方式，合理进行思维可视化，发展学生核心素养，实现学科育人功能。

[关键词] 核心素养；学科实践；实践育人；思维可视化；数学学科特质

[中图分类号] G64    [文献标识码] A   [文章编号] 1005-4634（2024）05-0086-07

数学课程改革已实施了20多年，课改突出综合实践活动的“实践”功能，“自主、合作、探究”学习方式的普遍运用，使“满堂灌”的课堂形态得到较大改变。但是，数学学科实践基本上还是项目式学习或主题活动形式，“为探究而探究”的“虚”“假”“泛”“浅”“僵”现象仍较突出，无法从根本上促进学生“像专家一样思考与行动”、用“学科的方法”获得并实践“学科知识”，实现知行合一和自我建构。2022年，《义务教育课程方案和课程标准（2022年版）》正式实施，要求将“实践”融入到各学科课程学习中，促使“自主、合作、探究”迭代升级，以实践的方式进行学科学习，展现思维的过程与结果，提升学生思维能力与动手操作能力，将学科实践转化为学科素养。

从学科特性出发，以学科独有的方式学习，以学科实践落实学科育人，培育学生综合素养，是学科实践的出发点与归宿。数学学科实践离不开思维参与，以独特的思维方式解决数学问题，使数学知识转向数学素养发展。“鸡兔同笼”是经典的数学问题，多种版本教材均安排了此内容。人教版安排在四年级下册“数学广角”探究活动中，主要目的是让学生经历自主探索问题的解决过程，呈现思维历程，理解列表、画图、假设法，在学科实践中渗透数学思想与方法，发展学生数学核心素养。下面以“鸡兔同笼”教学为例，探讨如何在学科实践中发展学生思维能力。

1 数学学科实践、思维可视化的逻辑关系

1.1 数学学科实践的内涵

20世纪50年代，施瓦布（Schwab J J）在亚里士多德、杜威等人思想的基础上提出并发展了实践课程概念，认为实践课程具有“真实性、探究性、过程性与情境性”等特点 [1]，驱动着对学科实践内涵的重构。“学科实践”是针对真实情境中的特定问题，运用具有学科特点的做法，让学生像专家一样，通过动手和动脑亲身体验探究的过程 [2]。传统的学习方式多为记忆、练习、理解、思考等，本次课程改革，将从根本上改变传统的“坐而论道”等育人方式，强化行动、体验、感悟、思维、创造等多样学习形态。杜威的名言“教之于学犹如卖之于买”，阐明了将书本知识转化为学生的知识的重要性。只有亲身经历知识产生的历程，让知识在“基于实践、通过实践、为了实践”的过程中产生、应用与发展，才能使“学了”变成“学会了”，才可能将书本知识变为学生的知识。学科实践不仅可以使学生学习和运用新知识，而且能促进其综合素质的发展 [3]。

数学学科实践是以数学学科知识学习为基础，以真实问题情境和高阶思维参与为基本特征，围绕数学问题解决，以发展学生数学眼光、数学思维、数学语言为目的的实践学习方式，也是一种对知识的理解、探究和创造的数学学习活动。数学学科实践样式包括但不仅限于综合与实践活动课程，一般包括以探索发现为目标的数学问题探究、以验证理解为目标的数学实验操作、以综合应用为目标的主题活动或项目活动3种基本样式。数学探究性学习从本质上说是一种数学学科实践形式。加拿大不列颠哥伦比亚省课程改革，设置了各个学科的实践方式，其中数学实践包括“推理和分析”（reasoning and analyzing）、“理解和解决”（understanding and solving）、“沟通和表征”（communicating and representing）、“联系和反思”（connecting and reflecting）。“鸡兔同笼”问题，具有较强的探究性，让学生亲身经历“假设—比较—调整”的问题解决的过程，能够积累数学经验，训练思维能力，发展数学运算、逻辑推理、直观想象、数学建模等核心素养。

1.2 思维可视化的内涵

思维可视化，是“让思维可见”，以恰当的操作活动（如直观语言、图式表征、动作操作等），将“看不见，摸不着”的思维，变得“看得见，摸得着”，让他人能看得见自己的思考路径，让自己看得见思维的影响，从而促进思维成长。约翰·哈蒂提出了 “可见的学习”核心概念，当 “可见”发生时，对学生学习产生的效应最大 [4]。 根据活动理论内化和外化结合的原则，学科实践活动有将学生个体的认知转化为外在行为的外化过程，改变着学生的学习方式。因而，学科实践活动是由内化转向外化，再由外化影响内化的过程。思维可视化，是小学数学深度学习的典型特征。借助思维外显手段，有利于将抽象的数学知识具象化，把内隐的思维过程外显化，实现“内”思考与“外”表现的转化，激发学生主动思考的意识与活力，实现真正的深度学习。“鸡兔同笼”课堂学习，借助简单的图形、表格等表征形式，记录了猜想的过程，留下了思考的痕迹，呈现多种列表方法，发展了学生思维的灵活性、独创性。

1.3 数学学科实践与思维可视化的关系

1.3.1 数学学科实践是实现思维可视化的路径之一

数学学科实践的本质要求是用数学独特的方式学习数学，是基于数学学科特点，体现数学学科思想和数学方法，彰显数学意蕴的学习方式。没有思维参与的实践不是数学实践。数学学科实践以问题探究为核心，思维过程与思维形式则是问题探究的内在逻辑和最终追求 [5]60 。再现与描述思维过程和思维形式，即是思维可视化的过程。数学学科实践能引发学生数学思考，用数学的思维方式方法发现问题与解决问题，并形成清晰的数学逻辑思路，用恰当的形式将思考过程表现出来并与他人交流，实现了思维的可视化。“鸡兔同笼”教学将学生带入古今对同一问题解决方法的差异化情境中，引导学生用已有的知识与经验进行猜想、验证，经历列表有序思考—绘图数形结合—运算验证等实践操作过程，以列表、画图、算式等方式将思考过程可视化，实现了“学科实践”与“思维可视化”的巧妙结合，学生的知识体系得到了自主建构。

1.3.2 思维可视化彰显数学学科实践育人价值

根据多维学习理论，借用数学符号、图形、文字语言或者动作等表达数学实践过程与结果，让学习过程外显、情境可视，学生必定能得到全新的心理体验，激发多种感官参与，促进“四基”“四能”发展，形成正确的情感、态度和价值观。

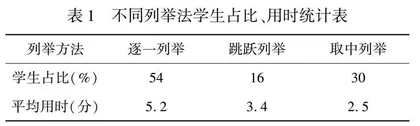
数学学科实践结果相同，并不等于思维过程一致。问题解决方法的多样性，取决于思维方式的多样性。学生在用列表法解决“从上面看有8个头，从下面数有26只脚，鸡兔各有几只”问题时，在得出“鸡3只、兔5只”正确答案的学生中，所用方法与时间统计见表1。

由此可见，学生虽都用列举方法得到了正确答案，但思维过程有异，用时也有较大差异。针对几种列举法，教师引导学生结合“添足”或“抬脚”画图法，进行对比分析，沟通了列举与假设法的关系，深刻理解了假设法的本质，进一步彰显了分享活动前学生自主探究实践活动的价值。

多样的思维可视化方式，优化了实践操作过程。“画出来”“写出来”“说出来”更能推进“做”得更好。在解决“鸡兔同笼”的问题时，教师请8位学生到台上扮演鸡和兔，尝试有26只脚在地，提出问题：“需要有几位学生扮演鸡或兔？”经过讨论，有5位学生自然将“手”扮为兔足。他们既能表演出装扮的过程，也能描述为什么这样装扮，“所说”即“所想”，以“说”的方式表达“想”和“做”的过程。当头不变（学生人数不变）时，探究如何调整“足”的数量，降低了实践操作难度，也优化了操作过程。

学科实践包含了多种思维可视化方式，正确应用能有效地促进学生思维的生长与发展，提升学生的数学素养。

2 基于思维可视化的学科实践路径建构

2.1 指向思维可视化的学科实践设计起点：基于课标、教材、学情分析

新课程标准要求强化“做中学”，“做”让思维“看得见”。引导学生参与数学学科探究活动，经历发现问题、解决问题、建构知识、运用知识的过程，体会数学思想与方法，提升解决真实问题的能力。人教版小学数学教材“数学广角”，从学生日常生活中选材，如路灯安装、花坛摆花、道路旁植树、沏茶、烙饼等，在实际生活问题的解决过程中渗透数学思想与思维方法；有部分内容增加了阅读资料，介绍了有关数学知识，渗透了数学文化，如古代的数学问题“鸡兔同笼”等。“数学广角”突出在数学操作中进行数学思考，在可见的活动中学习。如在“找搭档”游戏中思考排列组合，在“田忌赛马”过程中思考数学优化，在探究“鸡兔”各多少只的活动中体会假设法的应用等，在具体探究实践过程中形成理性思维。

对于“鸡兔同笼”的教学内容，不同版本教材编排年级、体例、呈现的问题解决方法有别，表2为各版本教材“鸡兔同笼”问题分布情况及解决方法。

“列举”让思维“看得清”。9种教材都把此内容作为独立的学习主题，呈现了“列举法”这种基本的问题解决策略，体现了“猜想—比较—推理—调整”探究过程。人教版（2014）将内容安排在四年级下学期，以列表比较、画图表征为基本特征的“可视化”平台，使学生在具体的“猜想—比较—调整”过程中感受“鸡兔”头与脚数量的变化规律，深度理解抽象的“假设法”的本质（列举法与画图法都体现不同层次的假设思想）。

“假设”思想分学段渗透，让想象思维逐渐“看得远”。用列表假设法进行实践探究，是用数学学科特有的方式进行活动，有鲜明学科实践的特点。假设是一种预见与猜想，是有意义的高阶思维，也是一种问题解决的重要思想方法。小学阶段，基本上是在具体真实的情境中假设，假设的过程与结果常以具体的图像、图表、符号、数值等方式表达，是一种具体化的假设，是在数学学科实践活动中假设。学生从一到六年级数学学习过程中贯穿了“假设法”或假设的思想，表3为学生在各学段运用假设法的情况。

由此可见，学生从一年级开始接触假设法，但很隐蔽。假设法与具体操作结合，用图表、算式等方式表达假设法的过程，将抽象的推理转化为便于理解的具象，由图表到抽象的符号，层层递进。

九种教材中，人教版教材最早安排“鸡兔同笼”假设法解决问题，并以此构建问题模型思想。四年级是一个承上启下的过渡年级，虽然学生的逻辑思维能力不断发展，推理意识逐渐增强，但是形象思维在问题解决中仍占有重要地位。调查发现，在课堂学习前，有近30%的学生以“试”“猜”的方法找到数字较小的“鸡兔同笼”问题的正确答案，能找到数字稍大的“鸡兔同笼”问题的人数仅为10%左右。由此表明，“试”也有方法，盲目地“试”对复杂问题的解决作用不大。学生需要在不断猜测中获得确定的规律，应用规律解决问题，实现“不试”或科学地“试”。“鸡兔同笼”的学习，使学生借助列表特例进行尝试与探究，发现隐含的替换规律，明确“画图”“列举”“假设”等方法间的内在联系，进而真正理解假设法原理，推动思维发展。

2.2 围绕数学问题解决：基于思维可视化的数学学科实践的实施路径