新教材下“10的认识”教学重构

摘  要：对“10的认识”，苏教版小学数学新教材编写变化的核心是，根据新课标理念，强调在十进位值制记数法的基础上认识10。因为十进位值制记数法蕴含按群计数的整体思想、位值记数的直观思想，是小学阶段认识整数、

小数以及进行相应的计算时起到统领、迁移作用的大概念。根据新教材的变化，“10的认识”的教学应该突出计数单位和数位，建构十进位值制记数法基石。具体地，要注意：基于数位的建构，理解自然数10的写法；基于计数标准的改变，建立计数单位“十”；应用“满十进一”，凸显10的计算价值。

关键词：小学数学；新教材；10的认识；计数单位；数位

一、从新教材的变化谈起

数是对数量的抽象，记数是对数的符号化表达。数的认识是经历由数量到数的抽象并根据记数规则建构数的意义的过程。作为起点，10以内数的认识是一年级上学期数学教学的重要内容。对这部分内容，根据《义务教育数学课程标准（2022年版）》（以下简称“新课标”）编写的苏教版小学数学教材（以下简称“新教材”），相比于根据《义务教育数学课程标准（2011年版）》编写的苏教版小学数学教材，做了较大的调整：将《认识10以内的数》《分与合》《10以内的加法和减法》三个单元重新组合拆分成《0—5的认识和加减法》《6—9的认识和加减法》《10的认识和加减法》三个单元。

这样调整，一方面，加强了数与运算的联系——新课标指出：“数的认识与数的运算具有密切的联系，（教学中）既要注重各自的特征，也要关注二者的联系。”［1］另一方面，凸显了10的特殊性与重要性——新课标指出：“10以内数（的认识）的教学重点是，使学生体验1—9从数量到数的抽象过程，通过9再加1就是十，体会十的表达与1—9的不同是在新的位置上写1，这个位置叫十位，十位上的1表示1个十，1个十用数字符号10表达。”［2］

聚焦“10的认识”，通过比较不难发现：虽然两版教材都以生活情境中的10个一组引入，蕴含按群计数的思想，但是，旧教材着力于认识自然数10，只是在练习中通过“10根小棒捆成一捆”让学生初步感知计数单位“十”（直到《认识11—20各数》单元才让学生进一步认识“10个一是1个十”等），而新教材将自然数10的认识和计数单位“十”的认识融为一体，强调10和以前学的数的不同，借助小方块等让学生理解“10个一是1个十”和计数单位的作用，巧用计数器让学生理解“满十进一”和数位的作用。

进一步分析新教材的编写，可以发现以下立意。（1）以计数方式为主线串联对计数结果10和计数单位“十”的认识。以“一”计数得到结果10（作为整体的符号记录并记忆）自然过渡到以“十”计数建立单位“十”，凸显认识的整体性与思维的连贯性。（2）以计数工具为载体建构对计数单位“十”的认知。利用手帕纸、小方块、计数器、数轴等工具，通过实物和图像等表征方式，帮助学生丰富表象，打破对计数单位“一”的认知惯性，确立计数单位“十”的概念。（3）以对比思辨为抓手强化对位值原理的感悟。引导学生思考：10和以前认识的数有什么不一样？基于在计数器上拨数的体验，学生可以认识到：10是一个两位数，没有用新的数字表示，而是将1和0放在不同的位置上来表示，1和0分别表示1个十和0个一。由此认识数位和数位上的数字，感悟位值原理。

二、10的教学价值再认识

新教材变化的核心是，根据新课标理念，强调在十进位值制记数法的基础上认识10。十进位值制记数法蕴含重要的数学思想，比如按群计数（计数单位）的整体思想、

位值记数（数位）的直观思想［3］，是小学阶段认识整数、小数以及进行相应的计算时起到统领、迁移作用的大概念，应该从认识最小的两位数10开始建构。因此，10有着重要的教学价值：作为起点，体现十进位值制记数法蕴含的数学思想，建构十进位值制记数法基石。这里，做进一步的分析：

（一）整体的计数单位：从逐一计数到按群计数

学生以逐一计数开启他们的数学学习与应用，认识10时首次接触基于十进制的按群计数法。其实，在现实生活中，按群计数随处可见，如每6颗珠子串成一串、每8颗糖装成一盒等。但是，这些只是生活现象，具有临时性和可变性，学生还没有从数学的角度产生按群计数的抽象认知。因而，从按“一”计数到按“十”计数，是一次全新的认知建构，是认数历程中一次重要的跨越。“十”作为十进制下按群计数的约定标准，“按”下了以数群的方式计数的“键”，并可以迁移建立百、千、万等更大计数群（单位）以及更小的计数体（单位）。同时，按群计数思想也为今后接触（学习）二进制、八进制等其他进制计数法提供了思考建构的支架。

（二）直观的数位：从有限的数字到无限的数

10是自然数建立“满十进一”记数规则的首次表达。从10开始，不仅有了可以不断生成的新的计数单位，而且有了计数单位的直观表达——数位。由此，面对任何记数的需求，都可以不使用新的数字符号，而使用之前的0—9这十个符号在不同的数位上表达新的数。0—9这十个数字加上位值原理，构成了一套简洁、完整的记数方法（系统），能够实现用有限的数字符号表示出无限的数。这种突破性的记数方法是人类的伟大创造：如果没有直观的位值原理，记数时就需要不断产生新的数字符号（表示新的个数或新的计数单位），这必然带来极大的不便。

三、“10的认识”教学过程再设计

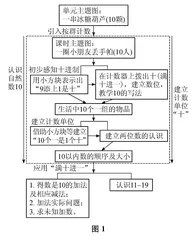
根据新教材的变化，“10的认识”的教学应该突出计数单位和数位，建构十进位值制记数法基石。大致教学过程如图1所示。

图1

（一）基于数位的建构，理解自然数10的写法

学习知识在很大程度上是通过符号探索意义世界，在实质上就是理解与把握符号所表达的意义。［4］入学前，学生对10的认识就是一个（整体的）符号，没有数位的概念。10为什么这样写？为什么不像0—9那样有专属的符号？这些都是学生潜藏的疑问。这些疑问只有在数位概念建立起来后，才能得到解决。数位是抽象的、无形的，学生认识数位是有难度的，因此，需要借助计数器直观表达与展现。

教学中，可以组织学生在计数器上拨出10以内的数，先确立个位（不出现十位）。当学生在个位上拨出10时，可以让他们尝试继续拨出下一个数。学生会发现：计数器个位上只有10颗珠子，无法在这一位继续拨出下一个数。为什么计数器个位上只有10颗珠子？怎样在计数器上拨出比10大的数？在这些疑问中，教师引导学生想办法让10颗珠子“搬家”，只用1颗珠子在新的位置上表示10，从而将个位空出来，使得在个位上可以继续拨出下一个数。这样，激发学生“满十进一”的需求，引导学生创造出新的数位——十位。

数位建立后，10的写法就可以建立在意义理解的基础上。教学中，可以引导学生思考以下问题：（1）大家都会写10，联系计数器，想一想10为什么这样写？（2）想一想个位上的1和十位上的1表示的意义相同吗？为什么？（3）个位上的0可以不写吗？讨论这些问题，有助于学生深度理解十进位值制记数法的位值原理，包括0的占位功能。

此外，教学中还要组织学生结合拨珠的经验讨论10与一位数的区别，体会：一位数由一个数字构成，在个位上计数；10是两位数，需要用1和0两个数字分别在十位和个位上表示。

（二）基于计数标准的改变，建立计数单位“十”

从以“一”计数走向以“十”计数，即改变计数标准，从另一个角度诠释数的组成，对学生的认知是一个挑战。教学中，要依据学生的思维水平，组织学生具身学习，在观察、操作、感悟、表达中，理解新的计数单位“十”，打通新旧计数单位之间联系。

首先，要帮助学生读懂教材中的主题图。教材中从单元主题图到课时主题图，做了很多伏笔：一串冰糖葫芦是已经串上的9颗加即将串上的1颗得到的10颗，一圈小朋友是坐着的9个加站着丢手帕的1个得到的10个。这里，10都是作为一个整体出现的。教学中，要强化这一计数标准，可结合主题图提问：一串几颗？一圈几人？从而调整学生计数的视角，孕伏按群计数的思想。

其次，要组织学生开展丰富的操作活动。教材中两次出现用小方块计数：第一次是用小方块表示出主题图中的人，小方块与人是一一对应的，在边摆边数的过程中体会10是由“一”这个单位累加的结果，“逐次添1”是得到新的自然数的基本方法；第二次是把10个小方块聚拢变成1条小方块，直观表示出10个一变成1个十的过程。教学中，可以结合10个一组的物体（如手帕纸、铅笔等）以及计数器十位上的1颗珠子，让学生移一移把10个小方块变成一个整体，想一想“变化前有几个一，变化后成为几个十？由此能想到什么”，再通过交流，把操作过程中的感悟提炼成计数单位之间的联系。还可以让学生回顾10个一组物体的形成过程和计数器从个位上的10颗珠子到十位上的1颗珠子的过程，找一找“10个一是1个十”，建立丰富的表象。

此外，还可以让学生联系生活，找一找或摆一摆生活中的“10个一是1个十”，如：10个硬币是10个一，摞起来就是1个十；10个鸡蛋是10个一，放进一个盒子里就是1个十……通过举例与解说，不断诠释对“10个一是1个十”的理解，让思维走向深处。

（三）应用“满十进一”，凸显10的计算价值

法国数学家拉普拉斯曾经这样赞美位值记数：“用10个记号表示一切数，每个记号不但有绝对的值，而且有位置的值，这是深远而又重要的思想。它今天看来如此简单，以至于我们忽视了它的真正伟绩。但恰恰是它的简单性以及给一切计算都带来极大的方便，才使得我们的算术在一切有用的发明中列在首位。”

数的认识是数的运算的基础，通过数的运算有助于学生更好地认识数。认识自然数10时，学生首次建立数位的概念：10是个位“满十进一”到十位的记数结果。凑十法、破十法、平十法等都是基于10的计算价值产生的，由此建构20以内进位加和退位减的算理与算法，形成所有整数加法和减法的计算基础。因而，本单元在“10的认识”后，趁热打铁安排了相应的计算教学：3课时加减法计算及相应的解决问题、1课时综合与实践活动，分别为“得数是10的加法及相应的减法”“加法实际问题”“求未知加数”和“好玩的‘抢10’”。以“求未知加数”为例，教学内容蕴含函数思想，例题呈现了一个10格的木盒，盒子里放着8个桃，围绕问题“再放几个是10个”，列出含有未知加数的式子“8+（  ）=10”。学生可以选择看图观察、按序数数、想加算减等多种方法求得括号里的加数。求未知加数的过程是20以内进位加凑十法的重要步骤。“求未知加数”的教学巩固了10的认识，夯实了十进位值制记数法的基础，为后续的计算教学做好了铺垫、搭好了梯子。

参考文献：

［1］［2］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：20，20.

［3］ 卜俊.在计数与记数活动中体会数学思想——《认识11—20各数》教学与思考［J］.教育研究与评论（小学教育教学），2022（12）：8084.

［4］ 张华.让学生创造着长大——2022年版义务教育课程方案和课程标准核心理念解析［M］.北京：教育科学出版社，2022：68.