“结构化”与“层次性”
作者: 杨黎琴
摘 要:教学《正比例的意义》一课时,从学生熟悉的生活情境入手,引入一组具有结构化特征的实验,引导学生在比较与归纳中,基于“两种相关联的量”建立正比例的概念;进而设计一组层次性练习,帮助学生在迁移与运用中把握正比例的本质,由此促进学生对正比例意义的深度理解。
关键词:小学数学;《正比例的意义》;数学实验;结构化;层次性练习
“正比例的意义”是苏教版小学数学六年级下册第六单元第一课时的内容。学习这一内容时,学生对“判断有具体数据的两个量是否成正比例”容易掌握,而对“离开具体数据,判断两个量是否成正比例”较难掌握。因此,笔者在教学中,基于“做数学”的理念,从学生熟悉的生活情境入手,引入一组具有结构化特征(相互关联)的实验,引导学生在比较与归纳中,基于“两种相关联的量”建立正比例的概念;进而设计一组层次性(逐层递进)练习,帮助学生在迁移与运用中把握正比例的本质,由此促进学生对正比例意义的深度理解。下面分环节呈现本节课的教学过程与相应的教学思考。
一、在生活情境中感知“两种相关联的量”
师 (出示情境图)仔细观察屏幕上的信息,你有什么想说的?
生 数学书的单价是5.8元。
师 告诉我们的是数学书的单价,你联想到哪两种量?
生 我联想到总价和数量。
师 继续看动态演示,你发现了什么?
生 我发现,数学书的数量发生变化,总价也随着发生变化。
师 我们通常就说数量和总价是两种相关联量。你还能从生活中找到两种相关联的量吗?
生 汽车在高速公路上行驶,它行驶的时间和路程是两种相关联的量。
……
师 同学们举的例子都不错,老师也来举一个。老师的年龄和身高是两种相关联的量吗?
生 不是。
师
身高不会一直随着年龄的变化而变化,所以,年龄和身高不是两种相关联的量。
[思考:选择学生熟悉的数学书价格情境,激活学生关于单价、数量、总价关系的学习经验;通过具体数量和总价数据的动态演示,让学生直观感知“两种相关联的量”。“两种相关联的量”作为上位概念,是合适的“先行组织者”,为学习“正比例关系”奠定基础。]
二、在数学实验中寻找“两种相关联的量”
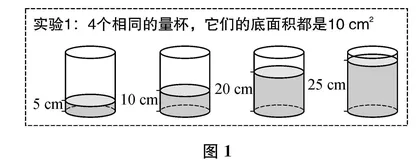
师 同学们,下面我们来做一组实验。(出示图1)
这是第一个实验,从中你能找到两种相关联的量吗?
图1
生 水的高度和水的体积是两种相关联的量。水的高度在变化,水的体积也随着在变化。
师 那它们到底是怎么变化的呢?(出示
表1)
请先填写表格。
表1 水的体积随水的高度变化的情况
水的高度/cm
水的体积/mL
(学生填表,交流。)
生 高度变高,体积也随着变大;高度变矮,体积也随着变小。
师 (出示图2)第二个实验是怎么操作的?从中你能找到哪两种相关联的量?
图2
生 石子的体积和总体积是两种相关联的量。石子的体积在变化,总体积也随着在变化。
师 那它们又是怎么变化的呢?
(学生填写表2,交流。)
表2 总体积随石子的体积变化的情况
石子的体积/cm3
总体积/mL
生 石子的体积变大,总体积也随着变大;石子的体积变小,总体积也随着变小。
师 (出示图3)这个实验又是怎么操作的?你找到两种相关联的量了吗?
图3
生 水的底面积和水的高度是两种相关联的量。水的底面积在变化,水的高度也随着在变化。
师 这两种相关联的量是怎么变化的?
(学生填写表3,交流。)
表3 水的高度随水的底面积变化的情况
水的底面积/cm2
水的高度/cm
生 底面积变大,高度随着变小;底面积变小,高度随着变大。
师 (出示图4)这个实验又是怎么操作的?又有哪两种相关联的量呢?
图4
生 水的底面积和水的体积是两种相关联的量。水的底面积在变化,水的体积也随着在变化。
师 具体来说呢?
(学生填写表4,交流。)
表4 水的体积随水的底面积变化的情况
水的底面积/cm2
水的体积/mL
生 底面积变大,体积也随着变大;底面积变小,体积也随着变小。
[思考:引入有趣的量杯盛水数学实验,让学生进一步循理寻找“两种相关联的量”,归纳发现变化规律,增强学习体验。同时,这组实验具有结构化特征,可以引发比较,让学生进一步认识到“两种相关联的量”之间可能有的不同关系,进一步为理解“正比例关系”做好准备。]
三、在比较归纳中建立正比例的概念
师 (出示图5)老师把4个实验的数据表格汇总在一起并做了点加工,请仔细观察表中数据,把4个实验中的“两种相关联的量”分分类。
实验1
水的高度/cm5102025
水的体积/mL50100200250
实验2
石子的体积/cm3581015
总体积/mL55586065
实验3
水的底面积/cm210203010
水的高度/cm60302015
实验4
水的底面积/cm210203040
水的体积/mL60120180240
图5
(学生小组讨论。)
师 你把它们分为了几类?分类的依据是什么?
生 两类:一类是两个量变化方向相同,另一类是两个变化方向不同。
师 好的,你是把实验1、2、4分为一类,把实验3分为另一类,对吧?那还有不同的分法吗?
生 3类。进一步把“两个量变化方向相同”这一类分成两类:实验1、4一类,实验2另一类。
师 为什么?
生 实验1、4中,两个量不仅变化方向相同,而且存在倍数关系。实验1中,两个量是10倍的关系:505=10,10010=10,20020=10,25025=10。实验4中,两个量是6倍的关系:6010=6,12020=6,18030=6,24040=6。而实验2中,两个量虽然变化方向相同,但是没有倍数关系。
师 那么存在什么关系?
生 相差关系。
师 你们的发现很有价值!实验1、4中,两个量存在倍数关系,即比值一定,我们就说两个量成正比例关系。再深入分析一下:实验1中,两个量分别是什么?比值10又是什么?
[根据学生的回答板书:水的体积水的高度=水的底面积(一定)。]
师 那么实验4中呢?
[根据学生的回答板书:水的体积水的底面积=水的高度(一定)。]
[思考:学生找到4个实验中“两种相关联的量”及其变化规律之后,教师利用这组实验的结构化特征,汇总并加工出示数据表格,让学生对数量关系分类,使学生在比较和归纳中发现了不同和相同的数量关系,自然地建立了正比例关系的概念。]
四、在层次性练习中把握正比例的本质
师 根据正比例的定义,要判断两个量是否成正比例关系,
需要满足哪些条件?
生 两个相关联的量,比值一定。
然后,教师出示如下4个层次的练习,引导学生完成。
1.(1)一种铅笔数量和总价的对应关系如表5所示,它们成正比例关系吗?为什么?
表5 一种铅笔数量和总价的对应关系
铅笔的数量/支
1
20
30
40
……
总价/元
0.4
8
12
16
……
(2)一辆汽车行驶时间和路程的对应关系如表6所示,它们成正比例关系吗?为什么?
表6 一辆汽车行驶时间和路程的对应关系
时间/时
1
2
3
4
……
路程/千米
80
160
240
320
……
2.先把表7填写完整,再回答问题。
表7 正方形边长与周长、面积的对应关系
正方形边长/cm1234
正方形周长/cm4
正方形面积/cm21
(1)正方形的周长和边长成正比例吗?为什么?
(2)正方形的面积和边长成正比例吗?为什么?
3.每小时织布米数一定,织布总米数和时间成正比例吗?
4.回到2700年前的古埃及,和智者泰勒斯一起来测量金字塔的高度吧!
[思考:正比例关系的定义揭示了正比例概念的本质,
也是判断正比例关系的条件。本环节,教师设计了4个层次的练习。第1题是基础判断练习,呼应课始的生活情境,基于熟悉的两个数量关系,让学生判断“正确”的两个正比例关系,正向巩固概念。第2题是变式判断练习,变为数学情境,基于熟悉的正方形周长和面积公式,让学生判断“一正一误”的两个正比例关系,正反强化概念。第3题是拓展判断练习,不再给出具体的数据,让学生判断正比例关系,抽象提升概念。第4题是综合应用练习,基于数学史情境,让学生运用正比例关系解决实际问题,进一步认识正比例关系的价值。在这样丰富的层次性练习中,学生能够充分把握正比例关系的本质。]