小学数学课堂理答的几种方式
作者: 张年确
摘 要:理答既是一种教学行为,又是一种教学评价。它不仅影响着学生进一步学习的态度、思维方向,更影响着学生对问题的认知和课堂教学目标的实现。小学数学课堂中,一般有顺问利导式理答、分解纵深式理答、拓展超越式理答、纠错重建式理答这样几种方式。
关键词:小学数学;理答;提问
简单地说,理答就是学生回答问题后教师的反应和处理,是课堂问答的重要组成部分。崔允漷教授认为:“理答是一种重要的教学对话,直接影响学生对某个问题的理解和下一步的学习进程,也影响到学生对一堂课甚至一门课的学习兴趣与态度。”[1]理答与提问相辅相成,具有激励、导向、解惑等功能,能使课堂交流更有广度、宽度,促使学生更有深度、效度地思考。本文以“平面图形的面积计算”的教学为例,谈谈小学数学课堂理答的几种方式。
一、顺问利导式理答
叶圣陶先生曾言:教师当然必须“教”,而尤其致力于“导”。教学是预设和动态生成的辩证统一。教学中,学生常常会因为已有的知识和经验而产生思维定式,导致无法实现知识和经验的顺向迁移。此时,教师如能因势利导,及时调整、改变提问角度,就能使教学柳暗花明。
【片段1】 推导三角形的面积计算公式
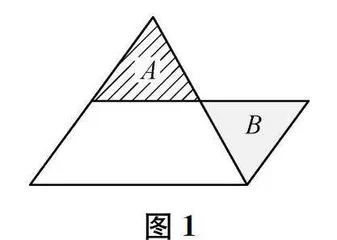
教学伊始,教师提出问题:怎样推导三角形的面积计算公式?学生的回答千篇一律:两个相同的三角形拼成平行四边形。教师继续追问:有没有其他方法求三角形的面积?学生因为思维定式使得课堂一度冷场。对此,教师改变提问的角度,进行顺向引导:请四人小组合作,用剪、拼、折等方法尝试推导三角形的面积计算公式。通过几分钟的自主探索,学生有了新的方法。一种方法如图1所示,把三角形沿中位线(当然,学生不会直接提出这一名词)剪开,把A移动到B,把三角形转化成平行四边形。受此方法的启发,学生还想到了第二种方法:如图2所示,把三角形沿中位线剪开,再把小三角形沿垂线剪开,把A移动到C,把B移动到D,拼成长方形。
教师的理答既是预设的,又是生成的。对教学中的意外、突发情况,教师要随机应变,对学生的回答作出合理的回应。本片段中,教师在课堂冷场后,提供教具让学生观察、比较、分析、概括,促使学生在实际操作中发现问题、解决问题。
二、分解纵深式理答
理答是引起、保持或促进学生课堂学习的一种重要手段。一个比较难的问题提出后,学生有可能出现没有思路的情况。此时,教师如能把原来有较大难度的问题分解为几个关联递进的小问题,引导学生通过交流讨论,逐步解决问题,便能使课堂生动、促学生发展。
【片段2】 比较平行线间两个阴影部分的大小
师 (出示图3)
你能比较图形S1和S2的大小吗?你是用什么方法比较的?
(学生表现出困惑、没有头绪的状态。)
师 要比较两个基本图形的面积,必须知道哪些条件?S1和S2之间有什么联系?你打算如何把图形S1和S2转化为基本图形?
面对学生的思维断层,教师把这样一个综合性的问题进行分解,引导学生围绕三个具体问题,通过圈画、对比、讨论、分析和归纳,轻松认识到图形S1+S3=S2+S3(如图4所示),从而把复杂的图形面积大小比较问题转化成等底等高的两个平行四边形面积大小比较问题,最终找到了解题思路。
当提问无效时,教师把概括性问题分解成几个具体的小问题,让学生通过共同商讨,自然交流,轻松对话,真心沟通,构建新的思考方式,有效促进了学生的认知发展。
三、拓展超越式理答
大教育家夸美纽斯曾说:“寻求并找出一种教学的方法,使教师因此可以少教,而学生可以多学。”因此,课堂不应是教师一味地讲解、分析和灌输,而应是教师根据学生的回答,及时铺搭台阶,提供必要的回答线索,引出与原问题相关的新问题,从而引导学生调用关联思维,实现拓展与超越。
【片段3】 计算组合图形的面积
师 (出示图5)
校园里有一个花圃,你能算出面积是多少平方米吗?
(学生交流讨论,得到图6—图8所示的三种方法。)
师 同学们很了不起,一下子就想出了三种解题思路!这三种解法有什么共同点?
生 它们都是把一个组合图形分成了两个基本图形,然后求它们的面积之和。
师 你的总结很到位!还有不一样的方法吗?
生 老师,除了用加法计算,还可以用减法计算。(展示方法,如图9所示)
先把这个图形补成一个长方形,再用这个大长方形的面积减去空白的小长方形的面积,也能计算出这个花圃的面积。
师 大家说这种思路对吗?
生 对。
师 对比这两种方法,它们有什么联系和区别?
生 相同点是都把复杂的图形转化为基本图形,不同点是第一种方法是用分割的方法转化后把基本图形的面积相加,第二种方法是用添补的方法转化后把基本图形的面积相减。
教师通过提供线索、点拨、追问,引导学生对关联性问题进行探究、交流,并得出结论,使学生受到辩证思维方法的训练,进而发展探究能力和核心素养。
四、纠错重建式理答
纠错重建式理答,是指要及时发现并指出学生的认知错误,帮助学生重建正确的认知。课堂上,学生常常会出现错误,教师如能及时纠错,把学生的思维与语言导入正轨,便能帮助学生辨清是非对错,养成自省的学习习惯。
【片段4】 计算组合图形的面积
师 你准备把组合图形分成哪些基本图形?
生 (展示方法,如图10所示)
分成一个三角形和一个梯形。
师 你能计算出来吗?动手试一试。
(学生迫不及待地动手计算,尝试一段时间后发现并不好计算。)
师 为什么不好计算?
生 不能确定三角形的底和梯形的上底。
师 对,把组合图形分成基本图形,要注意什么?
生 把组合图形分成基本图形,要考虑题目中的实际条件,不能把组合图形分复杂了。
本片段中,教师将学生的“错误”当作一种教学资源,通过强调性的反问,促使学生重新审视原来的想法,得出结论:把组合图形转化成基本图形,不仅要考虑条件,还要注意简单不复杂。这样,学生在辨析、纠正的过程中,逐渐明晰思路,强化了内省意识,提升了思维的深刻性。
参考文献:
[1]朱文君.课堂理答ABC——华东师大崔允漷教授访谈录[J].小学语文教师,2008(4):7.