感受数学的整体性

摘要：教学《分数乘整数》一课，不能只关注本节课的知识点，而要引导学生充分感受数学的整体性。具体地，可以在通过教材例题引入具体算式之后，通过算式归类，让学生在课题层次中感受整体性;通过算法探究，让学生在知识关联中感受整体性;通过算理打通，让学生在本质认识中感受整体性。

关键词：整体性;《分数乘整数》;单元教学

《义务教育数学课程标准（2011年版）》在“教学建议”中指出：“数学知识的教学，要注重知识的‘生长点’与‘延伸点’，把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系，处理好局部知识与整体知识的关系，引导学生感受数学的整体性，体会对于某些数学知识可以从不同的角度加以分析、从不同的层次进行理解。”中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012：45。

教学苏教版小学数学六年级上册《分数乘整数》一课，便不能只关注本节课的知识点，而要引导学生充分感受数学的整体性。为此，笔者的教学设计与实施如下：

一、算式归类，在课题层次中感受整体性

《分数乘整数》是《分数乘法》单元的起始课。教材设计了“做一朵绸花要用3/10米绸带。小芳做3朵这样的绸花，一共用绸带几分之几米？”的问题情境，引导学生列出“分数乘整数”的算式，探索其算法。为了让学生对《分数乘法》单元知识有一个整体的把握，笔者在学生列出算式“3/10×3”后，没有急于引导学生探究其算法，而是让学生思考：这个算式和之前学过的算式有什么不同？自然地，学生发现，这个乘法算式中有分数（之前学过的乘法算式中没有）。借机揭示单元课题《分数乘法》，并且追问：看到这个课题，你们想到了什么样的算式？这时，学生的思维被激发，提出的算式有2/5×5、2×3/7、2/5×3/4、1/8×1/4、2/5×0.5等。接着，笔者让学生将这些算式进行分类。自然地，学生将其分成分数乘整数、分数乘分数、分数乘小数等几类。对此，笔者引导学生根据小数的意义，将分数乘分数与分数乘小数合并为分数乘分数这一类。然后明确：今天我们先来研究“分数乘整数”。板书本课课题“分数乘整数”。

这里，教师引导学生在比较的基础上归类算式，在更加抽象的层面认识单元学习内容，并对单元学习内容做分类，把握单元学习内容与本课学习内容、后续学习内容的关系，初步形成单元整体知识结构。

二、算法探究，在知识关联中感受整体性

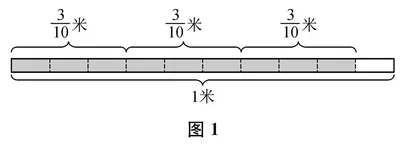
揭示相关课题后，笔者放手让学生自主探究“3/10×3”的计算方法。这一方面是因为学生已有的知识、经验足以支撑他们对分数乘整数计算方法的探究，另一方面是因为学生探究算法时不同角度和层次的思考可以充分展现数学知识之间的关联。课堂上的生成也验证了这一点。学生探究算法时，有的依据图形直观：如图1，把1米平均分成10份，每朵绸花表示其中的3份，3朵绸花表示其中的9份，即910米。有的依据单位换算：3/10米=3分米，3分米×3=9分米，9分米=9/10米。有的依据分数与小数互化：3/10×3=0.3×3=0.9=9/10。有的依据乘法的意义与同分母分数的加法法则：3/10×3=3/10+3/10+3/10=（3+3+3）/10=9/10。有的直接用分子乘整数：3/10×3=（3×3）/10=9/10。

在多种算法的展示交流中，学生充分感受到了分数乘整数与画图策略、单位换算、分数的意义、小数的意义、乘法的意义、同分母分数的加法法则等知识和方法之间的联系。在进一步的比较中，笔者引导学生发现：画图直观、单位换算、分数与小数互化、转化成加法计算这四种方法要么不具有一般性，要么比较麻烦，而直接用分子乘整数才是分数乘整数最具有一般性也最简捷的算法。然后，笔者引导学生依据乘法的意义（乘法与加法的互化）和同分母分数的加法法则，完善“直接用分子乘整数”的道理（同时明白“不用分母乘整数”的道理）：3/10×3=3/10+3/10+3/10=（3+3+3）/10=（3×3）/10=9/10。由此，让学生经历算法多样化到优化的过程，真正理解分数乘整数的算法。

此外，站在“分数乘法与分数除法”这一大单元的视角，上述算法探究活动还有十分重要的意义，是后续学习的“生长点”和“延伸点”。其一，从知识的角度看，分数乘分数的算法“分子与分子相乘，分母与分母相乘”也适用于分数乘整数，如3/10×3=3/10×3/1=（3×3）/（10×1）=9/10;分数除法的算法“除以一个数等于乘这个数的倒数”，是以分数乘法的算法为基础的。其二，从方法的角度看，画图直观、单位换算（本质上是结合具体情境的分数与整数互化）、分数与小数互化等同样是后面探究分数乘分数、分数除法计算方法的有效策略。可见，在知识的关联中感受数学的整体性，能很好地促进学生的知识理解和学习迁移。

三、算理打通，在本质认识中感受整体性

得到分数乘整数的算法后，笔者引导学生回顾比较3×3、0.3×3、310×3的计算，发现整数乘法、小数乘法、分数乘法的意义（算理的本质）是一致的，都是相同计数单位的累加（乘个数）。3×3是3个计数单位“1”乘3，得9个计数单位“1”，所以得数是9;0.3×3是3个计数单位“0.1”乘3，得9个计数单位“0.1”，所以得数是0.9;310×3是3个计数单位“110”乘3，得9个计数单位“110”，所以得数是910。由此，让学生从整体上把握所有学过的乘法计算，对“乘法计算”获得打通的一般性认识（感受到一个更大的单元整体）。

因为学习容量和学生认知的限制，教材在编排时不得不把相关的知识分散在各个不同的年段、分册和单元、课时中，但是教师在教学中不能拘泥于课时内容，而要立足知识关联以及数学整体，帮助学生有意义地理解、更系统地建构，建立灵活（纵横联系、左右逢源）、深刻（居高临下、化繁为简）的认知结构。