经历探究性过程，体验系统性学习

摘要：“解决问题的策略——从条件想起”是苏教版小学数学教材“解决问题的策略”体系中的起点知识。这部分知识的教学，既要提供任务过程具体化、知识体系模块化的学习内容，又要让学生经历探究性学习过程，体验系统性学习。《解决问题的策略——从条件想起》第一课时主要带领学生熟悉解决问题的策略，第二课时则要带领学生经历探究性过程，体验系统性学习，发展主动运用策略解决实践中复杂的实际问题的意识。

关键词：探究性;系统性;解决问题的策略;从条件想起

“解决问题的策略——从条件想起”是苏教版小学数学教材“解决问题的策略”体系中的起点知识。笔者以为，这部分知识的教学，既要提供任务过程具体化、知识体系模块化的学习内容，又要让学生经历探究性学习过程，体验系统性学习。基于教材解读和学情分析，笔者将碎片化的学习内容设计成一个网状系统，指导学生在大框架下逐步明晰细节、完善结构，通过合作探究、比较反思，形成完备的知识体系，发展主动运用策略解决实践中复杂的实际问题的意识。《解决问题的策略——从条件想起》第一课时主要带领学生熟悉解决问题的策略，第二课时则主要完成上述目标。第二课时具体教学过程与思考如下：

一、教学过程

（一）联系零散条件，初步感知数量关系

师蓝花有5朵;向日葵有8朵;绿花有12朵;玫瑰的朵数是向日葵的2倍;紫花比蓝花多4朵;红花比黄花多7朵。从这几句话中，我们能知道什么信息？

生我们能从中找到数量。

生有些还告诉了我们数量之间的关系。

师把这一个个的信息作为条件，你能从中选出两个有联系的，提出一个数学问题吗？

生向日葵有8朵，玫瑰的朵数是向日葵的2倍。玫瑰有多少朵？

生蓝花有5朵，紫花比蓝花多4朵。紫花有多少朵？

师同学们为什么不选“绿花有12朵”和“红花比黄花多7朵”这两个条件呢？

生这两个条件之间没有联系。

生因为红花的朵数和绿花没有关系，只和黄花有关。

师看来，通过有联系的两个条件才能解决一个新的问题。我们要善于从已知条件中发现问题。今天，我们继续研究运用从条件想起的策略解决实际问题。

[说明：任意给出六条信息，让学生选出两条作为条件，提出数学问题。学生会自然而然地选择有关联的信息作为条件。这样，学生再一次感受到从条件向问题推理是解决问题的一种策略，形成了新的学习需求。]

（二）自主提问探究，直观呈现数量关系

师增加一个条件——黄花的朵数是绿花的2倍。现在，这三个条件之间有联系了吗？

生有。

师根据这三个条件，你可以提出什么问题？

生黄花有多少朵？

生红花有多少朵？

师谁能完整地说说题目中的已知条件？

生绿花有12朵，红花比黄花多7朵，黄花的朵数是绿花的2倍。

师怎样才能清楚地看出三种花之间的关系呢？请先在作业纸上画一画，再在小组里说说你的想法。

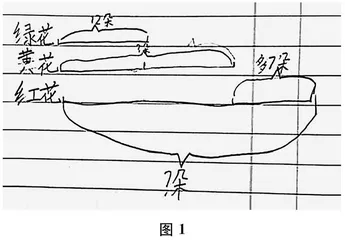
（学生活动。教师巡视，发现学生的典型画法：有的画圆代表各种颜色花的朵数，有的用直条表示各种颜色花的朵数，有的画出了如图1所示的线段图。）

师（指图1）像这样的图在数学中叫线段图。

（整合与完善学生的探究结果，出示图2，引导学生说图意。）

生根据这三个条件之间的关系，我们先画绿花，有12朵;再根据“黄花的朵数是绿花的2倍”，画出这样的两份;最后，根据“红花比黄花多7朵”，先画与黄花同样多的部分，再画多的7朵。

[说明：本环节旨在帮助学生初步学会应用线段图整理条件和问题。让学生自主探究，然后展示有代表性的学生作品，让学生在倾听同伴分享中，自主梳理、逐步抽象出线段图雏形。学生在教师的引导下带着问题思考与探究，利用直观的线段图把复杂、抽象的数量关系具体、直观地表现出来。在这样的探究过程中，学生获得了“从条件出发”和“画线段图”分析的策略，使解决问题策略的学习更加系统。]

（三）总结解题思路，形成知识结构

师刚才，我们借助线段图找对了数量关系。（板书：找对关系）根据我们找到的关系，你能列式解答吗？写下来，再说一说。提示：先根据哪两个条件求出……再根据哪两个条件求出……

[指名学生上台列式：12×2=24（朵），24+7=31（朵）。教师板书：列式解答。学生根据提示回答思路，教师根据学生的汇报完善数量关系思路图，如图3。]

师（指图3）黄花的朵数是题中的已知条件吗？

生不是。

师那又是怎么来的？

生黄花的朵数是根据“绿花有12朵”和“黄花的朵数是绿花的2倍”这两个条件求出来的，根据求出来的黄花的朵数，再根据“红花比黄花多7朵”，最终算出红花的朵数。

师是的。其实，刚才我们在解决问题的过程中，不管是画图还是列式，都是根据两个已知条件得出一个中间条件，再和第三个条件一起求出最终答案。

[说明：列式解答后，再引导学生将知识习得与方法习得做系统的梳理，将零碎的条件通过关系串成思路图。学生脑海中有了这样的网状结构，就能清晰地感受到数学知识的学习是系统的，也初步建立起有关联的“知识链”。]

（四）反思解题过程，内化解题策略

师如果把题目中“红花比黄花多7朵”这个条件改成“红花比黄花少7朵”，线段图又应该怎样改？谁来指一指，哪一段表示“红花比黄花少7朵”？要求红花有多少朵，谁能解答，你是怎样想的？

……

师下面让我们来回顾反思，（板书：回顾反思）比较这两题的解答过程，有什么相同的地方和不同的地方？想一想，再在小组里交流。

（小组交流后汇报。）

生相同点是前两个条件和问题相同，第一步都是先算黄花的朵数。

生不同点是有一个条件不同，求红花朵数的方法也不同。

师虽然两题的解题方法不完全相同，但都是从条件想起，一步步解决问题的。比较教材上例1和例2的解答过程，又有什么相同的地方呢？

生都是从两个已知的条件出发，得出一个条件，再结合另一个已知条件求出最后的答案。

生两道例题都是从条件出发去分析和解决实际问题。

[说明：反思是策略系统性学习的重要环节，策略学习中的反思可以是问题解决后成功经验的分享，也可以是探究过程中不足的“恍然醒悟”。第一次反思，学生发现：虽然两道题的计算方法不同，但相同点都是从条件想起，一步步解决实际问题。第二次反思，学生深入体会到两道题的解题策略都是从两个已知的条件出发，得到一个中间条件，再由这个中间条件和另一个已知条件求出最后的答案。通过改变条件，让学生通过两个层次的反思，进一步体验策略的形成过程，体验第一课时与第二课时连贯的系统性学习。]

（五）联系数学活动经验，系统性地运用策略

1.“策略我来说”

师最后，说说你本节课的收获。可围绕板书来说。

生我今天学到了在解决问题的过程中可以从条件想起，先找到相关联的两个条件，求出一个中间条件，再与另一个条件放在一起思考，求出最终的答案。

生我还学到了解决问题时我们要先读懂题目，找对数量关系，这样才能帮助我们正确地列出算式;解决完问题后，别忘记还需要总结反思。

生合作探究后，可以把我们的想法分享给别人;遇到不会的，可以认真倾听别人的发言，从别人的发言中我们可能会收获新的想法。

师说得真好！不光有知识层面的收获，还有学习方法的介绍，大家的收获真不小。

2.“策略合作用”

师在老师给每组装好的神秘信箱里，都有几个已知条件，你能从中找出相关联的量吗？按如下要求操作：（1）组长给每人分发一张信息条;（2）根据所给信息，在组内找到相关联的三个条件;（3）将找到的三个条件像黑板上这样贴一贴，把中间条件、所求答案填一填，完成思路图;（4）列式解答。

（学生分组交流后展示汇报。）

[说明：“策略我来说”环节，教师将发言权交给学生。学生经历了探究性的学习过程后，将学习过程与收获用精彩的语言进行了系统性的梳理。“策略合作用”环节，教师将4道课后练习题的条件打乱，让学生在已有的数学知识和活动经验基础上，选择相关条件完成思路图。整个活动设计新颖有趣，学生参与的积极性高，应用策略的意识由浅入深。这其实就是在系统性地运用策略解决实际问题。]

二、教学思考

“解决问题的策略——从条件想起”这部分内容，是在学生初步认识常见数量关系，会解答比较容易的两步计算实际问题的基础上教学的，也是解决问题策略知识体系中的关键起点。因此，这部分内容的教学至关重要。

第二课时教学，应用从条件向问题推理的思想方法，继续探索实际问题的解法。经过第一课时例1的教学，学生已经初步感受了从条件向问题的推理是解决问题的一种策略，并且初步认识了常见的数量关系。在此基础上，首先呈现几个条件，让学生找到相关联的量，提出数学问题。这样，学生不再是简单地分析条件与问题，列式解答，而是初步呈现思考的结构图，生成系统性学习的雏形。然后，增加一个条件，根据三个条件再提问题，促进学生在已有系统的框架下，加强对策略的体验。在引导学生清晰地表示出三种颜色的花之间的关系时，学生独立探究、合作完善用线段图整理题目中的条件和问题，线段图的雏形在学生脑海中自然生成。借助线段图理解题意后，教师没有让学生直接列式解答，而是给足学生探究分析数量关系的时间、空间，让学生充分交流探究过程，并逐步引导学生通过两次比较，借助数量关系思路图，系统地表达自己的思考。最后的总结环节，在体验解决问题方法的选择与使用时，学生获得了经验并建构了自己的策略，演绎了问题解决能力提升中的系统性思考与推进。

策略学习的主体是学生。本节课，从学生已有的知识经验出发，通过合作探究，使学生从经历探究性的过程走向形成解决问题的经验;引导回顾反思，使学生从杂而不精的碎片化学习转为真实高效的系统性学习。坚持让学生经历探究性过程，站在系统性学习的高度俯瞰策略，能使解决问题的策略教学成为一个整体，有机融入学生的认知结构和经验系统。