整合拓展教学内容，充分发掘教学价值

摘要：教学完小学数学中与平面图形有关的知识后，基于跨教材章节的单元整体教学理念，尝试整合拓展与三角板有关的教学内容，充分发掘三角板的教学价值，设计了《玩转三角板》一课，组织学生进行主题学习：用一副三角板画角，学会有序思考，感受基本量思想;用两个相同的三角板拼图，运用有序思考，感受基本图形作用;用四个相同的三角板拼图，培养直观想象，发挥审美创意;探索特殊图形的性质，培养空间观念，发展推理意识，感受数学文化。

关键词：三角板;主题教学;数学思想;数学文化

三角板是学生数学学习中接触较早、使用频率颇高的学具之一。苏教版小学数学教材中，有不少与三角板有关的教学内容，但是，多安排在《动手做》栏目与练习题中，比较零散。例如，二年级下册《角的初步认识》单元的一个《动手做》栏目让学生用三角板拼直角、锐角、钝角，三年级上册《长方形和正方形》单元的一道练习题让学生用三角板拼长方形和正方形，四年级上册《垂线与平行线》单元的一个《动手做》栏目让学生用三角板拼画不同度数的角，六年级上册《分数除法》单元的一道练习题让学生测量、计算三角板上30°角所对的直角边长和斜边长的比值。蒋守成.小学数学“主题创新活动”的主题确定[J].教育研究与评论（小学教育教学），2021（11）：4748。而且，这些教学内容多停留在画线、画角、测量等操作的层面，比较浅显。

因此，五年级教学完小学数学中与平面图形有关的知识后，笔者基于跨教材章节的单元整体教学理念，尝试整合拓展与三角板有关的教学内容，充分发掘三角板的教学价值，设计了《玩转三角板》一课，组织学生进行主题学习，让学生在操作活动中深度思考，感悟与三角板相关的数学知识、应用和文化以及其中蕴含的数学本质、联系和思想，提升学生的数学学习兴趣和数学探究能力。具体的教学过程及设计意图如下：

一、用一副三角板画角：学会有序思考，感受基本量思想

师（出示三角板）同学们，认识吗？能给我们介绍介绍吗？

生这两个三角板都有一个直角，都是直角三角形。

生瘦长的三角板的三个角分别是30°、60°、90°。

生还有一个三角板是等腰三角形，三个角分别是45°、45°、90°。

生三角板可以帮我们画直线、量线段的长度。

师其实，我们常用的三角板还有着更多的奥秘哦。今天，我们就一起来玩一玩三角板，看看还能玩出什么花样。（稍停）我们跳过简单的画线、量线，从角开始。如果只用一个三角板，可以画出哪些不同度数的角？

生30°、45°、60°、90°。

师如果用一副三角板，又能画出哪些不同度数的角呢？请在作业纸上画一画。

生我画出的是75°的角，我是用30°的角和45°的角拼起来的。

生我用45°的角和60°的角拼成105°的角。

生还可以用30°的角和90°的角拼成120°的角，用45°的角和90°的角拼成135°的角，用60°的角和90°的角拼成150°的角。

生还可以用90°的角和90°的角拼成180°的角。它是平角，即两条边在一条直线上。

师同学们的思考很有条理！用两个角拼着画，得到新的度数的角。在此基础上，还可以怎样画，得到新的度数的角？

生拼着画是把两个角相加，还可以让两个角相减。我先画出一个45°的角，再在这个角里面画出一个30°的角，这样就得到了一个15°的角。

生我也画出了一个15°的角，不过我是用60°的角减去45°的角的。

师（按从小到大的顺序板书：15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、180°）同学们通过努力，画出了这么多不同度数的角。如果我们带着一双智慧的眼睛去观察这些度数，或许会有新的发现。

生相邻的两个度数都相差15°。

生不对，150°和180°相差30°。

师如果这个规律存在，还差哪个角呢？你能想办法画出这个角吗？

生165°的角，可以用30°、45°、90°的角拼成165°的角。

生还可以用180°的角减去15°的角。

师照这样的规律推下去，还可以画出哪些度数的角？怎么画？

生还可以画出195°、210°、225°……的角，用不同角组合相加或相减就行了。

师这些角的度数有什么共同的特征？

生都是15的倍数。

师那么，是不是度数为15的倍数的角都可以画出来？

生是的。

师其他度数的角画得出来吗？

生画不出来。

师为什么？

生因为15是最基本的量。

师在前面画角、寻找规律的过程中，你觉得有什么重要的思考或探索方法吗？

生有序思考。

师是的。按照完成活动或构成事物的基本要素有序思考，才能不重复、不遗漏，并且更容易发现规律。（稍停）还有基本量思想。其他量都是由基本量加加减减得到的，抓住了基本量，就知道其他量的特征了。

用三角板画不同度数的角，是教材中安排的活动。教学中，笔者引导学生从一个三角板到一副三角板、从两个角相加到两个角相减再到多个角相加减、从单个角的具体度数到多个角的一般规律，不断扩展认识维度、提高认识深度，从而穷尽所有可能的角，认识它们的基本特征，同时学会有序思考，感受基本量思想。

二、用两个相同的三角板拼图：运用有序思考，感受基本图形作用

师考虑过了角，现在来考虑更加复杂的整个三角板。一个三角板是什么图形我们已经知道了，那么用两个三角板能拼出什么图形呢？

生拼成不规则的图形。

生拼成四边形。

师你们说的是两个三角板不相同（为一副）的情况。确实，两个不相同的三角板只有一组有刻度的边勉强可以重合，因此，用两个不相同的三角板拼出的图形不丰富也不漂亮。那就试着用两个相同的三角板拼拼看吧。

（学生活动。）

师用两个含30°角的三角板，有几种拼法？

生3种。

生4种。

生6种。

师到底有几种呢？谁来展示一下？

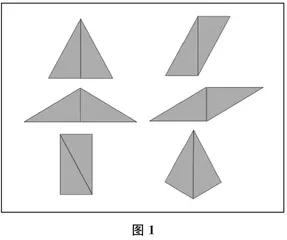
生（同步展示各种拼法，如图1所示）让较长的直角边重合，将一个三角板翻转一下，有两种拼法;让较短的直角边重合，也是两种;让斜边重合，还是两种。所以，一共有6种拼法。

师（对其他学生）有重复吗？有遗漏吗？

生没有。

师是怎么做到的呢？

生有序思考，依次考察每一组相同的边重合的一正一反两种情况。

师很好！有序思考，就可以不重不漏。那么，如果是两个含45°角的三角板，又能拼出几种不同的图形呢？

生6种。

生3种。

师究竟有几种呢？谁来展示一下？

（一位学生展示各种拼法，如图2所示。）

师同样是两个相同的三角板，为什么这次只能拼出3种不同的图形呢？

生因为含45°角的三角板两条直角边相等，没有长短区别，这样，让直角边重合时就只有2种情况，让斜边重合时就只有1种情况。

师很好！现在我们得到了9种图形，它们分别是什么样的图形？谁来说一说？

生等边三角形、一个角为60°的平行四边形、底角为30°的等腰三角形、一个角为30°的平行四边形、长方形，还有一种是……四边形。

师最后这个四边形也叫筝形，同学们以后会学到。

生等腰直角三角形、一个角为45°的平行四边形、正方形。

师这么丰富多样的图形都是由两个三角板拼成的，由此我们感受到什么的作用？

生基本图形。

师没错，基本图形在几何研究中十分重要。很多复杂的图形都可以分解为一些简单的基本图形，搞清楚这些基本图形的性质，就能搞清楚更多复杂图形的性质。

教材中让学生用两个相同的三角板拼出长方形和正方形。这里，笔者让学生系统探究，拼出所有可能的图形。学生再次运用有序思考的方法，抓住关键要素不断变化，完成了拼图。笔者的对比追问，让学生体会到认识构成事物的关键要素对有序思考的重要影响。通过对拼出的各种图形的辨认，学生初步感受到基本图形对复杂图形研究的作用，同时培养了空间观念（可以理解为“形感”），为后续深入研究图形性质打下了基础。

三、探索特殊图形的性质：培养推理意识，感受数学文化

师刚才，我们拼出了许多图形。到了初中，我们会进一步研究它们的性质。现在，我们来聚焦几个特殊的图形，看看能不能初步发现一些简单的性质。你认为哪几个图形最特殊？

生等边三角形、等腰直角三角形。

生还有长方形、正方形。

师很好！这些都是我们学过的很特殊的图形。等边三角形是由哪种三角板拼成的？由此可以发现什么性质？

生是由两个含30°角的三角板拼成的。可以发现，含30°角的三角板较短的直角边等于斜边的一半。

师非常好！虽然到了初中，我们才能证明这个结论，但是现在，我们通过观察等边三角形，就能发现这个结论。那么，等腰直角三角形呢？

生是由两个含45°角的三角板，也就是等腰直角三角形拼成的。可以发现，原来三角板的斜边变成新的三角形的直角边，原来三角板的直角边拼接成新的三角形的斜边，重合成新的三角形的高。

生所以，等腰直角三角形斜边上的高等于斜边的一半。

师很好！通过拼图，我们发现了这两个有意思的性质。到了初中，我们会进一步证明它们。（稍停）其实，这些由三角板拼成的特殊图形，正与三角板的来历有密切的关系。同学们想知道吗？下面就让我们一起来回顾这一段精彩的历史。

（教师播放视频，学生观看。画面定格于图3。）

师从视频的介绍中你知道了什么？

生古希腊时期，人们把最具有对称美的三角形和四边形，即等边三角形和正方形看成最基本的图形。当人们把这两种图形对半切开后，就得到了两种不同的直角三角形。

生古希腊伟大的哲学家、思想家柏拉图认为世界的本源就与这两种直角三角形有关，因为这两种直角三角形是最完美的三角形：沿着过直角顶点的斜边的垂线切开，可得同样形状的直角三角形。

师是啊，数学就是如此奇妙！正因为这两种直角三角形有这样的特性，人们就根据它们制成了三角板。

教材中让学生测量、计算30°角所对的直角边长和斜边长的比值。这里，笔者引导学生利用拼出的特殊（熟悉）的图形，初步探索简单的几何性质（主要是线段长的关系），在小学实验几何（主要培养空间观念）的基础上，渗透初中论证几何（主要培养推理能力）的思想，以直觉认识为基础，初步培养逻辑思维，符合《义务教育数学课程标准（2022年版）》提出的小学阶段培养推理意识，为初中阶段培养推理能力打基础的要求。然后，利用拼出的特殊（熟悉）的图形，自然引出有关三角板来历的数学史，让学生跨越时空，感受到自己的探索与古人的智慧“不谋而合”，进一步体会三角板的神奇特性以及数学审美引发的探索发现与创造，充分感受数学文化，激发学习兴趣。同时，让学生初步感受直角三角形的重要性——实际上，平行与垂直是平面对称划分的基本元素，而三角形作为最基本的平面图形，其基本性质正是平面几何（论证几何）最基础的知识。

四、用四个相同的三角板拼图：培养直观想象，发挥审美创意

师接下来请同学们发挥想象：用四个相同的三角板能拼出哪些精美的图形？