新课标视域下几何直观素养提升新路径

《义务教育数学课程标准（2022年版）》明确指出：几何直观有助于把握问题的本质，明晰思维的路径。以图助学，可以使复杂的问题简单化，抽象的问题具体化，从而达到轻松学数学的目的，提高课堂教学效率。纵览小学一至六年级共12册人教版数学义务教育教科书，新授课的例题，都附有直观形象的实物图、线段图、几何图、解题思路图等插图，教师在教学中若能依据新课标，充分考虑学生学习的自主性、探究性，引导学生另辟路径认真解读并使用好这些插图，必定能释放学生的心智和思维，激发学生学习的能动性及创造性，变新知的畏怯为探索的乐趣。

借助图解可以将抽象的数学问题具体化，有助于学生把抽象变成直观，把复杂变为简单，把数量关系清晰地呈现出来。也有助于学生更好地理解数学问题，并找到解决问题的策略。还可以帮助学生将复杂的问题简单化，使解题思路清晰化。

一、实物贴图，构建数学问题的直观模型

小学生对抽象的数学知识的理解，经常会依赖于“看”—视角能力，他们通常会把一些信息量大的数学问题想象成一组与自己生活事物为线索或背景的图像，继而应用视角模型来解决遇到的数学问题。只有用更逼近学生、更图文并茂的表达方式，学生才会更轻松理解数学概念。因此，教学中教师可以帮助学生把抽象的数学问题和直观的图形联结起来思考，把数学问题转化成图形问题，以图助学，把复杂问题简单化、具体化，引导学生在实物贴图中找到解决问题的规律。

如，在教学“植树问题”一课时，放手让学生利用学具动手合作探究，填写报告单。学生们将磁性的小树模型贴在模型小路上，在看、量、数、贴的过程中，经历“每5米栽一棵”“每5米一个间隔”“一个间隔对应一棵树”三个不同阶层的直观感知，体会了一一对应的数学思想，整个合作交流的过程都是图形与思维、算式的结合，学生在参与贴图的过程中发现了植树问题的变与不变，找到了棵树与间隔数之间的关系，明白了要求“两端都栽”的植树棵数首先要弄清路长里面有几个间隔长，也就是间隔数，若先数一个间隔对应一棵树，间隔数再加1就是所要求的棵数，“+1”加的是起点处的那一棵树，若先数一棵树对应一个间隔，间隔数再加1，这时的“+1”加的就是终点处的那棵树，凸显了“两端都栽”这一植树问题的本质，建构了植树模型。

从“栽”模型小树到“栽”充满智慧的植树模型，学生用不完全归纳法总结规律，经历知识的形成过程，学得真实又扎实，增强了学习的热情和自信心。

二、多维动图，把握数学知识的核心本质

在数学教学中，对于几何图形的学习，理解算理是至关重要的，但由于小学生的年龄特点，空间想象力还比较薄弱，只靠单纯的剪图、贴图、拼图，有些图形的计算公式的推导往往只是停留在浅层，而PPT、微课、幻灯片等多媒体辅助性教学资源在提供直观、生动、形象方面有不一样的优势，能展现难于被观察到的事物及内容，比静止的图形、模型更有动感、形象、丰富，若能着眼于教材，有效利用多媒体动图，深入解剖，学生方能学得深刻。

如，在教学“圆的面积”一课时，有了平行四边形的面积计算公式的转化策略的铺垫，学生们也会想着把圆这个曲线图形转化成直边图形。弯曲变平直，学生们往往依据直觉，把圆上弯曲的部分剪去转化成直边图形，或者把圆片进行分割重叠转化成已经学过的平面图形。在动手操作4等分、8等分、16等分的过程中，学生们通过交流讨论明白了不管怎样剪拼，形状可以变化，面积大小是不能改变的，并逐渐发现图形剪拼变化的趋势，圆等分的次数越多曲线就越接近直边。由于动手等分的局限，所拼图形的边仍有弧度，在这个关节，教师出示多媒体演示动图，动图将圆片继续往下切分，平均分的次数越来越多，学生发现图形越来越像一条线段，无限分割后，每个分割而出的图形变成一根针、一根线，此时拼出的图形就是一个长方形。经历充分感知的学生由长方形面积计算公式推导出圆的推导公式就变得水到渠成了。

显性的数学知识学生们慢慢地会淡忘，但是通过动图理解掌握重点，拓展思维深度，这个深度带来隐形的数学活动经验、数学方法思想，更容易提升学生们的核心素养，让他们终身受用。

三、实践剪图，探索解决问题的创新思路

图形是一种直观教具，能给人带来感性认知和整体感知。图形也是一种特殊语言，比通常的语言更易于让人接受。数学课上有些学生会觉得数学单调没趣味，究其原因，主要是害怕数学知识的高度抽象性，因此，如何有效帮助学生主动地参与到数学学习的过程中，数学教学图形化的作用是不可估量的。教学中教师应多鼓励学生在抽象的数学知识和直观的插图之间开创一条新路，学生们在经历动作思维到形象思维再到抽象思维的发展过程后，必定能领悟把握一些抽象难懂的数学概念。

如，在教学“24时计时法”一课时，教师可以鼓励学生把一天时针转的两圈刻度分开剪下，拉直变成两把短尺。学生在短尺上分别标出1～12，起点处的刻度线上却出现了两种情况：一部分没有标上0；另一部分标上0。在这个认知冲突处，点拨学生将短尺还原成钟表上的圆圈，从而发现钟表上不是没有刻度0，而是刻度0和12重叠在一起了。继续引导学生把两把短尺接成一把长尺用来表示一天的时间，在剪接图中，学生自然悟到长尺中间的12也是0，即钟表上第一圈结束的时间也是第二圈开始的时间，再鼓励学生关键抓住原来第二圈的刻度1和长尺的刻度13展开讨论交流得出，两把短尺是“12时尺”，一把长尺是“24时尺”，形同我们生活中使用的普通计时法和24时计时法。两种计时法上午的时刻不变，普通计时法下午的时刻加上12就是24时计时法的时刻。

像这样引导学生动手剪图直观表征时间，一方面考虑到借用学生已有的熟练的测量长度的经验，另一方面也是充分考虑到儿童视角需要直观性。学生们有了动手剪标时间尺这一直观形象的支撑，学习新知的整个过程成为学生自我沟通、自我建构的过程，获得新知的难点自然得以突破。

四、简易绘图，建立数与形的直观联系

数感是可以“算出来”，算的过程常常是学生巩固、发展数感的必经过程，这是许多一线老师在实践中达成的共识。教学实践中，发现一些数学问题中非本质的属性常常会成为学生认知的障碍，这时，教师可以创设不同形式、不同思维角度的现实载体，多鼓励学生进行观察、比较、分析，引导小学生充分利用直观的“形”，保留它们的形状、大小、位置及数量关系等方面的共同属性，及时抽象、概括，梳理清楚数学问题中数量关系，让抽象的概念内涵凸显出来，使之直观化。

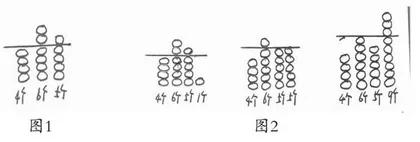
如，在教学“平均数”一课时，教师设计投篮比赛活动情境，小明连续3次投中5个球，小亮分别投了4个、6个、5个，引导学生借助××同学一分钟投篮成绩统计图（如图1），表示情境中提供的数学信息，再通过“一次比5多1，一次比5少1”启发式讲解，逐步引导学生得出“这样倒不如直接将6这边多的1给4，就都是5个”，这时，师揭示像这样通过移多补少后得到的同样多的这个数，数学上就叫作求原来这几个数的平均数。接着，师出示三幅图（如图2），让学生认真观察，独立思考，仔细计算，互相交流，说出自己的发现。

学生在直观图的辅助下，思维活跃起来了，说出了多种的想法：（1）前三次不变，最后一次变化，平均数也跟着变化。（2）平均数会随着其中的一次的变化而变化。（3）总数多4个，平均数并没有多4个，而是只多1个。（4）如果每次多4个，平均数就多4个。（5）平均数总比最大的数小，比最小的数大……其中（1）、（2）点正是平均数的“敏感易变性”，（3）、（4）点正是平均数的“齐次性”，第（5）点正是平均数的“均差之和为0”。

清晰计算的数据加上生动的直观图，辅助学生从各个不同层次，进一步达成了对平均数意义的建构，深化了学生对平均数这一概念内涵的理解与把握。

五、灵活变图，明晰思维的分析路径

当复杂抽象的数学问题中遇到直观形象的线段图，往往不需要过多的话语，学生自己就会一览了然、心领意会，这就是图形无穷的魅力。当学生的思维有了图形的支撑，思考起来也就收放自如。图形化让数学知识变得灵动起来，让学生们的眼里蹦出智慧的火花。借助图形来思考数学问题，不仅可以从图中清晰地看见题中的数量关系，还能快速找到解题路径。若学生能把一个特定的问题转变成一个个不同的图形，那就说明学生对问题已经有了自己的思路，甚至是一种新想法。

如，在教学“比的应用例2”一课时，在新知学习之前，学生已经有了分数乘除法、比的意义、比的基本性质等知识储备，教学时，不妨鼓励学生参照原图将题意用不同的图表示出来。

通过变图和说理由，学生们的解题思维活跃起来了，想出多种解法，解法一：依托图3浓缩液有一份画1格，水有四份画4格，500ml是稀释液共5份。先求每份数量：500÷（4+1）=100（ml），水的体积100×4=400（ml），浓缩液的体积100×1=100（ml）。解法二：依托图4或图5按分数乘法，也就是把稀释液500ml看作单位“1”，其中浓缩液占1/5，水占4/5。水的体积500×4/5=400（ml），浓缩液的体积500×1/5=100（ml）。解法三：依托图6用分数除法，1∶4是浓缩液和水的关系，那么浓缩液就是水的1/4，把水的体积看作单位“1”，500÷（1+1/4）=400（ml）求出单位“1”，400×1/4=100（ml）求出浓缩液。解法四：依托图4明白水是浓缩液的4倍，是倍数关系，可列出方程解，解：设浓缩液的体积是xml，水的体积是4ml。x+4x=500。也可解：设水的体积是xml，浓缩液的体积是1/4ml。x+1/4x=500。

真是一石激起千层浪，借助变图，在图中寻找新旧知识的联系与区别，寻找数量关系，从多个角度分析思考问题，诱发了学生的创新意识，激活了学生的创新思维。

总之，新课标视域下，教学中教师应该有意识地引导学生构建数学问题的直观模型，学会把数学问题图形化，启发学生从中寻找解题规律，掌握解题方法，开拓解题思路，提高多种思维能力，以期全面提升数学素养。

【注：本文系莆田市教育科学2023年度立项课题“新课标视域下小学数学大单元教学的实践研究”（课题编号：PTMS2023025）阶段性研究成果】