以问导学，在转换中理解概念

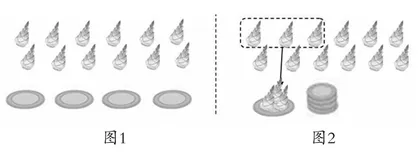
除法的初步认识是人教版数学二年级下册第13～14页的内容，是建立在“平均分”的基础上学习的，是后续学习表内除法计算及用除法解决问题的重要基础。

教材以情境呈现例4、例5两个例题。例4把12个竹笋，平均放在4个盘子里，每盘放几个？例5有20个竹笋，每4个放一盘，能放几盘？无论哪一个例题，都是解决怎样用一个“算式”表达“平均分”的过程和结果？为解决这个“问题”，重视“问题链”的设计，以问导学，在多元表征的转换中，深化除法的理解，同时发展学生思维。

一、以问导学，在转换中激活平均分的方法

教师直接呈现分竹笋的情境，并提出以下问题：

1.分的总数是多少？

2.分的标准是什么？你选择哪种方法平均分？

3.分的结果是什么？

学生观察、思考，教师请需要进一步巩固平均分概念的学生逐一交流，最后要求学生有条理完整地说一说分的过程及结果。针对图1，分的总数是12个竹笋，分的标准是平均放在4个盘子里，选择按“个”数分，分的结果是每盘分得3个，也就是把12个竹笋，平均放在4个盘子里，每盘分得3个。针对图2，分的总数是12个竹笋，分的标准是每盘放3个，选择按“份”数分，需要4个盘子，也就是有12个竹笋，每3个放一盘，需要4个盘子。

以问导学，实现了从情境表征到语言表征的转换。在转换中，强化平均分的概念，同时促进学生逻辑思维发展的过程。

二、以问导学，在转换中构建除法的理解过程

当所有学生都能清晰描述以上两种平均分竹笋的方法、过程及结果时，教师变换思维，提出怎样用一个“算式”表达平均分竹笋的方法、过程及结果？由于学生有用加法、减法、乘法算式表达的经验，为促进学生用类比的方法构建一个“新算式”的思维过程，教师提出以下问题：

1.前面已经学习了哪些算式？

2.你会选择用哪一个已经学过的算式表达平均分竹笋的方法、过程及结果？为什么？

3.这个算式是哪个？请你写出来。

4.你写的算式能表达平均分竹笋的方法、过程及结果吗？为什么？

为真实了解学生的思维过程及学生真正不能解决的问题，教师不仅要拉长独立思考的时间，而且提出学习的要求：

1.记录思考的过程及结果。

2.在思考的过程中，记录自己不能解决的问题。

好问题成就了好课堂。学生带着这四个问题独立思考，教师观察、记录学生的思考。接下来，以问导学，组织全班学生进行交流：

针对第1个问题，学生容易说出已经学习加法算式、减法算式及乘法算式。

针对第2个问题，就需要紧紧抓住“分”这个字引导学生联结新、旧知识的联系。因为减法算式表示从总数去掉一部分，得另一部分。去掉表示把总数分成两部分，这两部分可能一样多，也可能不一样多。平均分竹笋表示把总数分成几部分，每一部分同样多。它们都是在“分”，有相似性，所以选择用减法算式表达平均分竹笋的方法、过程及结果。接着，通过追问为什么不选择加法算式、乘法算式表达，进一步强化新旧知识的联结点是“分”。

针对第3个问题，顺应学生的思维，可能会写出12-3-3-3-3=0。

针对第4个问题，由于分的结果是0，而图1、图2平均分的结果分别是3和4，所以12-3-3-3-3=0只能表达平均分竹笋的过程，不能“直接”表达平均分竹笋的结果。

当学生的思维遇到障碍时，自然产生什么样的算式才能表达平均分的方法、过程及结果呢？引导学生回到起点，并让学生带着问题自学课本第13、14页及17页“你知道吗？”。

1.用哪一种新的符号表达“平均分”？

2.这个符号读作什么？你知道有关这个符号的故事吗？

3.用哪一个算式表达平均分竹笋的过程及结果？这是一个什么算式？

4.这个算式表示什么意思？

通过交流，实现了将语言表征转换为符号表征的思维过程。在转换中，知道“÷”表示平均分的意思;知道“÷”的名称，了解“÷”的由来;知道12÷4=3、12÷3=4都是除法算式;理解12表示分的总数，理解“÷4”与“÷3”表示分的标准，理解“=3”与“=4”表示分的结果，理解12÷4=3、12÷3=4表示的意思。

学生获取新知后，加强学生语言表征到符号表征的转换过程。在表达中理解数到运算关系的抽象过程，有助于学生数感的培养，有助于学生思维敏捷性、深刻性的培养。

三、以问导学，在转换中深化除法的理解

当学生建立除法这个概念时，需要学生运用新的知识解决问题，教学进入概念的巩固阶段。

1.把15条鱼平均放在5个盘子里，每个盘子里放几条？怎样列算式？根据这个算式还能编出哪些数学问题？

2.有15条鱼，每3条放一盘，可以放几盘？怎样列算式？根据这个算式还能编出哪些问题？

巩固用算式表达平均分的两种情境，实现从语言表征到符号表征的转换，从符号表征到情境表征的转换。在转换中，深化除法的理解，有助于学生思维灵活性、广阔性的培养。

以问导学认识除法，在学中强化了平均分的方法，经历用减法知识学习新知的过程，经历了发现问题、解决问题的过程，经历了独立学习获得知识的过程，理解除法的概念，促进学生思维品质的发展过程，体验学习除法的乐趣及价值，这不正是学生需要的课堂吗？