融入课程思政的导数概念教学设计

［摘           要］  以高等数学中导数的概念为例，旨在探究融入课程思政导数概念的教学设计。通过实际案例创设两个问题情境：速度问题和切线问题，归纳其共性，得到导数的概念。在讲解数学知识的同时，自然融入爱国情怀、唯物辩证主义等思政元素，从而达到价值引领、能力培养与知识传授相统一。

［关    键   词］  课程思政；导数的概念；教学设计

［中图分类号］  G712                    ［文献标志码］  A                  ［文章编号］  2096-0603（2023）08-0041-04

一、引言

2020年5月，教育部印发《高等学校课程思政建设指导纲要》（以下简称《纲要》），指出“立德树人的成效是检验高等学校教育工作是否达标的根本标准”，强调“公共基础课程在传授学生知识、培养学生能力的同时，应潜移默化地帮助学生构建正确的核心价值观，提高学生的道德素养，从而帮助学生实现自我发展”[1-2]。高等数学作为一门公共基础课程，应严格贯彻落实《纲要》对公共基础课程所提出的要求，深入挖掘思政元素，在传授专业知识的同时，自然融入课程思政，承担好其教书育人的职责。

高等数学最主要的研究内容是微积分，而导数是微积分的核心概念之一，是微积分学中解决各种问题的工具，也是学生必须要掌握的基础知识。为了让学生理解并掌握导数所蕴含的思想，而不是机械地背诵记忆导数的定义，本文从课程思政的角度对导数的概念教学环节进行设计研究。本次教学设计采用“问题教学法”“启发式教学法”等多种教学方法，结合学习通、高等数学课程思政在线课程和微信公众平台等多种教学平台，由应用案例创设情境，通过设计层层递进的问题，引出知识点，全程以问题为中心，引导学生提出问题、分析问题、解决问题，从而实现知识的掌握。

二、教学设计思路

2021年东京奥运会男子100米半决赛中，中国选手苏炳添以9秒83的成绩成功闯入决赛并打破亚洲纪录，成为电子计时时代第一位闯入奥运百米决赛的亚洲选手[3]。本节课通过苏炳添比赛过程中的速度问题创设情境：如何计算变速直线运动的瞬时速度？通过分析速度问题，引导学生得出平均速度与瞬时速度的关系，进而建立瞬时速度的数学模型。

高铁是我国创新能力的一面旗帜，也是中国名片。从中国高铁具有高稳定性的特点出发，设问：如何计算高铁运行时所经弯道的切线斜率？引导学生从生活中发现数学并一步步探索，感悟数学在实际生活中的应用之广泛。问题本身就是思政元素，既能思政，又引出了即将讲述的课程重点知识——切线斜率。通过分析斜率问题，引导学生得出割线斜率与切线斜率的关系，进而建立切线斜率的数学模型。

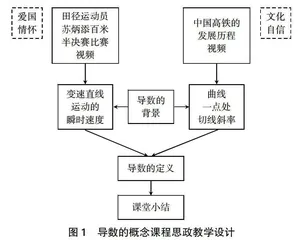
最后介绍上述两个问题的产生背景，早在十七世纪，它们就分别由数学家牛顿和莱布尼茨进行系统地研究，由这两个问题及解决相关问题而发展起来的数学理论称为微分学[4]。归纳两个引例的共性，得到本节课的重点——导数的定义。本节课的教学设计坚持育人为本，将立德树人的根本任务融入课堂教学，将思政育人贯穿始终。课前温故知新，自主预习环节，结合微积分学发展历程，引出本节课所学习的主要思想，体会数学家追求科学道路的艰辛，培养学生坚韧的意志，传承科学家的奉献精神。课中设疑启思环节，结合运动员苏炳添背景引出变速直线运动瞬时速度的计算，激发学生的学习兴趣，增强学生的爱国意识；课中深度学习环节，通过学习导数的几何意义，使学生认识数学来源于生活，也应用于生活。课后拓展环节引导学生思考导数思想在医学中的应用，通过探讨导数在医学方面的应用及相关科技前沿发展动态问题，激发学生的爱国情怀，培养学生勤于思考、勇于探索的科学精神。本节课的思政融合如图1所示。

三、教学实施

（一）教学设计

1.本节作用

导数是微积分的核心概念之一，是微积分中解决各种问题的工具，也是学生必须要掌握的基础知识。导数是一种特殊的极限，它反映了函数变化的快慢程度。导数是求函数的单调性、极值、曲线切线以及最优化问题的工具，在各个领域都有广泛的应用，是开展科学研究必不可少的工具。

学习导数的定义之前，学生已经学习了极限的定义，左、右极限的定义，极限与左、右极限存在的关系，十分利于本课开展单侧导数的学习。同时，理解导数的定义也为下一步学习微分打下良好基础，故本节课起到了承上启下的作用。

2.学情分析

本次教学授课对象为医学院校高职高专二年级学生，在以往的教学中，学生已经基本掌握了极限的相关理论：极限的定义、极限的性质、极限的计算等。通过中学时期的学习，学生已经较好地掌握了函数的平均变化率，及物理学中的平均速度、瞬时速度，积累了大量关于函数变化率的经验。二年级的学生思维较为活跃，并具有一定的归纳、概括、类比、抽象思维能力。

3.教学目标

知识目标：了解导数产生的实际背景，理解导数的定义，理解单侧导数的定义。掌握函数在一点处导数的计算方法。

能力目标：通过实例—速度—变化率的抽象过程，培养学生观察、分析、比较、归纳与类比的数学思维能力，使学生掌握从特殊到一般，由具体到抽象的思维方法。通过观察由平均变化率到瞬时变化率的“逼近”过程，体会极限的思想方法。

素质目标：微积分在漫长时期的发展历程是几代人奋斗的结果，体现了人类智慧的高度文明，反映了数学发展的辩证规律，使学生感受微积分的形成与发展，更好地把握导数的产生背景。通过介绍数学家牛顿、莱布尼茨、柯西和维尔斯特拉斯为微积分发展所作的贡献，鼓励学生克服困难，不断钻研探索。通过引入苏炳添奥运会实例，渗透爱国主义教育，激励学生的民族自豪感，增强学生的责任意识。通过导数概念中一系列的探究合作活动，使学生进一步认识合作学习的意义，增强学生的合作交流意识与能力。

4.教学重难点

教学重点：理解导数所蕴含的数学思想，掌握函数在一点处导数的计算方法。

教学难点：从具体实例到导数定义的提炼过程。

（二）课前预习

教师利用学习通发布本节课预习任务，学生登录学习通平台，接收学习资料，于课前完成任务，在线留言知识点疑难部分。

任务一：完成函数的极限，左、右极限相关测试。

任务二：自主学习，预习本课知识点并完成相应习题练习。

任务三：观看微积分学的发展历程相关视频，了解微积分学的发展历程。

（三）教学过程

1.创设情境，引入新课

引例1 变速直线运动的瞬时速度

首先播放2021年东京奥运会中国田径运动员苏炳添百米半决赛比赛视频引入新课：2021年8月1日晚，苏炳添选手在男子百米半决赛中以9秒83的个人历史最好成绩晋级决赛，创造了新的亚洲纪录，成为史上第一个跑入奥运会男子百米决赛的黄种人！展示了中国速度！赛后数据显示，苏炳添选手冲线时的瞬时速度高达42 Km/h。通过视频激发学生学习兴趣的同时，引导学生思考该视频的内涵，增强学生的“四个自信”。结合视频，提出下列三个问题。

问题一：苏炳添在比赛过程中是匀速直线运动还是变速直线运动？

问题二：如何计算苏炳添比赛过程的平均速度？

问题三：如何计算苏炳添冲线时刻的瞬时速度？

首先由学生自行解决较为简单的问题一和问题二，苏炳添比赛时跑步速度发生变化，因此苏炳添选手比赛过程是变速直线运动。根据物理学知识，平均速度等于所经过的路程÷花费时间，故苏炳添比赛过程中的平均速度为≈36.7 Km/h。关于问题三，赛后数据显示，苏炳添选手冲线时的瞬时速度达到42 Km/h。然而，瞬时速度是如何得出的呢？进而引出本次课的引例1——如何计算变速直线运动的瞬时速度。

设某质点作变速直线运动，设此质点的运动规律为s=s（t）.如何计算时刻t0的瞬时速度呢？首先，在直线上引入原点，使直线成为数轴。若t0为某一确定的时刻，则此质点从时刻t0运动到临近的时刻t0 + Δt的过程中，质点运动的位移是Δs=s（t0 + Δt）-s（t0 ），因此，根据物理学知识，在时间段t0到t0 + Δt内，质点的平均速度是运动的位移与时间的比值，即v==。若Δt越小，平均速度与这一时刻的瞬时速度就越来越接近，即随着Δt无限接近于0，平均速度v就与瞬时速度v越来越接近，即瞬时速度v就是当Δt趋于0时，平均速度的极限，v==。

通过设计由浅入深、由易到难、层层递进的问题，启发学生思考，逐步推进，不断归纳概括，得出结论：变速直线运动中，某一时刻t0的瞬时速度是当t趋于t0时平均速度的极限。

引例2 曲线任意一点处的切线斜率

首先播放近年来我国高铁飞速发展历程的视频：近年来，中国高铁飞速发展，成为我国一张靓丽的名片。中国高铁从无到有，并由“追赶者”一跃成为世界铁路的“领跑者”，见证着中国综合实力的飞跃。其中，高铁的平稳运行离不开优质的轨道设计，而设计弯道时必须考虑弯道的切线斜率，那么如何计算高铁弯道任意一点处的切线斜率呢？进而引出本次课的引例2——曲线在任意一点处的切线斜率。

中学数学将与圆只有一个交点的直线称作切线，但是这个定义不再适用于任意的曲线。因此，首先给出切线更一般的定义：设曲线y=f（x）在点P0处作与曲线相交的割线P0 Q，当Q沿着曲线趋于点P0时割线P0 Q极限位置的直线l存在且唯一，称l为曲线y=f（x）在P0处的切线。为了计算点P0处的切线斜率，取Q是曲线上附近的一动点，做割线P0 Q，则割线斜率为。动点Q沿曲线趋向于定点P0，从而割线也随之变动而趋向于切线，此时割线P0 Q的斜率趋向于切线的斜率，即切线斜率就是割线斜率的极限k=。

2.追根溯源，介绍背景

16世纪初期的欧洲，科学开始萌芽，生产力迅速发展，为满足社会需要，物理学、天文学等自然学科得到了大力发展，而这些学科与数学密不可分，因此数学也得到了大力发展。17世纪，许多科学问题亟待解决，可归结为四大类型：（1）变速直线运动的瞬时速度问题。（2）曲线的切线问题。（3）最值问题。（4）曲边图形的面积问题。上述问题促进了微积分学的产生。为了解决上述问题，许多著名的数学家、物理学家等作了大量的工作。17世纪下半叶，在前人工作的基础上，英国数学家牛顿从物理问题出发，德国数学家莱布尼茨从几何问题出发，分别给出了导数的概念。接下来介绍牛顿和莱布尼茨。牛顿从运动学问题入手，建立了“正流数术”，即微分；从确定面积的变化率出发，通过反微分计算面积，发明了“反流数术”，即积分；并通过揭示微分与积分的互逆关系论述了微积分学基本定理。莱布尼茨是卓越的语言学家，他创设的微积分符号一直沿用至今。

通过介绍导数的历史背景，让学生了解导数的发展历程，学习数学家不断创新，坚持探索的精神，并明确基础理论的重要性。

3.寻找共性，概念精讲

上述两个引例，一个来源于物理情境，一个来源于几何情境，摒弃具体意义，寻找其在数量关系上的共性，进而得到本节课的知识点——导数的概念。

设函数y=f（x）在点x0的某邻域U（x0，δ0）内有定义，x0 + Δx∈U（x0，δ0），相应的函数增量Δy=f（x0 + Δx）-f（x0），若=存在，则称函数f（x）在点x0处可导，并称此极限为f（x）在点x0的导数，记作f ′（x0）。若上述极限不存在，则称函数f（x）在点x0处不可导[5]。

4.解决问题，培养能力

经过上面的学习，学生已经掌握了导数的背景和定义，那么如何求函数在一点处的导数呢？根据导数的定义可以将求导的步骤分为三步：