大单元整合视角下小学数学运算一致性的思考与实践

摘要：小数除法教学应渗透大单元整合理念，做到以理驱法，实现运算一致性。可以分三个环节，一是基于大单元整合理念盘活教材，组成新的序列为教学的高效奠基。二是通过细致前测，依据学生真实学情而定对策。三是通过针对性较强的教学实践解决学生碎片化学习问题，促使学生举一反三，迁移应用，体会运算一致性的优势，培养学生的大单元整合意识。

关键词：小学数学；小数除法；大单元整合；运算一致性

所谓“运算一致性”，就是算理算法相互贯通。强调运算一致性，其实质是“探究知识本质、建构知识关联、感悟思想方法”[1]。部分小学生之所以视数学为“猛虎”，就是因为缺乏对数学本质的探究，缺乏“用一根线把散乱的知识串在一起”的关联意识，缺乏对数学方法的感悟、理解与掌握。这就需要教师运用大单元整合理念，通过整体构建与结构化合拢发现算理算法的联系点与一致性，演绎运算一致性的精彩。大单元整合从整体视野出发，重在体现完整教学过程的课程细胞，通过相对完整的单元总设计与学习，完成前后知识的衔接、勾连与迁移，达到举一反三或举三反一的目的。如何进行关联性开发，如何通过整体学习将“零散割裂”的算理算法贯通在一起，如何实现由碎片化学习到整体性学习的转变，无不需要大单元整合理念的深度渗透。下面仅以人教版小学数学五年级上册“小数除法”单元教学为例进行探析。

一、梳理教材寻找支点

叶圣陶“教材只是例子”的说法同样适合于数学教学。如果教师一味地“唯教材是从”“单薄”式解读教材，那么，教学的封闭、课堂教学的费时低效也就不足为怪；如果教师缺乏大单元整合意识，那么，“点”与“点”之间就容易出现“断层”，算理与算法就不容易贯通。因此，基于大单元整合理念梳理教材寻找支点不可或缺。数学学习中的支点，指向逻辑关联，指向本质勾连，指向运算一致性。

人教版小学数学五年级上册“小数除法”单元是继之前的整数除法、小数的意义和性质的学习之后而安排的，前后应该是一个循序渐进的系统过程。五个例题基本涵盖了小数除法的各种类型。其中“小数除以整数”，完全可以按照整数除法的相应规则进行计算，提醒学生注意小数点位置的处理即可。“一个数除以小数”，仍然可以迁移整数除法中的算法与算理，将“商不变的性质”进行成功迁移。“商的近似数”要求学生会用“四舍五入法”截取近似值。“循环小数”则需要学生通过有限小数与无限小数的对比理解，引入“循环节”的概念。最后的“用计算器探索规律与解决问题”，则在学生的归纳、理解与解决真实问题方面下功夫。整数除法与小数除法最关键的区别在于小数点，因而根据小数点处理方法的不同，基于大单元整合理念，我们可将五个例题整合为两个序列：除数是整数和除数是小数的小数除法。前者可以直接迁移整数除法的算理与算法，后者是前者的变式。无论是整数除法，还是小数除法，其算理是相同的，那就是：一定要平均分，计数单位分到多么细微的地步，还是要把余数的计数单位变小合并到下一个数位继续平均分。可见，“厘清小数除法的算理，是贯通整数除法和小数除法的支点”[2]。新组合后的两个序列如下（见图1）。

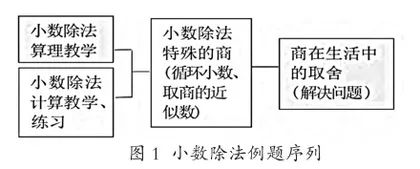
这样两个序列的实质是用算理贯穿算法，其背后的理念支撑是大单元学习。如果前期学生对整数除法中“将计数单位不断细分”这一概念掌握得不好，那么，小数除法练习中易错点的出现也就不足为怪。因此，渗透大单元整合理念，理解小数除法与整数除法的一致性，是高效学习小数除法的前提。

二、结合学情找准切入点

新的课程理念与课改强调以生为本。“本”包括所有学生的具体学情。就小数除法的学习而言，包括教材实际是否基于学生实情，是否基于学生的学习起点等。

（一）去繁存简，算式导入

悉心分析人教版教材中的“跑步的情境”，我们有一些新的思考。“跑步的情境”指向“千米与米”的单位换算，并未指向除法的算理与算法。我们舍弃这个情境，直接用两份前测问卷，对学生的学习实情进行诊断。

1.子涵用44.8元买了8个笔记本，那么，每个笔记本的价格是多少？请写出算式、过程及理由。2.算出下面算式的商并写出过程及理由：44.8÷8=（）。

随后，我们抽取五一班与五二班的学生进行前测计，发现平均正确率超过了97%，其中一个班达到了100%。这说明学生对于简单的小数除法已经掌握，实现了由抽象到形象计算的转变。既然如此，“跑步情境”所起到的作用微乎其微，完全可以舍弃，可以直接从运算的一致性进行导入。

（二）透析起点，构想策略

教师不能满足于前测一与前测二中“100%”正确率的惊喜。毕竟，能够正确计算44.8÷8的算法，并不意味着就掌握了所有小数除法的算理与算法。学生的学习起点、前知识结构、算理与算法的贯通等究竟处在一个什么样的层次上，还需进一步的前测与透析。我们用算式“16÷5”进行第三次前测，要求学生表述算理与算法。在此基础上通过细化进行等级分析（见表1）。

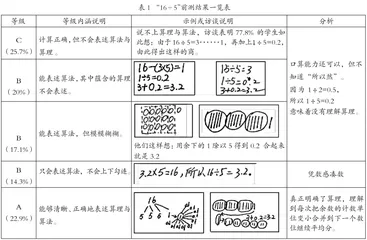
由上观之，大部分学生计算正确，但无法完整表达算理与算法。仅靠量感与口算，无法为运算一致性的掌握而助力。另外，独立完整表述算理与算法，对于五年级的学生有一定的困难。于是，基于大单元整合理念而进行整体性迁移与内化，为学生搭建支架，最终铺就运算一致性之路，就成为学习小数除法的一个基本视点。

三、教学实践过程

前测结果已经很明晰，针对实际学情采取较强针对性的措施成为关键环节。教师应基于大单元整合理念，重构教学框架，把整体性思想渗透到教学的每一个细微处。

（一）口算引入，感受认知冲突

二年级学生学习整除除法时，除不尽时用余数。现在五年级了，受其影响，不少学生还是用余数表示。既然如此，教师很有必要引领学生将余数形式转变为小数形式，实现知识上的迁移。复习二年级的知识，这已经不是“大单元”，而是“跨单元”“跨年级”。教师应实现由单薄断层到有机联系的过渡，从运算一致性上重构教学框架。

比如，口算16÷5，9÷4。根据二年级所学知识，学生得出结论：“3……1”与“2……1”。教师质疑：“五年级了，我们还要用余数表示吗？我们已经学过小数，那么，能否把这个‘1’通过小数进行细分，能否在一个更小的单位上平均分呢？”

由整数除法引入，将整数、小数融在一起，做到了上挂下联，前后关联，启发学生质疑余数“1”，进而过渡到小数除法，显得自然而然，做到了运算一致性。上述口算题看似简单，实则是整数除法到小数除法的过渡。教师应该基于大单元整合理念，引领学生由此及彼进行知识勾连、前后关联和整体把握。

（二）多元表征，体会算理理解

如何巧妙处理余数“1”，仍然需要大单元整合理念。1÷5究竟是0.2还是0.02，需要贯通整数除法以及小数除法的算理。我们的做法是通过多元表征，融会贯通，让学生体会算理，体会运算一致性，做到知识的迁移与应用。

学生用竖式计算出商后，教师及时发问：请大家观察竖式，与过去学习的整数除法比较一下有什么不同？是不是余数变大了？由“1”变为“10”了？因为有了小数点的加入，这个“10”所代表的意义就不一样了？你是如何理解的？请把自己的想法画出来（见图2）。

经过仔细观察，教师与其他同学理解这个同学的想法：10个0.1除以5，结果是2个0.1，如此，哪里应该点上小数点，2应该写在什么位置上，2个0.1意味着什么，自然就一目了然了。

可以发现，上述过程隐含着可迁移的思路：将小数问题转化为整数问题进行思考与解决，即将未知转化为已知。而这，正是运算一致性的具体体现。其中的前提是：小数除法与整数除法的算理是一样的，都离不开除法“平均分（不断细分）”这样的本质。尤其值得提倡的是引领学生“画出自己的想法”这一环节，彰显着我们对学生的信任———师生能够从学生喜欢的方式中发现问题，分析问题，解决问题。这给我们一个提醒：鼓励学生经常性地进行多元表征，必能让学生的思维好好伸展。

（三）迁移推理，感受运算本质

学生理解了把几个一转化成几十个十分之一，那么，碰到更多“数要细分”并且“平均”分时怎么办？能否举一反三，掌握能够贯通所有小数除法的普遍的算理呢？于是，进一步迁移推理就成为巩固小数除法学习中的应然。

引领学生认真观察竖式（见图3），针对其中的“10”与“20”，教师提出质疑：“这里的10与20表示什么呢？”显然，学生能够很快得出结论：“是因为0.1不够分了，所以要变成新的计数单位继续分。”所谓“变成新的计数单位”就是再次添0。以此类推，0.01、0.001等的出现就是必然的，直到解决问题。教师趁机进行结构性合拢：“整数除法的本质是什么？不就是计数单位不断细分的过程吗？整数除法与小数除法两者的本质是一样的，只不过小数除法增加了小数点的位置与如何添0的问题。”

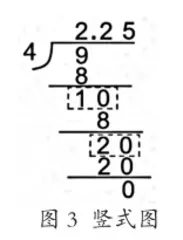
这样的迁移推理基于本单元而超越于本单元，体现出整数、小数除法运算的一致性，算理、算法融为一体，并且做到了以理驱法，完成碎片化学习到结构化学习的过渡。针对那些对整数除法掌握不扎实，同时小数除法练习中经常点错小数点、漏0或者多0的学困生，这样的迁移推理尤为重要。教师应该多多关注学困点，引领学生在有意义的迁移中体会运算一致性的作用，一点一滴地提升其数学学习力。

（四）对比梳理，凸显算理一致

利用“商不变的性质”，学生在小数除法与整数除法中很容易地进行转换。既然“被除数和除数同时除以相同的数（0除外）后商不变”，那么，碰到稍难或者不能立即“看出眉目”的题型，学生完全可以通用这一性质，将未知问题转化为已知问题（将小数除法转为整数除法问题）进行对比梳理。而这，同样离不开大单元整合意识。

1.计算并观察1.6÷0.5和16÷5的商，学生积累了一个经验：除数是小数的除法，利用“商不变的性质”转化为整数除法的形式，可以轻松解决。

2.搜集并展示部分学生完成的几组算式（包括错题），引领所有学生对比观察，从中发现算理及算法，进一步理解“商不变的性质”（见图4）。

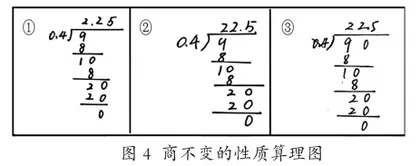
三个对比算式的梳理中，从9÷0.4到90÷4，就是运用了商不变的性质。显然，上述过程中从9÷0.4到90÷0.4就与“商不变的性质”形成矛盾。学生不难发现，后者没有做到“同时”二字。由此，学生进一步理解了除法的基本性质，理解了运算一致性的优势。对比梳理中，不同章节的知识点在一个更整体的角度上得到了整合，知识树渐渐形成，大单元整合的意义得到了充分的体现。

可见，引领学生始终以理驱法，体会运算一致性，能够“促使学生形成科学严谨的思维习惯，培养推理意识”，更重要的是培养学生的迁移意识、单元整合意识及整体思想[3]。在一个更大的视野中将知识要素进行整合，发现其内在机理与普遍规律，实现运算一致性，学生视数学如“猛虎”的现象将不复存在。

参考文献：

[1] 王玉彬，姚颖.探索运算本质构建运算联系[J].小学数学教育，2022（5）.

[2] 侯燕妍.以理驱法，体会运算一致性[J].教学月刊（小学版），2023（1-2）.

[3] 冯玉新.注重“一致”整体施教贯通“理法”促进学习[J]. 福建教育，2023（1）.

编辑/赵卓然