真实情境：数学默会知识显性化的重要路径

摘要：默会知识的本质是一种判断力、领悟力和理解力，默会知识的学习是发展学生数学核心素养的应然追求。纵观当下小学数学课堂教学，默会知识的教学仍存在“三重三轻”的问题。默会知识的情境性告诉我们，默会知识的习得往往都贯穿于情境之中。真实情境能帮助学生更好地学习默会知识，让默会知识发声，从而发展学生的数学核心素养。

关键词：小学数学；真实情境；默会知识；显性知识

在学习的过程中，遇到了这样一道习题：一张长是18.84厘米，宽是12.56厘米左右的长方形纸卷成一个空心圆柱，体积最大是多少？

不难发现有两种卷法，一种是以长作为底面周长，另一种是宽作为底面周长（见图1）。通过计算发现，以长作为底面周长，得到的圆柱体积会更大。出乎意料的是，很多学生只计算了一种情况，就是以长作为底面周长计算。

当笔者进一步追问学生是否考虑到以宽作为底面周长时，很多学生否定了我的猜想，只是主观经验上认为长作为底面周长得到的圆柱体积会大一些。也有学生认为不管怎样卷，体积都一样大，所以只需计算一种情况。作为教师知道，把长作为底面周长的时候体积会更大，这背后有着精准的推导证明。

学生的这种主观经验引起了笔者深思，这种凭主观经验来解决实际问题是个例吗？

经过调查，笔者发现很多教师遇到过同样的现象。在数学学习的过程中，凭主观经验做出了选择和判断，缺少对真实情境的深度思考，有时候做出的判断和选择是正确的，而有时候，这种主观经验又起了“副作用”。

一、诠释：学科核心素养下默会知识的意蕴

（一）默会知识的起源

这一现象其实早就引起了许多学者的关注。20世纪60年代，英国思想家波兰尼就提出了“默会知识”（tacit. knowledge）理论（也称“缄默知识”）。默会知识指人类知识中无法言语表达或是表达不清楚的知识。波兰尼强调，“我们所知道的远大于我们所能表达的。”与之对应的是“显性知识”，显性知识是指通常意义上可以用概念、命题、公式、图形等加以表述的知识。

（二）默会知识的特征

默会知识有很多鲜明的特征：第一是情境性，默会知识因为无法靠一般语言传递，所以让学生在情境中去体会和领悟就显得特别重要了，特别是感“悟”学习的过程。正是因为默会知识的情境性，才有真实情境中，把默会知识转化为显性知识的可能。

第二是个体性，不同人的成长环境不一样，就算是同一个班级的学生，教师一样，上课内容一样，但是家庭环境不一样，社会环境有区别，先天上的差异等原因，这种差异在默会知识的表现上会更加明显。

第三是层次性，默会知识按照能够意识表达的层次被分为三个层次，一是能够被意识到，并且能被表达的知识；二是能够被意识到，但是表达不清楚的知识；三是无意识的知识[1]。默会知识的层次性，为默会知识转化为显性知识提供了可能。

二、溯源：数学教学中默会知识的梳理

随着研究的深入，笔者发现当下的数学课堂中，虽然有一些教师已经关注到了默会知识，但是关于默会知识的教学仍存在很多不足。

（一）重经历，轻领悟提升

在文章开头的练习中，很多教师都会引导学生计算比较两种情况。站在教师的角度上来看，学生在经历了分类、运算、比较和得出结论的过程，会对以上知识点印象深刻从而掌握知识，并且进一步理解只要是长方形纸卷成空心圆柱，一定是以长作为底边所得到的圆柱体积比较大。

这样的教学注重了学生的计算经历，但是缺少了学生的领悟过程，学生并不是自己主动去计算比较的，是因为教师的引导提出，才有了进一步的思考。而当学生自己遇到新的问题时，又会不知所措。教学过程中，教师没有停下来，让学生去想一想，这样两种不同的卷法，光凭想象可以比较出体积的大小吗？如果看不出来，又该怎么办？最后回归到推理运算。从默会知识的角度来说，教师只注重了推导过程这一显性知识，而忽视了这道题目背后的默会知识。这就导致很多学生对于默会知识的掌握程度不同，这也是为什么有的题目教师讲解之后，有的学生掌握了一类题，而有的学生只掌握了一道题的原因。

（二）重判断，轻逻辑推理

在上述教学过程中，教师在最后会强调“只要是长方形纸卷成空心圆柱，一定是以长方形长为底边周长卷成的圆柱体积比较大”这一结论。

教师在实际教学中，遇到学生反复讲解还不会时，就会让学生“记结论”。这样的做法看似是给学生积累了数学学习的基本经验，实际上忽视了重要的数学思维。对于较为复杂的知识点，如果只是停留在识记上，会导致很多时候学生做出错误的判断，得出错误结论。“差之毫厘，谬以千里”，数学是一门严谨的学科，只要对题意稍作改动，可能意思就发生了根本性改变。比如“圆的直径是半径的两倍”这个结论的成立，必须是在同一个圆或是相同大小的两个圆这个前提下。

在教学以上显性知识的同时，忽视了背后的默会知识，即对推理能力缺少进一步的认识，忽视了培养学生优质的思维品质。

（三）重回顾，轻反思提炼

著名数学家、数学教育家弗赖登塔尔曾说过：“只要儿童没有对自己的活动进行反思，他就达不到高一级的层次。”这里的“高一级的层次”不仅包含思维上高一级的层次，从默会知识的角度来看，反思可以帮助学生把默会知识显性化，在显性化的过程中，提高学生的思维水品，达到思维的进阶。但是现实情况是课堂的反思经常流于形式，使得默会知识显性化这一过程被忽视。

在一开始的教学中，很多教师在教学完整个知识点之后，是不会对于这道题目进行反思提炼的，学生只会知道这道题目的结论，而不知道解决这类探究性题目需要哪些程序性知识。比如我们一般需要经历猜想———验证———归纳———总结等过程，并且在得出正确结论之前，这样的探究过程可能是会反复经历的。教师的忽视导致这种默会知识的习得往往都是学生自发的，而基础薄弱的学生不会这样去反思提炼，这就导致优秀的学生习得的默会知识远多于基础薄弱的学生，优秀的会更优秀，这也是班级学生出现“两极分化”的重要原因。

三、建构：教学的真实情境下，默会知识的外显

真实情境是指源于现实世界、贴近学生经验的生活场景，具有复杂性和开放性[2]。真实情境有丰富的信息，基于学生的生活经历，以培养学生“四能”，发展学生核心素养为目标，引导学生积极主动地融入数学学习，更好地理解数学知识之间的联系，提升数学学习的领悟力，理解力和判断力。

《普通高中数学课程标准（2017年版2020年修订》把教学情境分成现实情境，数学情境和科学情境[3]。《义务教育数学课程标准（2022年版）》（以下简称新课标）中提出，真实情境创设可以从社会生活、科学和学生已有数学经验等方面入手[4]。纵观课程标准可以发现，课标对于情境的分类是相同的，高中数学课标中默认了情境的真实性。

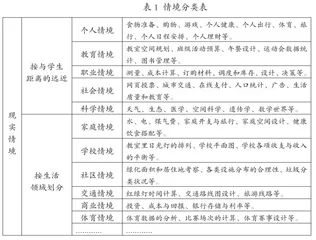
PISA按照情境与学生距离的远近将情境分为个人情境、教育/职业情境、社会情境与科学情境。或者根据生活的不同领域对情境进行划分，挖掘出家庭、学校、社区、交通、商业等多个领域的情境（见表1）。

观察上表能够发现，PISA的现实情境和课标中的定义不同。这个“现实情境”和我们所说的“真实情境”更为接近。虽然名称上有所不同，但是根据PISA的分类，的确为我们的课堂教学提供了很多可以参考选择的“真实情境”。

（一）在真实情境中感悟默会知识显性化的需要

在《和与积的奇偶性》中，很多教师开门见山，用几个加法算式直接去探究和的奇偶性。但这样的导入略显生硬，引不起学生的学习兴趣，最重要的是由于学生学得不主动，导致很多学生忽略了和与积的奇偶性背后的默会知识。一方面，学生和教师只注意了本节课的显性知识，即和与积的奇偶性，忽视了探究过程中学生主动获得知识的过程，即“猜想———验证———归纳———概括———总结”这一系列解决探究性问题的一般过程。这才是本节课的重点。另一方面，以上的显性知识真的是被所有学生掌握了吗？有教学经验的教师不难发现，有不少学生对于以上显性知识掌握得不牢固，一到运用就会出错，这说明有不少学生的学习停留在浅表层，也就是在简单重复。所以本节课的情境引入主要解决以上两个问题。

情境：小文和小雅去图书馆借书，发现一本图书的某一页破损严重，他们想要把这一页修复好。两人在修复过程中遇到了争执，小文说：“我记得这一页正反页码之和是34。”小雅说：“我记得这一页正反页码之和是33。”你觉得谁记错了呢？为什么？

以上情境的引入，让学生产生了探究一本书正反页码之和的内驱力，在探究说理的过程中，我们能发现一本书某一页正反页码之和都是奇数，这就引出了今天所要学习的和的奇偶性的知识。探究说理的过程，其实就是默会知识显性化的过程。在这样的探究过程中，学生是积极思考，自主探索，最后是合作交流的。在整节课中，学生不仅知道了“奇数+偶数=奇数”这样的一个显性知识，更重要的是经历了探究过程，掌握解决这一类问题的一般方法，体会用数学的眼光观察世界，用数学的思维思考世界，有利于学生思维走向深处，促进数学核心素养的落地。

（二）在真实情境中学习默会知识

1.在现实情境中培养领悟力

在当下的教学中，学生分析和解决的问题往往是单一的、条件完备和结构封闭的问题。和现实生活中所遇到的真实的、复杂的情境是绝不一样的，显而易见的是，真实情境中的问题会更难解决。

在《认识平均数》这一课中，苏教版数学书中创设的是男、女生套圈的情境，由于人数的不同，我们要比较男女生哪一组套得准时，只能选用平均数，这样的引出的确更加合理。这在帮助学生学习平均数的计算方法和意义时，显得游刃有余。

但是如果更进一步去思考，这样的学习真的落实了学生的数据意识和应用意识吗？

教师不妨从默会知识的角度去思考，本节课的显性知识就是平均数的意义和方法，默会知识是为什么可以用平均数来表示这组数据，培养学生的数据意识和应用意识。为了更好地落实默会知识的学习，教师可以创设更贴近学生生活的情境。

情境：校门口一到早上上学和傍晚放学就堵车堵得厉害，为解决校门口堵车问题，你打算怎么办？

在这个情境中，数据都没有告诉学生，这样一个开放的、劣构的问题，往往需要学生付出更多的思考。要解决以上问题，我们必须把这个复杂的问题分解成多个单一的问题。

一是要知道上下学时学校周围的车流量，而一天的车流量显然不能代表所有的时间，所以学生又必须多去统计几次上下学的时间内的车流量。二是这里涉及到统计的方法，比如前面学习的画正字等，还要用到统计表，学生要选用合适方法。三是引出平均数的概念，也就理解了平均数表示一组数据的整体情况。最后更为重要的是，我们还要给出相应的解决这个现实问题的策略，比如，我们可以采用分段上下学的办法，以缓解某一时间段内车流量过大的现象，实行一段时间之后，可以再统计一段时间的车流量，看看上下学的堵车现象有没有缓解。

在这样的学习过程中，学生不仅学到了平均数的算法和意义这一显性知识，更重要的是，学生在潜移默化中理解了为什么要求平均数，并且领悟到平均数是为我们解决问题所服务的，在解决这个问题的过程中，发展了学生分析问题和解决问题的能力，培养了学生的数据意识和应用意识，让核心素养的培养贯穿于整节课。

2.在数学情境中培养理解力

在平时的教学中，很多教师只注重显性知识的学习，而忽视了学生的理解，对于背后的默会知识采用“随缘”的态度。针对以上现状，我们设置了以下的数学情境，帮助学生提高发现问题和提出问题的能力，并且在解决问题的过程中，让学科知识融会贯通，理解数学学习的一般方法，知识的获得不仅是要求全，更要求联。