A* 解锁校园之旅：路径规划与智能决策

项目简介

学生初到校园，不熟悉环境，常常找不到合适的路径快速到达想去的专业教室。基于这一真实情境，本项目尝试解决的核心问题为：如何利用人工智能技术解决校园找路困难的问题？

项目规划

本项目中，学生将综合运用信息技术、数学和地理学科的知识与技能，学习如何将复杂的校园平面地图进行抽象表示，巧妙运用搜索算法进行精准的路径规划，并通过回归分析技术，实现智能化的决策过程，最终优化路径选择，培养跨学科学习思维和问题解决能力。

项目目标

本项目旨在让学生通过校园路径规划的项目学习，能够知道地图的抽象表示、搜索、回归等基本概念，对智能决策和搜索算法有所了解，进而理解将路径规划技术应用于解决生活中问题的基本思想和方法。

项目实施

项目依据问题解决的基本过程设计了4课时，单一课时重点解决1个小问题。每个课时的设计思路都遵循从现实世界形成问题，提炼对应的计算机问题，利用学科知识学习、理解计算机对这类问题的解决方案，再将其应用于实际问题的解决，甚至推广到生活中更多问题的解决。

建立数据基础：抽象地图

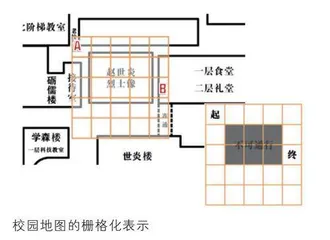
用5×5的栅格地图对学校地图进行栅格化表示机器人眼中的地图表示形式有很多，比如点云地图、栅格地图、拓扑地图、语义地图等。其中，栅格地图是用一个个方格组成的网格代表地图，栅格里可以存储不同的数值，代表不同的含义。本阶段，学生需要将真实的平面地图进行栅格表示，并用0或1标记栅格的可通行状态，为在程序中表示校园地图作准备。

利用二维数组表示栅格地图每个点的位置

无论是Python、C++还是MATLAB，矩阵更适合数组的表达，更便于编程。在这一活动中，学生能够利用二维数组表示地图中的点位，比如设定起点为[1，3]，终点为[7，7]，并尝试找到可通行的路径，为路径规划作铺垫，也为后续问题的解决奠定基础。

A*算法助力：启发式搜索

热身活动

提出现实问题，比如从教室到食堂的路线有哪些？哪条最短？让学生想一想、画一画，激活学生的思维。然后，引出路径规划的概念及其在生活中的应用，比如手机地图导航中的路径规划、扫地机器人的清扫路线规划、商场中快速查找商铺的路线规划等，进而引出本课的重点内容——搜索算法。

让计算机找到最短通行路径

学生合作学习模拟计算机寻找最短路径的方法，并归纳提炼出盲目式搜索的典型方法，即深度优先搜索和广度优先搜索。学生在讨论过程中指出：盲目式搜索效率比较低，如何才能更智能一些呢？

更加智能地找到最短路径

通过更多的提示信息，可以“启发”计算机更加智能地搜索，学生依托多样学习资源的帮助，逐步理解A*算法的关键：如何寻找最优节点？启发函数如何估算距离？A*算法为了寻找到最优的下一步（最优节点），需要估计经过候选节点的从起点到终点的路径总长度（F），即从起点到该节点的实际路径（G）加上从该节点到终点的最短路径（H）。而最短路径（H）需要通过启发函数进行估算，这里的启发函数使用的是欧式距离（两点之间线段最短）。

应用A*算法解决实际问题

学生明确了A*算法的原理后，就可以模拟计算机的运算过程，最后通过运行程序代码验证问题解决。此外，通过对比和评价本课涉及的3种算法效率，加深对于搜索算法思想的理解。

解决方案优化：回归分析与智能决策

随着对知识原理的深入学习，学生发现了更多细节问题。比如，他们意识到由于学校内不同区域在不同时间段的人流量存在差异，因此仅仅依赖启发式搜索得出的最短路径，在实际应用中可能并非总是最优选择。面对这一问题，他们继续进行深入思考，探究课间休息时长与人流量的关系是否会对路径规划的结果产生影响。

课前数据准备

首先，要进行数据收集与处理，学生结合数学统计的知识和方法，建立起不同课间人流量的数据基础。学生记录了不同课间时段学森楼前一段路径的通行人数，包括普通课间、课间操课间、午休时间、眼保健操课间等。

线性回归模型建立

课上，学生通过“探究小车的运动速度随时间变化的规律”这一物理实验的引例，体验了线性回归预测方法及过程。然后，学生需要学习利用Python中的sklearn及matplotlib模块，实现线性回归算法并解决实际问题。根据学生统计的课间休息时长与人流量的数据，编程求得人流量与课间时长之间的定量关系。借助Python编程语言中的sklearn模块探索两个变量之间的线性关系，并以时长为x轴，人流量为y轴，通过matplotlib模块绘制出拟合图像。

最小二乘法优化

对照机器学习的一般过程解析程序代码，学生可以明确和理解运用fit、predict及score训练数据，得出模型、使用模型预测结果的方法。LinearRegression最小二乘线性回归的优化技术是将残差平方值和最小化作为目标，从而使预测数据与实际数据的误差平方和最小。

综合考量：智能决策

经过程序运行，得到的人流量与课间时长之间的关系式为：y=12.54x-89.2；R2为0.94。算法训练完成后，得到的R2比较接近1，说明训练得出的模型效果较好。由此可见，给定一组数据，在假设数据间存在一元线性关系的前提下，就可通过机器学习中的线性回归算法拟合数据。

项目评价

项目学习效果评价包含多个内容和多种评价方式。进行过程性评价时，综合考量了学生的课堂参与程度、每课时项目学习单的完成质量，以及学生的自主评价，全面评估学生对于核心知识的掌握情况及项目实践的进展。进行总结性评价时，依托项目报告的完成情况，包括利用北斗系统测绘校园平面地图、实现学校地图的抽象建模、借助搜索算法和智能决策得出的路径规划结论等，考查学生对于项目主要知识的整体掌握程度，以及在问题解决过程中核心素养的体现与提升。