捕捉生长契机 落实核心素养
作者: 石雨卓
[摘要]文章以“数轴上的动点问题”为例,在分析问题时,抓住学生的生长契机,引导学生多角度思考并采用分类讨论的方法解决问题,培养学生数形结合的思想,落实对学生抽象能力和模型观念等核心素养的培养.
[关键词]生长契机;数学素养;动点问题
背景分析,思辨之始
“数轴上的动点问题”横跨代数和几何两大数学领域,融合了方程模型和数形结合的思想.这类问题要求学生从动态的视角和联系的观点出发,分析、掌握动点的运动规律.动点问题的抽象性与多变性容易使部分学生在解题时望而生畏,于是这类问题便成为他们学习路上的拦路虎,导致方程模型、抽象能力等数学素养以及分类讨论和数形结合的数学思想难以形成[1].
设计施教,思想之旅
(一) 设计框架
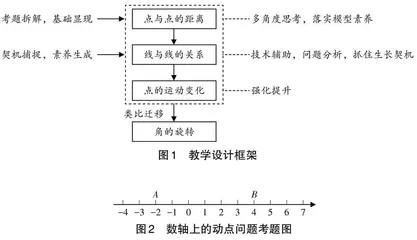
笔者以诸暨市2024学年上学期数学期末考试的一道考题为切入点,进行变式教学,通过引导学生进行分类讨论、多角度思辨以及类比迁移,落实对其抽象能力和模型观念的培养.教学设计框架如图1所示.
(二) 教学实施
1. 考题拆解,基础显现
预习任务:
如图2,点A,B在数轴上表示的数分别为-2与4,若数轴上A,B两点之间存在点C,使得AC=2BC.
(1) 点C所表示的数为______ .
(2) 动点Q从点B出发,以每秒1 个单位长度的速度向右运动,假设运动时间为t 秒,求:①当t 为何值时,QC = 3.
设计意图 通过增加基础题型,对考题进行拆解,引导学生从线段和点这两个不同的角度用代数式刻画研究对象,既列出方程解决问题,又复习回顾知识点,起到“以题知理”的效果,同时为后续分类讨论奠定基础.
学生反馈 不难求得点C 所表示的数为2.对于第(2) 题第①问,学生均能列出方程,且有两种解法.
生1 (线段和差角度) 根据动点Q的运动状态可知QB=t,则QC=QB+ BC=t + 2.所以根据QC =3,可列方程t +2=3,解得t = 1.
生2 (两点间距离角度) 根据点Q的运动状态可知,当运动时间为t 秒时,点Q 表示的数为4 + t,不难发现点Q永远都在点C 的右侧,所以可得QC =(4 + t)-2 = t + 2,同样可列方程t +2=3,解得t = 1.
教学反思 虽然两种解法均有学生作答,但基础较差的学生未想到用方程模型解题.因此,可对预习题目进行改进,专门为基础较差的学生增加特别提示:用包含时间t 的代数式表示QC的长度和点Q的位置关系.
2. 契机捕捉,素养生成
如图3,在预习题中增加动点P:从点A出发,以每秒3个单位长度的速度向右运动.求:②当t 为何值时,PC = 3;
③当QC =2PC 时,求t 的值.
设计意图 通过变式,逐步完善,直至期末考题呈现.在课堂中采用动画演示,引导学生分析题意,从中抓住生长契机,引导学生分类讨论.
学生反馈 对于第②问,可从动画中直接观察到点P 随着时间发生变化,并且可从两点间距离的角度进行刻画,具体反馈如下:
生 根据点P的运动状态可知,当运动时间为t 秒时,点P表示的数为-2+3t. 而PC有两种情况:点C的坐标减去点P的坐标和点P 的坐标减去点C 的坐标.
此时,教师应抓住生长契机追问:为何有两种情况?
生 有时候点P在点C的左边,有时候点P在点C的右边.
师 有时候…… 有时候…… ,能否用代数式明确有时候是什么时候?并求出t 的值.
实践表明,从两点间距离的角度解答,思路较为烦琐;若改用线段和差的角度,从绘图中直接分析也可得到PC 长度的表达式. 此时,抓住两个角度作比较这一生长契机,引导学生辨析两个角度的区别,如表1.
教学反思 通过变式,抓住学生对两个角度解答的难易程度不同这一感受的契机,引导学生结合研究对象和所需要素辨析两者的适用情况,达到“以题知理”的目的.
变式2 动点P从点A出发,以每秒3个单位长度的速度向右运动,当点P与点Q相遇时立即改变方向,向左运动,速度不变;同时,动点Q从点B出发,以每秒1个单位长度的速度向右运动,假设运动时间为t秒,求当t 为何值时,QC=2PC.
设计意图 通过对原题进行再次变式,增加临界点的分类讨论.同时,利用信息技术进行演示,引导学生画图并分析相应情况,强化正在形成的分类讨论思想.
教学反思 通过例题和变式1的动态演示辅助解题,大多数学生都能在变式2中自主地进行分类讨论并作图分析.因此,可以在学生解答完题目并点评之后,展示变式2的演示,以此进行验证并增强学生的成就感.变式3 动点P 从点A 出发,以
每秒3个单位长度的速度向右运动,同时,动点Q从点B出发,以每秒1个单位长度的速度向右运动,假设运动时间为t秒,求:
①当t 为何值时,点C 为PQ 的中点;
②当t 为何值时,C,P,Q中任意一点是其他两点的中点.
设计意图 通过对所求条件进行变式,发现此时用点的位置来解答较为简便.引导学生辨析应当根据所求的对象来选取解答角度,从而完成“角度选取”这一自然生长.
教学反思 所求条件变动过大,导致基础较差的学生未能联想到中点公式.因此,可以在第①问前增加问题,降低难度,例如:当t = 2时,点C为PQ的中点,求点C表示的数.
3. 学习类比,迁移应用
如图8-1,已知点O 在直线AB上,射线OD,OC 分别在直线AB 的上、下两侧且∠COD = 80°,OE 始终是∠AOD的平分线.
(1) 若∠AOE = 10°, 求∠COE的度数;
(2) 如图8-2,设∠AOD = n°,已知∠DOE =2∠AOC,求n 的值;
(3) 如图8-3,在满足(2)的条件下,射线OP从OB出发绕点O以每秒4°的速度逆时针旋转,射线OQ 从OE出发绕点O 以每秒2°的速度顺时针旋转,射线OP,OQ同时开始旋转,记旋转时间为t 秒(0 ≤t≤45) . 当∠QOD和∠EOP互余时,求旋转时间t 的值.
设计意图 从数轴上的动点,到角的动射线,引发学生进行“类比学习”的自然生长,强化分类讨论、数形结合的思想,以及方程的模型观念.
教学反思 此题作为课后练习,已有绝大部分学生进行了分类讨论、作图分析并列方程解决问题.由此可见,学生已逐步学会透过题目认识数学本质,从而自然发展数学素养.
沉淀启示,思索之灯
(一) 语言之芽,契机之土
在教学过程中,教师需时时处处留意学生的日常用语,寻找那些根植于日常生活的教学契机,从而有效地引导学生进行分类讨论和数形结合的深入思考.这不仅促进了学生的自然成长,还巧妙地种下了数学素养的种子,让它们在学生的脑海里生根发芽、茁壮成长.
(二) 科技助航,理解之桥
面对抽象难懂的数学难题,信息技术的运用犹如架设在理解河流之上的桥梁,能使学生轻松跨越理解的鸿沟.通过动态演示,学生能够在自主描绘的过程中,逐步深入到问题的核心,从而在深刻理解的基础上解析问题.因此,除了在课堂内应用信息技术,课后教师还应尽可能地安排一系列同类题目的练习,以此巩固和深化学生通过技术获得的理解,让技术在学生的心中留下深刻的印记.
(三) 多角探索,思维之翼
在教学过程中,引导学生从多个角度审视和思考问题,是拓展其思维和视野的关键.教师应鼓励学生多角度地对问题进行探索和思考,这样的教学策略,不仅能够增强学生的问题分析和解决能力,而且能够为他们的思维插上翱翔的翅膀,让他们在数学的天空自由地飞翔,探索未知的领域,从而在多样化的思考中找到属于自己的路径和答案.