溯试题来路，析解题思路，明教学出路

［摘要］当前，新课标落实和全省中考统一命题成为初级中学面临的一大挑战，而如何开展试题研究、如何提高复习课教学的有效性则成为诸多一线教师面临的一大难题. 研究者以一道典型中考压轴题为例，通过试题评价、解法赏析及教学启示等维度展开全方位的剖析，力图为中考数学复习教学及试题研究探索一条行之有效的出路.

［关键词］中考数学；解法探析；高频错误；教学思考

全省中考统一命题，无疑是学校教学面临的一大挑战.新课标下的中考，除了考查学生基础知识、基本技能，更注重考查学生的思维过程、创新意识和分析问题、解决问题的能力，这也对初中教师的教学提出了更高要求.如何更加高效、更有针对性地开展中考复习教学，是一线教师一直在思考的问题.笔者认为，研究本省市近年来中考真题，体会命题思路和风格，关注中考已统一命题区域的中考试题，及时调整教学内容与教学方式，根据不同题型对学生进行有针对性的指导，多关注典型题、创新题、新考法试题、前沿性试题等. 下面，笔者就以2023年杭州中考数学第23题为例，围绕试题评价、解法赏析及教学启示等维度展开全方位的剖析，以期为中考数学复习教学探索一条行之有效的出路.

试题呈现

2023年杭州中考数学卷第23题（以下简称“本题”）：

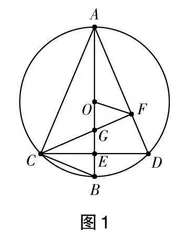
如图1，在⊙O中，直径AB 垂直弦CD于点E，连接AC，AD，BC，作CF⊥AD于点F，交线段OB 于点G（不与点O，B重合），连接OF．

（1） 若BE = 1，求GE 的长；

（2） 求证：BC² = BG·BO；

（3） 若FO = FG，猜想∠CAD的度数，并证明你的结论．

试题评价

1.核心知识与关键能力并行，凸显素养立意

本题是一道以圆为背景的综合题，不仅考查垂径定理、圆周角定理、全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的性质与判定等初中核心知识，还考查对学生借助几何直观先大胆猜想后小心求证的能力.本题重视发展学生分析问题和解决问题的能力，凸显数学学科独特的育人价值.

2.学习过程与数学理解交融，引领教学方向

本题背景源于学生所熟知的教材中的垂径定理模型，但又高于教材，是教材的变式、引申与拓展.同时也体现了考查的公平性，考查学生对数学概念与数学问题本质的理解与思考过程，引导学生关注自身学习过程，引领教师在教学中回归教材、返璞归真，挖掘教材例题、习题的教学价值，有效减轻学生的学业负担.

3.注重通法与淡化技巧互嵌，彰显学科价值

本题题干表述简洁明了，问题设置层次分明，知识衔接自然关联，同时在命制试题时巧妙地避开了模型化，注重通性、通法，淡化特殊技巧.尤其是第（3）问，在学生熟悉圆和三角形的基础上增加了条件“FO =FG”，此时需要挖掘题中隐含的数量关系，其中蕴含着丰富的数学思想方法，解法多元，彰显个性，将数学思维能力体现得淋漓尽致.

评析 由于本题中⊙O为定圆，从已知条件可判断出当点C，D，E，F，G中任意一点确定时，其余各点也随之确定， 再加上条件“FO =FG”，本题便已定型，接下来就是解形的问题，图中所有线段均可用含半径r 的代数式表示.解法7、8都是利用平行线截线段成比例的性质率先解出了线段AG，从而进一步求出相关线段之间的数量关系；解法9则是利用相似三角形的性质求出答案，与解法7、8有着异曲同工之妙.以上三种方法利用了多种“代数表达”刻画了同一个“图形结构”，充分体现了对几何图形的代数理解.

教学启示

1. 重视整体教学设计，提高学生的知识提取迁移能力

《义务教育数学课程标准（2022年版）》在课程实施的“教学建议”部分，首次提出了将单元整体教学作为能引发学生思考的教学方式，强调要“改变过于注重以课时为单位的教学设计，推进单元整体教学设计，体现数学知识之间的内在逻辑关系，以及学习内容与核心素养表现的关联.”

本题以圆为主要考查背景，不仅涉及圆自身的基本性质，还涉及相似三角形、特殊三角形等图形的性质，甚至可以用三角函数、代数推理等方法予以解决，对试题综合性的考查趋势已经不言而喻.因此，开展单元整体教学设计，挖掘知识间的内在关联已经迫在眉睫.

2. 关注几何基本图形，提升学生的几何直观素养

著名美国数学家和数学教育家G. 波利亚在《怎样解题》中指出：一个有用的念头，也许是个决定性的念头，它能使你一眼看出解决问题的途径.什么是波利亚所说的“念头”？笔者认为，对于“图形与几何”部分来说，就是几何基本图形.在审题过程中，学生若能快速识别并正确应用基本图形，就能快速地形成解题思路，实现数学思维能力的提升.

纵观本题所有的解题思路，几何基本图形几乎“形影不离”.无论是第（1） 问的“8 字型”，第（2）问的“母子相似模型”，还是解法1的等腰三角形“三线合一”模型、解法4的“四点共圆”模型、解法5的“A型”“X型”相似模型、解法8 的“角平分线模型”等都是学生耳熟能详的基本图形，教师在教学过程中要有意识地引导学生从千变万化的题目中总结共性，提炼基本图形并加以强化训练，在一题多解的同时做到多解归一，有利于培养学生恰当运用数学思想方法分析和解决数学问题的能力.

3. 倡导问题变式训练，培养学生的应用和创新意识

随着“双减”政策的实施，学生从大量的重复练习中解脱出来已是大势所趋，但同时又不能降低教学质量，变式教学或许是达成这一目标的有效方法.所谓变式，是指相对于某种范式（数学教材中具体知识、典型问题、思维模式） 的变形方式，通过改变问题的情景、条件、结论或者图形的关系，让学生自主探索，以激发学生的创新思维，从而更好地理解和掌握问题的本质规律.

至此，对这道中考压轴题的全方位解析也就告一段落，它带给我们太多的教学启示，也使今后的教学出路变得越来越清晰明了……面对全省统一中考命题的大背景，一线教师唯有立足新课标，以核心素养为导向，聚焦数学核心概念，重视知识整体关联，加强模型提炼，强化变式整合，在发展学生的思维品质上下功夫，鼓励学生大胆探究，敢于质疑，真正把课堂还给学生，突出学生的主体地位，进而实现立德树人的根本任务.