混乱与复杂之中的秩序和机遇

人类对于秩序有着天生的喜爱。无论是对于自己的生活，还是所研究的对象，如果可以让其进入到某种可以预期的、简单的循环之中，自然就会让人觉得稳定、安全、容易把握和理解。把一切复杂的事物都逐步分解，简化为简单的、可以预测的基本部分，由个体到整体，也曾经是科学家们最重要的研究手段。而那些看上去一团混乱、毫无规律可言、无法预测的混乱系统，则让人望而生畏。

摆脱“拉普拉斯之妖”

人类对于秩序的喜爱以及对于混乱的厌恶，除了天生的倾向之外，也与科学的发展过程有关。牛顿在17世纪创造了一套著名的经典力学体系。这个体系的思想非常深刻，但是其表达形式则相对清晰和简单，只使用一套微分方程便可以描述万事万物的运动规律。在牛顿的基础上又过了100年之后，人们的理性和完全理解自然界的信心，都得到进一步的发展，其标志性人物就是法国历史上最著名的数学家和物理学家之一：皮埃尔－西蒙·拉普拉斯（Pierre-Simon Laplace）。

拉普拉斯曾经热衷于为他的学生之一、法兰西的皇帝拿破仑·波拿巴，讲解数学理论和太阳系的结构。一次在听了拉普拉斯的讲述之后，拿破仑问道：在你的理论中上帝的位置何在？拉普拉斯充满自信的回答一直流传至今：“陛下，在我的理论中不需要这样的（上帝存在）假设。”

拉普拉斯在学术上活跃的时代大约比牛顿晚了一个世纪。他凭着自己在数学和物理学领域的才华，获得了“法兰西的牛顿”美誉。可以说，无论从学术传承还是从学术成果上来说，拉普拉斯都无愧于这个称号。如果说，牛顿在1687年出版的《自然哲学的数学原理》一书，首次让人类意识到了理性的力量，那么在大约一个世纪之后，“法兰西的牛顿”拉普拉斯在此基础上做出的成就则把人类对于自身理性的信心提高到了一个全新的程度。拉普拉斯撰写的五卷本《天体力学》（Mécanique céleste）极大地拓展了牛顿力学，通过严格的数学形式来描述天体的运动，勾画出一个秩序井然且稳定自洽的太阳系。

牛顿所构建的“绝对空间”和“绝对时间”之中的运动定律，实际上并非完全由数学所决定。在牛顿看来，神秘的万有引力就有着上帝神力的色彩，而整个太阳系能够以一种稳定的秩序运行，也绝非几条运动定律所能决定，大约是有隐形的天使在推动着天体运行。而在一个世纪之后，随着计算和观测更加精确，拉普拉斯证明整个太阳系的稳定状态并不需要神明或是天使的帮助，单凭由数学公式所规定的运动定律就可以维持其自身的稳定。正是因为有了这样前所未有的信心，拉普拉斯才首次把神明的位置排除在科学之外。

可以说，拉普拉斯一方面增强了人类对于科学和理性的信心，建立起没有上帝存在的决定论，另一方面也在无形中划出了科学和理性的边界。在他的描述中，科学应该是稳定的，有秩序且可以预测的。如果我们知道了一个系统的初始条件，我们就可以通过计算预测出这个系统在未来的任何发展变化，同时也可以计算出这个系统在过去任何一个时间的状态。也就是说，如果把整个宇宙看成一个整体，那么它就是一个永不出错的可以预测的机械。

在一个由确定性所主宰的世界中，每一粒被风卷起的尘土，它的每一个动作，都可以被计算出来。在拉普拉斯的眼中，整个世界就是这样一个可以被计算的，由一些运动规律和因果律所支配的世界。没有不确定性存在的空间，过去和未来，都可以通过计算被呈现在眼前。

从这种机械性的宇宙观出发，拉普拉斯假设存在某个“智能者”，他可以单纯地通过计算就知晓整个宇宙的过去和未来。拉普拉斯甚至效仿阿基米德说出了一句豪言壮语：“假设能知道宇宙中每个原子现在的确切位置和动量，智能者便能根据牛顿定律，计算出宇宙中事件的整个过程！计算结果中，过去和未来都将一目了然！”——后来人们将这个拉普拉斯想象中的超越时间束缚的“智能者”干脆称为“拉普拉斯之妖”。

在这种机械性宇宙观的基础之上，还原论思想也流行起来。哲学家笛卡尔就将自己的方法论描述为“将面临的所有问题尽可能地细分，细分至能用最佳的方式将其解决为止”，用简单来分解和解释复杂。著名科学作家侯世达在他的名著《歌德、埃舍尔、巴赫——集异璧之大成》中则这样解释：“还原论是对这个世界最自然的理解方式。它是说，如果你理解了整体的各个部分，以及把这些部分整合起来的机制，你就能够理解这个整体。只要是精神正常的人就不会反对还原论。”

从极小尺度到极大尺度，人类是否能够凭借着理性的力量，通过还原论方法，来理解这个机械性宇宙的所有方面？直到19世纪，人们仍然对此毫不怀疑。法国数学家奥本·勒维耶（Urbain Le Verrier）在1848年仅仅通过计算就预测了海王星的存在，将拉普拉斯的可预测的机械性世界观发挥到极致。有些数学公式固然难以计算，初始状态也难以知晓，但是人类仍然能够通过近似得以理解大自然的玄妙。例如复杂的空气运动，也在麦克斯韦和玻尔兹曼的努力之下，通过种种近似手段用统计方法得以被大致描述出来。到了19世纪下半叶，电磁学和统计力学相继诞生，科学的本质却没有发生太大改变，整个经典力学体系看上去更加稳固。人们对于理性的力量，以及预测整个机械性宇宙的信心更加充足。

这一切却在20世纪戛然而止。在20世纪初诞生的量子力学和相对论，让人们理解到在极小尺度下，人们对于一个系统的状态能够了解的程度存在着根本性的限制。测不准原理是大自然的基本法则之一；而在极大尺度上，所谓绝对时间和绝对空间并不存在，时空与物质相互作用。到了20世纪下半叶，人们进一步认识到，在极小尺度和极大尺度之间，也就是在人的尺度上，想要对一些复杂现象进行解释，还原论也失去了它的效力。如此看来，曾经显得神通广大的“拉普拉斯之妖”不可能存在。

进入到20世纪之后，人类通过还原论思想完全解释一个机械性宇宙的信心虽然受到了打击，但理性的力量却进一步增强。从20世纪下半叶开始，人类凭借着理性的力量拓展了科学的界限，深入到此前看上去混乱且不可预测的混沌之中，却从中发现了前所未见的秩序和美感。对于混沌和复杂系统的理解，是人类将对自然界和对自身的理解结合在一起的关键一步。从秩序到混沌，再从混沌之中寻找秩序——人类获得了一个更加生动且丰富的宇宙观。正是因为如此，现代人才普遍认为，量子力学、相对论和混沌理论，是人类在20世纪取得的三大科学突破。从天气预测到混沌系统

如果我们理解一个系统的运动规律，同时又掌握它的各个参数，那么我们是否能够在很大程度上通过计算来预测它在未来的状态？——与其说这是一个数学或物理学问题，不如说是一个哲学问题。从实际出发，我们不可能完全了解一个系统的运动规律，同时也不可能完全精确地掌握它的所有参数。即使是在牛顿和拉普拉斯的时代，人们也只能通过估计，进行大致的估算。问题在于，我们究竟能够在多大程度上保证预测的准确性？

天气预测是一个极好的例子。人们可以建立大气运动、冷热气流相互作用的数学模型，同时还可以通过测量，获得例如温度、湿度、气压等当时大气状态的参数。那么我们是否能够以此来预测之后当地天气的变化状况？从20世纪60年代开始，麻省理工学院的数学家和气象学家爱德华·洛伦茨（Edward Lorenz）最先开始了在这个领域的探索。

洛伦茨早在“二战”期间就为美国陆军航空军担任过天气预报员，这让他对天气预测产生了浓厚的兴趣。到了1961年，他开始尝试使用一台名为“Royal McBee LGP-30”的计算机来预测天气变化。“Royal McBee LGP-30”计算机有一台桌子大小，重量达到300多公斤，工作起来的声音类似于螺旋桨飞机，每秒钟能够进行60次乘法。洛伦茨建立了一个天气预测的数学模型，由12个公式组成。有了这台机器的帮助，洛伦茨把当前的天气数据输入进去，通过计算来预测几分钟之后的天气信息；随后再把这些数据输入，进行下一轮预测……逐渐累加，预测的时间长度就会逐渐从几天之后延展到几周之后。

这样的计算速度虽然在现代人看来如同儿戏，但在当时已经是难得的高科技，而且机器计算的结果要比人力计算更加可靠。在计算机的辅助之下，一个令洛伦茨迷惑不解的现象随之出现。在一次进行重复计算时，洛伦茨把之前已经得到的数据直接输入计算机——同样的数据，同样的算法，理应得到完全一样的结果，洛伦茨却惊讶地发现，他这次得到的天气预测结果与之前的结果在初期尚且能够保持大致相同，而预测的时间越远，则差距越大。

两次计算结果何以出现如此之大的区别？经过仔细检查，洛伦茨发现，自己在输入之前计算数据的时候，把原有的数字“0.506127”简化输入为“0.506”。就是这不到千分之一的差距，导致计算结果随后出现了极大的差异。这就与数学家们之前所想象的，初始条件微小的变化只会对结果造成微小的差异完全不同。这引起了洛伦茨的注意，他开始以数学家的眼光研究这个现象。

一种此前被认为超出了科学界限的全新领域，进入到科学家的视野之中。科学家们此前习惯于研究被微分方程等熟悉的数学形式所描述的线性系统，这种系统稳定，容易预测，而且初始条件的变化只会引起计算结果的微小差异。但是如果系统不能用简单的线性方程描述，一种更为复杂的非线性系统则会呈现出远超线性系统的复杂度——这种系统对于初始条件极为敏感，稍微变化就会导致随后计算结果的极大差异；另外，这种系统对于外来的干扰也非常敏感，受到一点干扰就可能陷入一种无序的状态之中。

在理论上，可以说这样的系统仍然是“可预测”的。根据描述这种系统的数学公式，只要人们能够非常精确地掌握其初始条件，仍然有可能对其进行计算。但问题在于，一方面这样的计算可能极其复杂繁琐；另一方面，人们的测量精度永远有限，而测量结果与实际结果的任何一点微小差异，都会导致随后预测的失败。

虽然洛伦茨是因为研究天气系统认识到了这种复杂系统的特点，但是对于数学家来说，需要用12个公式进行模拟的天气系统过于复杂，参数过多。洛伦茨需要找到一种相对简单的研究对象。他想到气流与水流的运动规律多有相似之处，于是设计了一种相对更加简单的动力系统——在一个盒子里面装满液体，盒子底部的液体温度更高，顶部温度更低，这样在盒子内部就会形成液体的流动——人们可以观测到在盒子的一侧热流以圆柱体的形状向上流动，在另一侧冷流则以圆柱体的形状向下流动。如果温差加大，水流还会形成摆动。相比之下，只需要一组分别描述流体力学、热传导和连续性的三个方程，就可以描述这个系统内部的水流运动规则。

经过对这个系统细致的研究之后，洛伦茨在1963年向纽约科学院提交了一篇足以载入史册的论文：《决定性的非周期流》（Deterministic Nonperiodic Flow）。这篇最终发表在《大气科学杂志》（Journal of the Atmospheric Sciences）上的论文标志着人类开始了对于“混沌现象”的深入研究。

实际上，要一直等到1975年，洛伦茨的研究才真正突破了天气研究领域的限制，成为一个受到全世界科学家关注的跨越传统学科的新领域。美国数学家和理论物理学家詹姆斯·约克（James Yorke）正式为这个学科命名为“混沌理论”（chaos theory）。

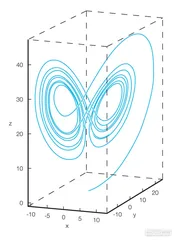
从20世纪60年代初开始，随着洛伦茨这篇标志性论文的发表，一个非常突出的形象以一种奇异的方式，不仅进入学术界，还进入了流行文化之中——这个形象就是一只正在扇动翅膀的蝴蝶。这源于洛伦茨在“相空间”中对于混沌系统的形象描述。

一个复杂的系统往往要受到多个参数的共同影响。为了研究系统的性质，研究者会把一个系统中的所有独立变量构成的空间叫做系统的“相空间”。相空间中的一个点，就对应系统的一个状态，对应一组给定的独立变量值。洛伦茨在研究这种会把初始条件的微小差异转变为巨大差异的复杂系统时，在相空间中绘制它的变化曲线，却在其中发现了一种奇特的美感。引用学者张天蓉的描述：“这是一个三维空间里的双重绕图，轨线看起来是在绕着两个中心点转圈，但又不是真正在转圈，因为它们虽然被限制在两翼的边界之内，但决不与自身相交。这意味着系统的状态永不重复，是非周期性的。也就是说，这个具有确定系数、确定方程、确定初始值的系统的解，是一个外表和整体上呈貌似规则而有序的两翼蝴蝶形态，而内在却包含了无序而随机的混沌过程的复杂结构。”

比利时数学物理学家达维德·吕埃勒（David Ruelle）在研究了洛伦茨通过电脑得出的类似于蝴蝶的图像之后，在1971年发明了“奇异吸引子”（strange attractors）一词。所谓“吸引子”（attractor），大约可以理解为一个系统的稳定状态。一个动力系统总有向稳定状态，也就是吸引子发展的趋势。在相空间的描述中，吸引子可能是一个点、一个环形，或是一个环面。而对于混沌系统来说，它的吸引子则成了标志性的类似于蝴蝶翅膀形状的具有两个核心的奇异吸引子。

英国数学家伊恩·斯图尔特（Ian Stewart）这样解释所谓“吸引子”对于一个系统的意义：“想象把一个乒乓球放到广阔的海洋里。如果把它放在水面以上，它会下沉；如果把它放到水面以下，它又会上浮。无论你把它放在哪里，这个乒乓球都会迅速地通过我们可以预见的方式移动到它的吸引子——海洋的表面。无论从哪里开始，乒乓球都会以一种可以预见的方式向它的吸引子——海水表面移动。一旦到达了海水表面，它就会在海水表面上下颠簸，陷入到一种混沌状态之中，但无论如何运动都会迅速回到海水表面。

尽管我们无法预测混沌系统如何运动，但是理解吸引子会让我们把预测的可能性缩小。我们还可以预测它一旦受到干扰离开吸引子之后又会如何运动。数学家们习惯用‘相空间’来描述系统。我们可以在相空间中放入一个点，之后观察它如何运动。在相空间里，一个稳定系统会像人们预期的一样迅速靠近吸引子（有可能是一个点，也有可能是一个简单的回路）。混沌系统也会向吸引子移动，但这不是简单的吸引子，而是‘奇异吸引子’，也就是我们看到的如蝴蝶翅膀形状的吸引子——扭曲、旋转，勾画出各种各样的形态。结合分形研究，人们越来越能够深刻理解系统倾向的行为。”

可能正是受到了混沌系统相空间图像的启发，洛伦茨在1972年的一次学术会议上做了名为《可预测性：巴西蝴蝶扇动翅膀会给得州带来一场龙卷风吗？》（Predictability：does the flap of a butterfly's wing in Brazil set off a tornado in Texas？）的报告，阐释他对于混沌系统的研究。这次报告的影响力超出了天气研究领域，在全世界的学术界引起了轰动。一个名词“蝴蝶效应”，从此进入大众文化之中——表示一个微小的因素有可能在后来导致极其重大的后果。而这也正是混沌系统最鲜明的特点。

如果我们对周围环境多加观察，会发现这种初始状态对随后系统发展的影响极大，同时容易受到外来因素影响的所谓混沌系统其实随处可见。在常人看来，混沌现象充满混乱与随机，不可预测。实际上如今我们讨论的混沌现象，并不等同于随机（randomness）。混沌现象与随机过程有关系，可以说它是随机过程和决定性规律的结合。虽然在20世纪后半叶之前，对于这些系统性质的研究超出了传统科学研究的范围，但其实在之前就早有科学家对此加以关注，并且意识到秩序、可预测性和混沌，三者之间的关系其实非常紧密。

在拉普拉斯出版《天体力学》大约100年之后，另一位法国数学家朱尔·亨利·庞加莱（Jules Henri Poincaré）开始注意到秩序与混乱之间的复杂关系。这源于瑞典国王奥斯卡二世在1887年发起的一项竞赛。这项竞赛涉及四个数学难题，其中一个难题就是关于太阳系的稳定性问题。

太阳系究竟是不是一个稳定的系统？答案在19世纪似乎是不言而喻的。拉普拉斯早在18世纪就曾经深入研究过这个问题，他最后得出结论，太阳系作为整体来说是一个稳定的周期性运动系统。

拉普拉斯的结论似乎并没有说服瑞典国王奥斯卡二世。在竞赛的激励之下，庞加莱对这个问题也进行了深入研究，并且初步得出了和拉普拉斯相同的结论。就在庞加莱获得了奥斯卡二世的奖金，并且即将出版自己长达190页的证明之时，他发现了自己证明过程中的失误，继而推翻了自己之前的全部结果，重新推出一个长达270页的证明，并且得出了一个完全不同的结论。

庞加莱发现，即使在理想状态下，忽略其他因素，只考虑牛顿力学的约束，一个复杂系统的运动状态也很难预测。如果只有两个物体，两者之间只受到万有引力的相互作用，运动状态倒还容易计算。但是哪怕在这两者之间只再加上一个微小的干扰因素，这三者之间的相互作用会迅速发展到过于困难而无法计算——这就是著名的“三体问题”。

在理想情况下，想要描述一个三体系统的状态并不算太困难，可以用一组9个微分方程进行描述。但是问题在于，想要对这个方程组进行精确的计算，进而对这个三体系统的运动状态做出精确预测，则会变得极其困难。庞加莱首先尝试在两个质量相似的系统之中引入一个相比之下质量极其微小的干扰因素。他发现，即便在这样的系统中，一点微小的干扰也会对整个系统的状态造成极大影响，更不用说当三个物体的质量相似时，即便给出初始状态，在三体相互吸引的情况下，系统也会很快陷入一种无法预测的混乱状态之中，几乎无法预测当时间趋于无穷大时系统的最终状态。后来庞加莱就这个问题发表了长达三卷本的《天体力学的新方法》（Les méthodes nouvelles de la mécanique celeste）。

细致研究了三体问题之后，庞加莱写道：“一种可能发生的情况是，初始条件的些微差异就会导致最终结果的巨大区别。先前的一个小错误会随后导致无穷的错误。这样也就无法进行预测。”庞加莱的研究也证明，如果从长远来说无可预测，那么其实我们通常认为互相对立的确定性和随机性，其实是相容的。

在19世纪，经过先行者庞加莱的研究，整个世界终于从一个拉普拉斯式的完全决定论描述中暂时挣脱了出来。庞加莱认为，想了解一个物理系统随着时间发展的变化，我们需要选择一套规则对它进行描述，建立模型，同时还要选择参数来描述这个系统。因为测量精度和干扰的问题，即使我们理解了整个世界的全部规律，随机现象仍然是无可避免的。

可能是因为走得太远，超越了自己的时代，在一个由传统力学和决定论主宰的年代，庞加莱对于拓扑学和混沌系统的研究在当时并没有受到太多的重视。直到他去世几十年之后，主要研究概率论、扰动、信息论和拓扑学的苏联数学家安德雷·柯尔莫哥洛夫（Andrey Kolmogorov）才在1954年首次重温了庞加莱的工作。

柯尔莫哥洛夫研究了外来干扰对一个系统周期性的影响。当系统受到干扰，物体的轨道可能陷入混乱，一个稳定系统便有可能演变为混沌系统。此时这种运动被称为遍历运动，只有能量参数守恒。在此基础上，一些苏联数学家们发展了遍历理论。又过了几十年，对于混沌理论的研究才开始引起全世界各个领域科学家的关注。

在混沌理论中，秩序和混沌并非对立，而是形成了一种奇异的混合体。在不可预测和混沌的行为之中，可能还隐藏着一种极为严格的秩序。蝴蝶效应就是混沌系统的一个标志。这种看起来的随机性其实与经典力学的确定性原理并不冲突。只不过系统随时随地都有着人们根本无法察觉的细微改变而已，而这些细微的改变又有可能是系统未来发展的决定性因素。

蝴蝶效应说明，一个混沌系统会迅速放大初始条件的差异。比如说系统发展的两条轨道在初始时距离为D，那么在经过这个系统出现混沌特征所需要的时间，也就是“李雅普诺夫时间”（Lyapunov time）T之后，它们之间的距离会变成D的10倍。正因为如此，目前最先进的天气预报系统也只能预测大约一周之内的天气情况，而在50年前，人们只能预测18个小时之内的天气情况。

在庞加莱对非线性动力系统的行为进行研究一个世纪之后，在洛伦茨等学者的努力之下，对于决定性的混沌的研究，或者说混沌理论才开始被建立起来。此后，混沌理论开始对全世界各个领域的研究都带来了巨大的影响——这种现象本身看上去似乎就是一种混沌。生物学家、经济学家、社会学家、医学专家……都开始称自己为混沌学专家。混沌理论与几何的结合

进入到现代社会之后，尤其是想要通过科学手段研究混沌现象，就需要超越人们的直觉，找到科学方法和科学语言。通过对混沌系统越来越深入的研究，人们发现可以通过一种几何语言对混沌系统进行非常精确的描述。同时，人们正是凭借对混沌系统不断深入的认识，才开始进入一个全新的领域，开始了对复杂系统的研究。

对于混沌理论的研究，往往需要大量远超人力所及的计算。因此人类对于混沌现象的理解，随着计算机时代的到来而不断深入。同时，随着计算机技术的发展，新的数学分支出现了。人们发现在数学的不同领域之间，也产生了奇妙的联系。混沌系统的内在结构，以一种清晰的形式和全新的视角被展示出来。

法国数学家本华·曼德博（Benoit Mandelbrot）在1973年发表了曼德博集合（Mandelbrot set），这是一种新型的几何语言——分形（fractal），分形最大的特点就在于对相似形式的不断重复，因此其局部与整体呈现了相似性。分形现象在自然界中随处可见。比如说，云彩的一小部分看上去就像整片云彩，一块石头的形状看上去与一座山无异。在生物体中，例如我们所熟悉的花菜的形状，一些植物的叶片，一些国家海岸线的形状，以及支气管树（bronchial tree），都是明显的分形。

脱离了传统欧几里得几何的限制，只是通过简单的形式和无限的重复，借助计算机，分形展示出了一个神奇的几何世界，把有限和无限联系在一起。例如著名的科赫曲线（Koch curve），从一条直线开始，按照简单的规则，就能构建出无比复杂的图形。

曼德博随后发现，其实洛伦茨吸引子本身也是一种分形结构，而且还可以通过分形的几何语言定义其吸引子的维度（dimension）。比如说，科赫曲线的维度大约是1.26，洛伦茨吸引子的维度大约是2.06。从奇异吸引子的形状及几何性质，我们看到了混沌和分形之间的内在联系——分形就是混沌的几何表述。

在此之上，借助分形这种全新的几何语言，人们对于维度有了全新的认识。此前要描述一个几何体的维度，人们大多通过自己对于空间的本能感觉，用一个整数加以形容。例如一条直线的维度是1，一个平面的维度是2，一个圆球的维度是3……但是通过分形语言，人们发现可以用非整数来描述维度。可以说，通过分形，人类对于空间本质的理解加深了。

只要细心观察，就会发现自然界中其实更为普遍的是复杂的非线性系统。人们只是利用简单的线性系统对其进行模拟，有些可以起到一定的效果，有些则注定失败。总之，想要深入理解这些自然现象，就必然要用到混沌理论。比如人体的很多器官在通常状态下都是以可预测的线性行为进行工作的，人们也可以以此来解释很多现象，例如动脉收缩会导致血压上升，心脏附近的血管堵塞可能导致心绞痛……但在这些显而易见的事实之下，还隐藏着更为复杂的规律。经过研究发现，生物体可以增加自身的复杂度，或者说，生物体自身就包含着复杂的混沌系统。研究人的血液系统、大脑和呼吸系统，科学家们都观察到了这个现象。

心跳的节奏对初始条件非常敏感。实际上，人类的心脏由数百万个细胞构成，在通常状态下，它虽然有节奏地收缩和放松，却是一个标准的混沌系统，具有复杂的吸引子。实际上，没有混沌现象，心脏系统就无法正常工作，因为心脏也需要利用混沌系统的自组织功能来满足心脏对生命体的需求。心脏细胞共同工作，同步收缩和放松可以形成健康的心跳。这种同步的工作状态是系统的吸引子，但并不是唯一的吸引子。如果心脏跳动受到干扰，就可能出现心房颤动——这是心脏的另一个吸引子。而所谓的体外除颤器（AED），就是要给心脏一个足够大的电压，让心脏从混沌系统中回到健康的心跳吸引子。

生物体中混沌系统的例子数不胜数。除此之外，回顾当年牛顿、拉普拉斯和庞加莱都研究过的问题，在我们看来，井然有序的太阳系其实也是一个混沌系统——这是人类认识的第一个混沌系统。太阳系中的各个天体之间通过引力相互影响的复杂程度远超过三体问题。在太阳系内部运行的行星，除了受到相互之间引力作用的影响之外，还受到不断从太阳系外部进入到内部的小行星的干扰。因此，就像对天气系统的预测一样，想要对太阳系内天体轨道进行长时间的预测是不可能的。人类最多只能对1000万年之内的太阳系状态进行预测。

作家林登·皮尤（Lyndon Pugh）在2007年写道：“混沌理论的关键点在于它强调了对环境的敏感性，不确定性代表着机会。”一个难以预测的混沌系统，如果具有足够的复杂度，这种复杂系统就有可能展示出简单的线性系统所没有的现象。通过对混沌系统的研究，结合其他领域的研究进展，人类开始进入对复杂性科学（complexity science）的研究之中。一个更为复杂，也更加广阔的领域展现出来。它不仅深刻影响了人类对自然科学的认识，也影响了人类对社会科学，包括对自身的认识。因此，著名物理学家史蒂芬·霍金曾经说：“21世纪将是复杂性科学的世纪。”

加拿大数学家布莱恩·古德温（Brian Goodwin）这样描述复杂性科学研究对于整个西方科学思想的影响：“复杂性理论正在成为一门认识和庆祝大自然创造性的科学。它非比寻常，因为它开启了一个让我们认识世界的新方法，让我们理解复杂动力系统对于初始条件敏感，并且具有涌现性。从微生物系统到整个生物圈，我们必须与这些与我们的生活息息相关的复杂系统谨慎相处，因为我们不能控制它们，却可以影响它们。这对于整个西方科学界都是一种新思想。”

关于复杂系统，可以简单把它描述为含有许多个相互作用的变量的系统。复杂系统同样非常常见。例如由数百万只蚂蚁组成的蚁群，以及主要由神经元构成的大脑等，这些系统的基本单元之间的交流方式都比较相似，但是当其以巨大的数字组成一个充分复杂的系统，那么整个系统便可能展示出单个个体所不具备的智能——这就是所谓的“涌现现象”（emergence）。科学家们曾经依赖的还原论思想不再适用，这也就要求科学家们发展出一种全新的研究方法。

物理学在很大程度上是建立在可控和可重复的实验基础之上。在还原论思想的指导下，一个复杂的整体等于每个简单部件的总和，但是复杂系统则会呈现出简单系统所没有的规律。在缺少一个中央控制机制的情况下，凭着复杂系统自身的性质，就可能会出现例如“自适应”“自组织”等看上去非常奇特的现象。涌现、自适应、自组织等名词，也随之成为了人们在混沌理论的基础之上，研究复杂性科学的常用名词。例如木星大气层上巨大的大红斑已经有至少400年的历史，这是一个典型的复杂自适应系统呈现出来的稳定结构。而科学家们估计生命现象在地球形成之后大约5000万年就开始产生于原始海洋，这本身也是复杂自适应系统进行自我复制的例子。

正是因为混沌现象以及复杂性系统在自然界中无处不在，如果我们回顾前人的努力，其实对这类现象背后的科学原理进行的研究早已有之。除了庞加莱对于混沌系统的研究之外，英国计算机专家和数学家阿兰·图灵（Alan Turing）也曾经研究过，通过反应和扩散的协同作用，可能造成复杂系统中某种不均匀模式的聚集和重复。这种机制可以解释生物体的某些现象，而且这类影响可以非常精确。这种自组织形式的化学反应可以解释斑马皮肤条纹的形成。

图灵的研究论文《形态发生的化学基础》（The Chemical Basis of Morphogenesis）早在1952年8月就发表在英国皇家学会的刊物《哲学汇刊》（Philosophical Transactions of the Royal Society）上。图灵在论文中通过数学方法证明，整个系统在一点催化的作用下，就可能发生自组织现象。在当时，图灵研究的重要性同样没有在科学界引起应有的重视。后来人们才发现，图灵的理论可以用来解释自然界中很多图案的形成。研究者们甚至在纳米级的微观结构里都观察到了这种图案。人们给这种图案命名为“图灵斑图”（Turing pattern）。

不仅人体组织，由人所组成的人类社会也是标准的复杂系统。认识到这一点之后，关于复杂性科学的很多成果立即被应用到人文领域。进入21世纪之后，一些复杂性研究领域的名词，如“复杂适应系统”“涌现行为”“自组织”“系统韧性”“适应性非线性动力学”，开始被大量合适或不合适地挪用到社会科学之中，尤其是商业领域。

有人认为股市的涨落与水龙头中滴下水滴的模式有相似之处，可以试着以此进行预测。混沌理论也被用于公司管理，比如说一家公司就是一个标准的非线性系统，一个单独个体的行为很可能对整体产生巨大的影响，而看似巨大的变动可能反而没有太大的效果。从这个角度出发，从远距离观察一个组织（公司）的行为模式，而不是聚焦于具体事件或个人，也可以更有效地管理公司，同时保留一定的自由度，让公司进行自我管理。

有管理学研究者认为一家公司的最佳状态就是出现有限的混乱。这样既可以保持公司的创造力，不陷入死气沉沉的有序的静止状态，同时也不至于让整个公司无法控制，陷入到无法预测的彻底无序。让员工自由发挥，出现自组织现象，同样可以让公司保持创造力和进化的能力。可以说，从混沌理论和复杂性研究都可以看出，公司管理需要有效的领导力、长远的眼光、强有力的价值观和开放的沟通能力。

甚至有人把混沌理论研究引申到人生哲学的高度。例如在《混沌理论的七节人生课》（Seven Life Lessons of CHAOS）一书中，几位有科学研究背景的作者甚至从中总结出了关于人生的数条哲理，这大概算得上是新型的心灵鸡汤了。

从人类认识到混沌系统，对它进行深入研究，把它与物理学和几何学相联系，直到进一步展开对复杂性科学的研究，可以说从20世纪下半叶开始的这一系列开创性研究，都难以用人类传统的学术方法进行定义或分类。混沌理论，复杂性科学，都具有跨学科、拥有广泛应用性的特点。人类此前在不同领域的科学研究，往往对研究对象是生物还是非生物有着明确的界限。要知道，生命现象正是在复杂系统中涌现出来的一个奇迹。复杂性科学的发展，有助于帮我们跨越生命和非生命现象之间的鸿沟。我们对于复杂性的理解越深刻，也就进一步加深了对自身的理解。

〔参考书目：《蝴蝶效应之谜：走近分形与混沌》，张天蓉著；《混沌：开创一门新科学》（Chaos：Making a new science），詹姆斯·格雷克（James Gleick）著；《复杂》（Complexity），梅拉妮·米歇尔（Melanie Mitchell）著；《规模》（Scale），杰弗里·韦斯特（Geoffrey West）著〕 混沌科学庞加莱牛顿自组织牛顿力学数学家数学混沌理论混沌现象拉普拉斯方程时间计算拉普拉斯