喷注方案对CH4-O2旋转爆轰发动机冷流掺混特性的影响

摘 要：      旋转爆轰发动机是一种可自增压、 持续提供推力的新概念发动机， 在航空航天领域具有远大的应用前景。 喷注结构是旋转爆轰发动机设计的基础， 为研究不同喷注方案下发动机内流场的演化过程， 本文选取模型为双侧喷注的环形燃烧室， 通过求解三维雷诺时均N-S方程， 针对喷孔直径与旋流喷注角度变化开展了一系列冷流场研究。 结果表明： 增大喷孔直径将有利于提高燃料射流动量， 增加燃料径向穿透深度， 促进推进剂组分的扩散与混合； 增大旋流喷注角度将使得燃料射流动量下降， 气流沿径向发生显著偏折， 降低混合效率。 低喷注动量的燃料射流难以与氧化剂主流充分掺混， 受气流冲击影响严重， 表现出沿燃烧室内外壁面分布的特性， 在流场中心形成带状的低浓度区， 最终导致混合不充分现象。

关键词：     旋转爆轰； 喷注结构； 掺混； 喷孔直径； 旋流

中图分类号：       TJ760； V231

文献标识码：    A

文章编号：     1673-5048（2025）01-0099-08

DOI： 10.12132/ISSN.1673-5048.2025.0002

0 引  言

旋转爆轰发动机（Rotating Detonation Engine， RDE）是一种可在封闭构型燃烧室内旋转自持的新型发动机， 具有热循环效率高、 无需重复点火、 组合形式多样等特点。 该设计理念由Voitsekhovskii^［1-2］在20世纪50年代率先提出， 并于60年代在盘型燃烧室内首次实现了旋转爆轰的成功运行。 此后， Bykovskii等^［3-4］与Nicolls等^［5］分别就爆轰于喷气推进领域的工程应用潜力进行了一系列探索研究。 时至今日， RDE已然成为新概念推进领域的研究热点， 有望成为下一代高超声速推进动力的备选方案， 美国、 俄罗斯、 日本、 德国、 法国等国家均针对旋转爆轰开展了大量相关研究。

经典爆轰物理理论认为， 作为燃烧波与激波的高度耦合现象， 爆轰波的前导激波后将会因横波反射而产生鱼鳞状结构^［6］， 并由此衍生出胞格概念。 胞格尺寸对爆轰波的形成与发展机制起到至关重要的作用， 尺寸越小， 反应活性越高、 可爆性越强。 此参数对爆轰混合物当量比的变化较为敏感， 根据Aminallah等^［7］的试验结果， 对于本文采用的CH4-O2混合气， 其在120 kPa和293 K条件下的胞格尺寸在当量比0.76与1.09时分别为3.49 mm与2.09 mm， 爆轰性质存在显著差异， 可见燃烧室内混合气的局部当量比分布不均匀将对爆轰发动机特性产生巨大影响； 并且， 在现有RDE试验^［8-10］中， 已广泛观察到燃烧室内旋转传播的爆轰波将与喷注结构相互作用， 由此导致的包括集气腔压力振荡与声学耦合在内的诸多现象将深刻影响爆轰波起爆与自持。 由此可知， 喷注结构与相应参数的设计是RDE研究的基础， 良好的抗反压性能与燃料掺混特性有助于旋转爆轰波在燃烧室内的起爆与自持传播^［11］， 也有利于拓宽自持工况范围。

由于仿真可直观获得全流场数据， 目前针对喷注与混合过程的研究以二维与三维数值模拟为主。 Schwer等^［12-13］通过二维仿真探索了喷注面积与几何形状对旋转爆轰的影响， 在集气腔中观测到了与爆轰波同频的压力振荡， 且振幅随喷注面积增大而增加。 徐雪阳等^［14-15］使用三维非预混数值模拟， 全面分析了质量流率、 当量比等喷注参数与喷注位置、 角度、 单双侧喷注等喷注结构对混合效果影响的作用机理。 Weiss等^［16］采用雷诺平均方程（Reynolds Average Navier-Stokes， RANS）详细研究了高速射流、 回流区、 涡旋如何作用于混合过程。 Lietz等^［17］在大涡模拟（Large-Eddy Simulation， LES）的基础上开展了高保真数值模拟， 注意到喷注参数改变将显著影响爆轰前沿， 并导致小尺度变化的发生。 Kou等^［18］针对喷注孔间距的变化开展了试验研究， 引入无量纲参数并确定了其最优值， 总结了更改当量比导致的不稳定爆轰工况范围变化的规律。

根据Bykovskii等^［4］提出的公式， 爆轰波在燃烧室内稳定传播条件需满足波高大于等于临界高度， 即喷注结构在爆轰波扫掠后必须迅速恢复喷注以维持可燃混合气累积层高度， 使得旋转爆轰得以自持。 然而， 爆轰波在燃烧室内以高度非定常的形式自持， 喷注结构与爆轰波的相互耦合将导致一系列不稳定爆轰现象； 旋流喷注则可使得部分喷注动量与爆轰传播方向平行， 减少波头的高度波动， 一定程度减弱瞬时传播特性的不稳定。 Zhou等^［19］设计了偏转角度为60°的旋流喷注结构并通过试验研究了煤油/掺氢空气在此条件下的爆轰性质， 观察到大量的模态转换、 低频振荡与零星爆轰等不稳定现象。 Shao等^［20］通过二维数值模拟针对不同旋流喷注角度作用于旋转爆轰波的影响进行了仿真， 认为在波高不受明显影响的前提下， 旋流喷注使得反应区恢复填充的混合气更加均匀， 减轻了推进剂消耗速率的振荡， 并观测到爆轰前沿区域开尔文-亥姆霍兹不稳定性的明显改善， 可知旋流喷注更有利于爆轰波稳定自持。

推进剂混合特性是旋转爆轰起爆与自持的基础， 喷注结构的变化将直接影响燃烧室可爆性、 爆轰效率与传播稳定性^［21］。 目前， 基于双侧喷注构型的喷注孔径变化研究尚显不足， 亦未存在可显著改善爆轰不稳定的旋流喷注方案， 冷态旋流流场下燃料与氧化剂的分布特性亟待深入研究。 为深入研究高效喷注掺混方案， 并为旋流喷注下旋转爆轰发动机流场分布提供参考， 本文拟针对喷注孔径与旋流喷注角度的变化开展三维冷态流场数值模拟研究。

1 计算模型与方法

1.1 物理模型

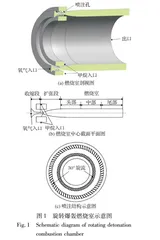
本文采用的旋转爆轰发动机模型如图1所示， 其中， 氧气为环缝进气， 甲烷为小孔进气。 氧化剂经过收缩-扩张的Laval结构进入燃烧室， 在扩张段壁面均匀分布着若干对称的燃料喷注孔， 内外环集气腔内的甲烷由此注入燃烧室中。 发动机扩张段长20 mm， 燃烧室长度为60 mm， 燃烧室内外半径分别为30 mm与38 mm， 氧气喷注喉部宽度为1.2 mm。 基于发动机设计参数与流量要求， 选取的喷孔直径为0.8 mm， 0.6 mm与0.5 mm， 并在改变喷孔直径时通过增加喷孔数量保持总喷注面积不变， 达到控制变量的效果。 旋流喷注下， 燃料喷孔则将与氧气来流成图1（c）所示的夹角， 图中夹角为30°。 由于较小的旋流角度对流场周向动量影响较弱， 较大的旋流角度将使得气流与设计工况下的轴向马赫数偏差较大， 无法充分形成对照， 参照Shao等^［20］对旋流角度变化的研究， 本文选定的旋流角度为30°， 45°与60°。 本文各算例对应的喷孔直径d与旋流喷注角度α如表1所示。

1.2 计算方法

本文对喷注混合过程进行了三维全流场数值模拟， 采用隐式Coupled求解器进行稳态双精度求解； 对流通量采用Roe格式分解； 动量方程、 湍流方程以及能量方程的离散格式均为二阶迎风格式。 数值解收敛标准为各项残差值下降三个数量级， 且入口与出口流量达到定常。 对热力参数使用NASA分段多项式拟合每一种组分的比热， 采用分子动力学理论计算各组分的导热系数与动力粘度， 再利用理想气体混合定律确定混合气的热力性质。

1.2.1 控制方程

本文将针对有粘的Navier-Stokes方程进行求解， 包含如下所示的连续性方程、 动量方程与能量方程：

ρt+Δ·（ρV）=0（1）

t（ρV）+Δ·（ρV）=Δ·σ+ρg（2）

t（ρCpT）+Δ·ρCpTV=Δ·（λΔT）+DpDt+D+

V·ρF（3）

式中： ρ为流体密度； V为速度矢量； σ为表面力； g为体积力； Cp为定压比热容； T为流体温度； λ为导热系数； D为粘性耗散项； F为体积应力。

1.2.2 湍流方程

非预混条件下， 粘性是影响喷注混合过程的重要因素， 本文采用SST k-ω两方程模型^［22］计算， 该模型在远场采用k-ε模型， 壁面附近激活k-ω模型， 并通过混合函数实现模型的切换。 方程具体形式如下：

DρkDt=τijuixj－β*ρωk+xj（μ+σkμt）kxj（4）

DρwDt=Yvtτijuixj－βρω2+xj（μ+σωμt）ωxj+2（1－F1）ρσω21ω kxjωxj（5）

式中： k为湍流动能； ω为湍流耗散率； ui为速度分量； μ为动力粘度； μt为湍流动力粘度； vt为k与ω之比值； Y， β， β*， σk， σω， F1均为模型参数， 具体取值同Menter^［21］一致； τij为雷诺应力张量， 定义为

τij=μtuixj+ujxi－23ukxkδij（6）

式中： δij为克罗内克尔符号。

1.3 边界条件

本文中的各算例采用相同的气动参数， 计算模型包含甲烷与氧气两组压力入口， 绝对压力分别为709 275 Pa与607 950 Pa； 出口绝对压力的选择则考虑应用环境而选为50 000 Pa； 壁面均选为无滑移绝热壁； 边界温度均为300 K； 计算初始化将从氧气入口开始， 并填充300 K、 0.1 MPa的氧气。 具体计算参数如表2所示。

1.4 无关性验证

本文采用六面体与分层多棱柱（Poly-Hexcore）方法进行网格划分，并对喷孔区域采取局部加密以提高算例的可靠性， 网格示意图如图2（a）所示。 分别使用3套网格进行无关性验证， 网格数量分别为102万， 184万和295万， 燃烧室主流区域平均尺寸约为0.8 mm， 0.6 mm和0.4 mm， 具体无关性验证结果如图2（b）所示。 由图可知， 燃烧室中轴线的马赫数在加密后波动较小， 中等网格与细网格下燃烧室主流区马赫数间的偏差不超过2%， 甲烷浓度偏差不超过0.5%， 捕捉到的流场结构与波系基本一致。 结合网格精度， 出于计算资源考虑， 本文最终选用中等尺寸网格对流场进行划分。

2 计算结果与讨论

本文将参考以下无量纲参数以确保可充分衡量各工况下的掺混性能。 引入混合效率η（z）^［23］以充分描述推进剂混合状况：

η（z）=c′CH4·ρω·dxdycCH4·ρω· dxdy（7）

式中： ρ为混合气密度； ω为轴向速度； cCH4为甲烷质量分数， 可发生反应的甲烷浓度c′CH4定义为