面向增材制造的进气道拓扑优化数值研究

摘 要：      进气道是冲压发动机的重要部件之一， 其强度与刚度对于冲压发动机稳定性至关重要。 为降低发动机消极质量并优化发动机设计， 本文以某进气道为研究对象， 在满足进气道变形和承载要求的基础上进行进气道薄壁结构减重设计。 对进气道进行静力校核， 根据进气道在4种工况下的初始强度校核结果确定优化设计域， 结合点阵结构， 同时考虑加强筋布局优化与加强筋尺寸优化， 运用变密度拓扑优化方法， 采用主级加筋结合局部点阵加筋填充的优化方案对进气道进行了优化设计。 利用有限元软件进行优化前后强度、 刚度、 稳定性校核， 优化后进气道结构质量减少了8%， 稳定性增强， 整体刚度分布更好， 实现了进气道的减重与结构设计空间的扩展， 证明本文采用的优化方法可行性。

关键词：     拓扑优化; 数值研究; 进气道; 点阵结构; 薄壁加筋;  冲压发动机

中图分类号：     TJ760； V431

文献标识码：    A

文章编号：     1673-5048（2025）01-0107-08

DOI： 10.12132/ISSN.1673-5048.2024.0193

0 引  言

拓扑优化技术作为结构优化设计的重要分支， 是结构轻量化设计、 获得高性能创新构型的有效设计方法， 现已被广泛应用于航空航天领域中^［1-2］。 降低消极质量是优化发动机设计的有效方法， 因此工程上正在寻求对发动机各部件进行减重设计。 薄壁加筋结构是航空航天装备中的常见主承力构件， 进气道也具有典型的薄壁特征。

加筋板壳结构因其良好的力学性能受到了越来越多的关注， 其结构特点是板壳结构和加强筋的结合。 目前针对该结构已有大量优化方法， 基结构法最先被提出用来解决各种加筋板壳结构优化问题^［3］。 Zegard等^［4］将基结构法引入到多种平面几何结构进行拓扑优化。 牛斌等^［5］采用基结构法作为主要工具， 将结构动柔度设定为优化的目标函数， 成功地完成了阻尼与加强筋布局的协同优化设计。 丁晓红等^［6］提出了自适应生长设计法， 该方法设定最小柔顺度为优化目标来优化加强筋的布局和轮廓。 Li等^［7］根据叶脉形成的原理， 提出一种仿生优化设计方法， 以结构应变能和第一阶固有频率的权重函数为目标函数， 对加筋板壳结构进行布局优化设计。 滕晓艳等^［8］基于植物脉序分枝结构特性， 以谐振结构声辐射功率为目标函数， 对薄板结构中加强筋布局优化设计。 Zhou等^［9］基于渐近均匀化法和变密度法对筋条单胞优化设计， 提高加筋结构屈曲承载性能。 Feng等^［10］基于变密度法和B样条曲线参数化法， 以柔顺度最小化为目标， 实现加强筋的布局和截面优化设计。 Huang等^［11］提出了一个新的工程方法， 该方法包括了离散和连续设计变量， 并通过构建分支多点函数来近似优化问题， 使优化问题显式， 从而实现了加筋板壳结构加强筋布局和尺寸优化设计。 目前， 对加筋板壳结构优化问题主要集中在对加强筋布局的优化设计， 考虑加强筋尺寸的优化设计还较少。

本文同时考虑加强筋布局优化与加强筋尺寸优化， 运用变密度法拓扑优化方法并结合点阵结构进行了优化设计， 在拓扑优化计算结果的基础上对局部结构进行点阵加筋填充， 满足进气道变形和承载需求， 有效扩展了结构设计空间， 在保证原刚度和强度的基础上进行进气道的减重设计， 提高材料的利用率。

1 物理模型及优化方法

1.1 物理模型

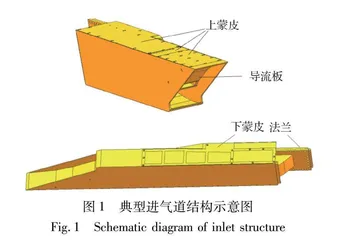
图1为典型进气道结构示意图，  由进气道主体、  上蒙皮、 下蒙皮、 导流板等组成， 其中上蒙皮、 下蒙皮布置在进气道的上下表面， 导流板位于进气道主体内部的流道中。

1.2 优化理论

（1） 单约束优化算法

本文采用Liu等^［12］在传统SIMP法基础上发展的改进算法， 其表达式为

Ei（ρi）=Emin+ρpi（E0－Emin）（1）

式中： p为给定的惩罚因子； Ei（ρi）为映射单元的弹性模量； ρi为单元伪密度； E0为材料的弹性模量； Emin为给定刚度最小值， 通常取0.000 1， 避免刚度矩阵的奇异解问题。

基于SIMP材料惩罚模型^［13］， 以最小化柔顺度作为优化目标， 体分比为约束， 建立拓扑优化列式为

find： X={ρ1， ρ2， …， ρN}T

min： C=uTKudΩ

s.t. Vc－Vmax≤0

0≤ρi≤1（2）

式中： ρi（i=1， 2， …， N）为单元伪密度； Vc为设计域结构体积分数； Vmax为体积约束； C表示结构柔顺度。

（2） 多约束优化算法

MMA算法^［14］对拓扑优化问题有着良好的稳定性和适应性， 且在求解多约束问题有着更优秀的表现， 因此选择数学规划法中的MMA算法作为本文优化求解方法， 对式（2）增加约束， 具体形式为

find： X={x1， x2， …， xn}T

min： f0（X）

s.t. fi（X）≤f^maxi，  i=1， 2， …， m

x^minj≤xj≤x^maxj， j=1， 2， …， n（3）

式中： X为设计变量； x^maxj为设计变量上限； x^minj为设计变量下限； fi（x）为设计变量x对应的约束值； f^maxi为上限约束； m为约束数量； f0（x）为目标函数。

基于上述公式， 初始化或更新单元设计变量， 将子问题解重复迭代， 直到满足优化目标或者达到设置迭代步数后停止。

（3） 薄壁加筋结构的多约束

对于薄壁结构加筋的拓扑优化， 需要进一步的改进。

加筋结构需要两方面的约束：

（a） 冲压约束， 即变量单元的密度在薄壁结构的厚度方向上保持恒定。 由于厚度方向与单元的几何信息密切相关， 为实现冲压约束必须构建单元和单元之间的关系， 这对结构化网格是较为直观的。 然而， 对于非结构化网格的结构， 单元的几何信息和薄壁结构厚度方向没有明显的关系， 从而导致冲压约束的可用性差。

（b） 尺寸约束， 拓扑优化结果往往使单元密度堆积在传力路径上， 尽管这种设计在理论上表现良好， 但是在实际生产过程中却面临诸多挑战， 或者与预期的结构性能存在显著差异。 为了获得筋条形式的拓扑优化结果， 需要控制单元既不能生成孔洞， 也不能大量堆积， 因此需要孔洞尺寸约束以及最大尺寸约束。 最大尺寸约束的表达式为

∫Ωr（y）ρ（x）dΩ＜∫Ωr（y）dΩ  （y∈Ω）（4）

式中： 等式左边表示单元质心为半径测试域Ω的总体积， 右侧表示约束的总体积。 对于任意单元e， 其测试域的表达式为

x∈Ωer if x－x－e≤rmax（5）

孔洞尺寸约束的表达式为

∑i∈Revi（1－ρi）η≥V^emin（6）

式中： vi为单元体积； V^emin为测试域最小空隙体积约束； 参数η控制灰度单元被认定是空隙的程度。 通过孔洞尺寸约束以及最大尺寸约束， 可以保证拓扑优化结果在冲压约束下构成加筋形式， 对后续复杂薄壁结构的加筋约束提供面内约束的技术基础。

另外， 为了解决拓扑优化求解过程中可能遇到的棋盘格问题和网格依赖性求解问题等， 本文采用各向异性Helmholtz过滤方法^［15］来求解算法方程， 避免了大量网格信息的获取步骤， 可以更好地实现冲压约束， 这对复杂薄壁结构的拓扑优化有重要优势， 可以大大加快收敛进程， 并且对网格划分的质量依赖更小。

密度过滤由滤波函数和密度的卷积实现， 表达式为

ρ～（x）=（Fρ）（x）=∫BRF（x－y）ρ（y）dy（7）

式中： F为线性卷积核； BR为以该网格中心点为中心半径的圆形区域； ρ～为过滤后的密度， 即最后用于计算弹性模量的密度。 对于滤波函数有

∫BRF（x）dx=1（8）

卷积积分在离散情况下采用表达式为

ρ～j（x）=∑i∈Ne， jω（xi）viρi∑i∈Ne， jω（xi）vi（9）

式中： 权函数ω（xi）随距离线性或指数增大。

在实际有限元计算的应用中， Helmholtz方程可写为

ΔTKdΔρ～+ρ～=ρ（10）

式中： Kd为正定的张量， Kd=r2r2r2， r为过滤半径尺度。

通过修改Kd的过滤半径， 使沿薄壁结构厚度方向设置远大于其他方向的过滤尺寸， 就可以实现在不借助相邻坐标信息的前提上实现冲压约束， 利用该特性， 建立复杂薄壁结构的加筋描述方法^［16］。

1.3 优化流程

进气道优化流程如图2所示。 首先， 确定进气道的优化目标， 构造优化问题的目标函数与约束函数， 建立进气道的有限元模型， 根据材料属性、 约束边界条件、 载荷边界条件、 连接关系等信息对其进行有限元静力校核， 根据计算结果确定优化设计区域， 而后进行优化设计域的拓扑优化计算工作。根据装配关系同时参考有限元仿真结果， 从而确定优化设计区域及优化模型， 而后进行优化设计域的拓扑优化工作。 根据得到的拓扑优化结果重构几何模型， 并对重构后的模型进行静力校核， 比较优化前后结构的强度、 刚度与稳定性， 迭代优化， 直至满足设计要求。

1.4 优化方案

将侧壁设计区域简化为500 mm×150 mm的平板作为验证算例， 四边简支， 一面受均布压强作用， 厚度方向划分10层网格， 进行初始结构静力校核分析； 屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷， 以线性失稳特征值作为表征， 特征值越大说明结构越稳定。