基于GAT-Informer模型的河南省空气污染物浓度预测

摘要：为了提高空气污染物浓度预测的精度和效率，提出了一种结合图注意力网络（GAT） 和Informer的深度学习模型——GAT-Informer。该模型利用GAT提取各个监测站点之间的空间特征，充分利用相关站点的特征信息；Informer有效地挖掘时间序列的长期信息和局部变化，通过将时间信息和空间信息进行整合，从而预测河南省100个空气质量监测站点六种污染物浓度。研究结果表明，该模型在平均绝对误差（MAE） 、均方根误差（RMSE） 、平均绝对百分比误差（MAPE） 等评价指标上优于长短期记忆网络模型、支持向量机回归模型、历史平均模型以及时空图卷积等模型。

关键词：空气污染物；浓度预测；图注意力网络；深度学习；时间序列

中图分类号：TP18    文献标识码：A

文章编号：1009-3044（2025）07-0006-05

开放科学（资源服务） 标识码（OSID）

0 引言

大气污染因影响人类健康、制约国家发展而成为全球最关注的环境问题之一[1]。随着城市化和工业化的不断加快，许多国家和城市的空气污染日益严重。精确掌握空气质量分布对于保护居民健康和空气污染防控非常重要[2]。

国内外在空气质量预测领域取得了丰硕的研究成果。刘威[3]使用支持向量机模型对某市2013年1月至8月的空气质量指数数据进行实证分析，验证了支持向量机模型在回归预测方面的作用，为空气质量预测提供了一种具有实用价值的方法。史学良和李梁[4]等人为解决线性数据可能产生的过拟合现象，利用改进的长短期记忆网络模型对太原市空气质量指数进行预测。

考虑到空气污染数据固有的时空属性，研究者将空间信息整合到深度学习模型中以提高预测效果，涉及空间建模的典型深度神经网络主要包括卷积神经网络和图神经网络等。Yeo和Choi[5]等人采用五层卷积神经网络和三层门控循环单元对首尔地区25个监测站的PM2.5进行实时预测，所提出的方法改善了PM2.5预测的准确率。Faraji和Nadi[6]等人开发了一种针对德黑兰PM2.5的时空预测模型，该模型将三维卷积神经网络与门控循环单元相结合以实现PM2.5的短期预测。Wang和Li[7]等人提出了一种长期PM2.5预测模型，该模型采用了图神经网络和门控循环单元的组合，提升了模型捕获细粒度和长期影响的能力。廖若雯和黄恒君[8]提出了一种多视角融合思路，通过建立图注意力长短期记忆时空预测模型，从空间和时间角度对西安市2021—2023年PM2.5浓度进行预测。

本文将GAT模型与Informer模型融合构建GAT-Informer模型用于预测河南省空气污染物浓度，GAT对各个站点之间的空间特征进行提取，Informer对各个站点的时间特征进行提取，并将模型与长短期记忆网络模型、支持向量机回归模型、历史平均模型以及时空图卷积模型[9]进行对比，验证了模型的有效性。

1 模型构建

1.1 图注意力网络（GAT）

图注意力网络[10]是一种处理图数据的深度学习网络模型，通过自适应地为邻接节点分配不同的权重来增强节点表示。GAT模型图注意力层的计算主要有以下两个关键步骤：

1） 计算注意力系数。计算空气质量相邻站点与目标站点之间的相似系数[eij]，即表示节点[i]对节点[j]的影响系数因子，通过节点[i]和节点[j]之间的距离[dij]计算得到[W]中的每一个元素[wij]。

[eij=a（[Whi‖Whj]），j∈Ni]       （1）

[αij=Softmax（eij）=exp（LeakyReLU（eij））k∈Niexp（LeakyReLU（eik）） ]    （2）

式中：[Ni]为节点在第[i]个时刻的时间特征，[W]是参数的权重矩阵，通过左乘操作来增加节点特征的维度；LeakyReLU为激活函数，[‖]为将节点特征变换之后的维度进行拼接。新的向量与变换特征维度之后的向量进行内积，然后通过激活函数激活权重，接着对权重进行分配，采用Softmax归一化将每个节点的相似系数结果进行归一化处理。

2） 计算归一化注意力系数对应特征的线性组合。

[h'i=σ（j∈NiαijWhj）]             （3）

式中：[h'i]表示GAT输出新的特征，这个特征融合了自身节点和邻居节点的信息，[σ]为激活函数。

[h'i（K）=Kk=1 ‖σ（j∈NiαkijWkhj） ]     （4）

式中：[αkij]为第[k]组注意力机制计算出的权重系数，[Wk]为对应的输入向量的线性变换矩阵，[h'i（K）]是最终输出的每一个节点的特征向量。

1.2 Informer模型

GAT模型在空气质量监测站点污染物浓度的空间特征提取方面表现优异，但在时间序列的提取能力方面仍有待提升。空气质量数据的时序特征模型需要充分挖掘时序数据之间的关系，因此本文选择Informer[11]作为时序特征模型。

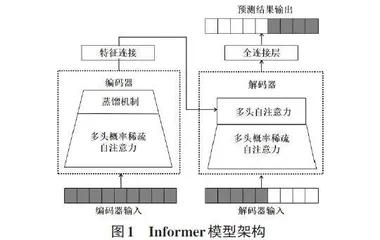
Informer模型是一种新型的基于注意力机制的Transformer[12]模型，旨在解决传统Transformer模型在时间序列预测中遇到的问题，这些问题包括自注意力机制的二次时间复杂度、堆叠层导致的内存瓶颈以及预测速度缓慢等。Informer模型架构如图1所示。

Informer模型的实现步骤原理如下。

1） Informer模型创新性地引入了KL散度作为衡量注意力分布差异性的工具。较高的KL散度值表明注意力分布中某些部分比均匀分布更具信息重要性或显著性，从而允许模型更加聚焦于这些关键信息点。第[i]个查询向量query的稀疏性度量公式为：

[M（qi，K）=lnj=1LKeqikTjd-1LKj=1LKqikTjd]   （5）

式中：第1项是Log-Sum-Exp（LSE），第2项是算术平均值。概率稀疏自注意力计算公式为：

[attention（Q，K，V）=Softmax（QKTd）V]     （6）

式中：[Q]、[K]、[V]分别为查询向量、键向量和值向量组成的矩阵，[d]为防止梯度消失而增加的比例因子，[Softmax]为激活函数。

2） 自注意力蒸馏机制：通过层间蒸馏，每一层都提炼出核心特征，并在下一层中以此为基础构建更加高效和集中的自注意力表示。从第[j]层到第[j+1]层的蒸馏过程计算公式为：

[  Xtj+1=MaxPooling（ELU（Conv1d（[Xtj]att）））]  （7）

式中：[att]表示注意力块，[Conv1d] 表示卷积操作，[ELU]为激活函数，[MaxPooling]为最大池化操作。

3） 生成式解码器架构：生成式解码器采用经典的架构模式，其核心由两个并行、结构相同的多头注意力层构成。解码器的输入向量计算公式为：

[Xtfeed_de=Concat（Xttoken，Xt0）ϵR（Ltoken+Ly）dmodel]  （8）

式中：[Xtfeed_de]为解码器的第[t]个输入序列，[Xttoken]为第[t]个输入序列的起始值，[Xt0]为目标序列的0值占位符。

1.3 GAT-Informer组合预测模型

首先，需要定义GAT-Informer的输入特征。与通常的时间序列预测不同，每个站点的污染物浓度不仅受到前一时刻污染物浓度的影响，还与相邻站点的污染物浓度密切相关。为了充分利用站点之间的空间相关性，将所有站点的污染物历史浓度作为模型的输入，然后利用GAT对空间维度信息进行聚合，并将处理后的目标节点特征传递给Informer。最后，Informer利用GAT传输的目标节点特征，实现对目标节点的浓度预测。其算法步骤如下：

1） 获取描述空气质量中六种污染物浓度的数据（PM2.5、PM10、SO2、CO、NO2、O3） ，对缺失数据进行填补并进行归一化处理。

2） 利用归一化后的数据集进行站点相关性分析，将数据集划分为训练集、测试集和验证集，运用GAT-Informer模型进行训练，并对模型中的超参数进行分析。

3） 将测试集数据带入模型中，最终输出各个站点去归一化后的空气质量污染物浓度数据，模型架构如图2所示。

2 实证分析

2.1 问题描述

假设有[N]个空气质量监测站点，用[V={v1，v2，...，vN}]表示空气质量监测站点的集合，其中每一个站点都包含有小时级别的6种污染物浓度数据。通过设置历史时间窗口[T]，根据历史时间窗口[T]中污染物浓数据预测下一个时间段[t]污染物浓度。本文中每次只预测一个污染物浓度数据，用[X={X1，X2，...，XT}]来表示每个站点的特征矩阵。即该目标是预测第[i]个站点未来[t]个时间段的污染物浓度数值，可以用[yi={yT+1i，yT+2i，...，yT+ti}]来表示。

2.2 实验数据

实验数据来源于中国环境监测总站[13]，选取河南省100个空气质量监测站点的数据，时间范围从2021年1月1日至2023年12月31日，数据为小时级的6种污染物浓度。监测站点的数量如下。郑州市12个；安阳市6个；鹤壁市5个；焦作市7个；开封市6个；洛阳市10个；漯河市6个；南阳市5个；平顶山市5个；濮阳市4个；三门峡市5个；商丘市4个；新乡市7个；信阳市4个；许昌市6个；周口市4个；驻马店市4个。

本文所用环境为Pytorch，采用Adam[14]优化算法对模型进行优化。由于部分站点缺失值比例超过90%，故本文选择河南省缺失比例较少的100个站点的空气污染物浓度进行预测。缺失值部分通过线性填充将其补充完整。训练集、测试集、验证集的比例为7∶1∶2，滑动窗口长度为12，输出数据长度也为12，最大训练次数为50轮，GAT的层数设置为2。将空气污染物浓度进行归一化处理。

[a'i=ai-aminamax-amin]            （9）

式中：[ai]为数据的第[i]个值，[amax]为该数据中的最大值，[amin]为该数据中的最小值。

2.3 评价标准

为了评估所提出模型的性能，本文选取平均绝对误差（MAE） 、平均绝对百分比误差（MAPE） 、均方根误差（RMSE） 三个评价指标对预测结果的有效性与适用性进行对比分析。MAE、RMSE、MAPE越小，模型的预测效果越好。以下是3个评价指标的计算公式。

[MAE=T=1n|Y（T）-Y（T）|n]            （10）

[MAPE=T=1n|（Y（T）-Y（T））/Y（T）|n]     （11）

[RMSE=T=1n[Y（T）-Y（T）]2n]         （12）

式中：[n]表示实验预测的次数，[Y（T）]和[Y（T）]分别表示真实值和预测值。

2.4 实验结果

2.4.1 采样站点污染物浓度预测

本文选取一个抽样站点，将其6种污染物浓度的真实值与预测值的结果进行表示。其中，黑色曲线表示真实值，灰色曲线表示真预测值，横坐标表示时间，纵坐标表示6种污染物浓度。在图3至图8中，可以看到不同污染物浓度的数据是完全不同的，而且各个污染物的趋势也大相径庭。真实值与预测值接近于同一条曲线，表明模型的预测效果良好。因此，本文提出的模型对于站点之间污染物浓度预测是完全可行的。