学科大概念视角下初中数学单元复习结构化教学探索
作者: 栾菊 李婷
学科大概念处于学科中心位置,指向的是学科的基本结构,反映了学科本质.可以说,学科大概念是学科基本知识的“主干道”,是落实学科核心素养的方向标.数学大概念包含数学的核心概念,核心概念反映了数学的本质、主要思想方法、数学技能、解决和研究问题的一般思路、数学观念等.我们在进行单元复习课教学时用大概念加以统领,可以将原本零散的知识汇聚起来成为一个有机整体.这样的单元复习课,有利于知识与方法的迁移,促进学生知识的整体建构,能让学生感受到学习的意义和价值.《义务教育数学课程标准》(2022年版)指出课程内容重点是对内容进行结构化整合,探索发展学生核心素养的路径.学科大概念引领下的初中数学结构化教学是基于数学学科基本知识的相互关联的结构化集合体,是在大概念的引领下将数学知识进行串联,形成体系,通过对学习主题的重构,实现内容的结构化,凸显学科内容的整体性,学科本质的一致性.基于此,笔者以初中数学“分式”单元复习教学为例与各位教育同仁共同探讨如何在学科大概念的引领下落实单元复习课,提升学生能力.
一、例谈单元复习结构化教学的设计与分析
(一)“分式”章节课标要求分析
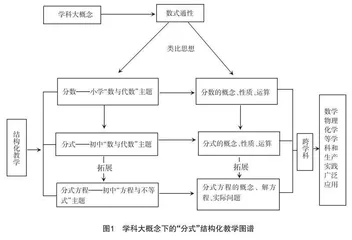
“分式”是人教版数学教材八年级上册第十五章的内容,是初中阶段继“整式”之后的又一个重要的代数基础知识,要类比小学这部分知识的学习路径进行研究.“分式”章节的基本内容是分式的概念及其基本性质、分式的混合运算、分式方程及利用分式方程解决实际问题.学科大概念下的“分式”结构化教学图谱如图1所示.
根据对课标的分析可知,“分式”一章旨在引导学生掌握分式的概念及对最简形式的理解,灵活运用分式性质进行约分、通分,并能熟练地对分式进行加、减、乘、除混合运算.数与式的研究具有数学内容的整体性、逻辑的连贯性、思想的一致性.数是式的具体呈现,式是数的抽象表达.根据对学科大概念下的结构化教学的认识,我们以“数式通性”作为大概念确定目标,以分式的基本性质和四则运算作为教学重点,让学生体会类比、归纳等数学思想方法,提升学生的推理和运算能力,培养核心素养.“分式”章节的教学流程如图2.
(二)“分式”单元复习结构化教学设计与分析
环节1:联系生活,设计题目
1.某药店新购进一批药品,该药品总共花费了x(x+1)元,一共买了x-1盒,则每盒的单价是_________元.
2.甲乙两个工程队共同参与政府的一项修路工程,甲工程队单独施工1个月完成这项修路工程的二分之一,甲工程队的工作效率为_________,乙工程队单独施工x个月完成这项修路工程,乙工程队的工作效率为_________.
3.小轿车每分钟行驶1千米,x+1分钟小轿车行驶了_________千米.
4.一个长方形的面积是x2-1平方米,其长为1-x米,则长方形的宽为_________米.
5.圆的周长为2 cm,则圆的直径为_________cm.
教学说明:分式单元应用题主要包括行程问题、工程问题、利润问题、图形问题.教师在问题情境创设环节引入核心知识点的基础知识,为后面利用分式方程解决实际问题埋下伏笔.
环节2:问题探究,复习旧知
问题1 上述实际情境中所得的式子哪些是分式?哪些是整式?
问题2 上述分式都是最简分式吗?
问题3 上述分式有意义的条件是什么?
问题4 上述分式值为0的条件是什么?
问题5 以小组为单位将上述实际情境中所得的式子任选两个设计一个分式乘除运算或加减运算的题目.
问题6 将问题5中的乘除运算加(减)一个式子、将加减运算乘(除以)一个式子,设计出一个混合运算的题目.
问题7 将问题6中混合运算增加“求值”要求,选择一个你喜欢的数代入求值.
教学说明:基于情境中的6个式子,以问题串驱动教学,教师由浅入深地复习分式的定义、最简分式、分式有意义的条件、值为0的条件.以开放式设计题目的教学活动,复习分式的概念及运算,不仅增强了学生的求知欲,还有利于发散学生的思维,让学生在反思中提炼知识与方法.在计算环节增加“求值”的过程,将运算与分式有意义的条件结合起来,体现知识的整体性与综合性,有利于构建高阶思维.
环节3:回归生活、应用生活
教师解析环节1系列问题并引导学生迁移解决以下实际问题:
1.某药店新购进一批药品,该药品总共花费了x(x+1)元,一共买了x-1盒,则每盒的单价是x(x+1)/x-1元.
销售问题:为了建设美丽的校园环境,某市一中学在今年年初购买了甲、乙两种花苗在学校的四周进行栽种.已知甲种花苗的单价比乙种花苗的单价多10元,用600元购买甲种花苗的棵数恰好与用450元购买乙种花苗的棵数相同.若设甲种花苗的单价为x元,则可列方程为_________.
2.甲乙两个工程队共同参与政府的一项修路工程,甲工程队单独施工1个月完成这项修路工程的二分之一,甲工程队的工作效率为1/2,乙工程队单独施工x个月完成这项修路工程,乙工程队工作效率为1/x.
工程问题:甲乙两个工程队共同参与政府的一项修路工程,甲工程队单独施工1个月完成这项修路工程的二分之一,乙工程队单独施工x个月完成这项修路工程.现在先由甲工程队单独施工1个月完成这项修路工程的二分之一,这时增加了乙工程队,两工程队又共同工作了半个月,这项修路工程全部完成.求乙工程队单独施工要几个月完成,可列方程为_________.
3.小轿车每分钟行驶1千米,x+1分钟行驶了x+1千米.
行程问题:徐曼、李想两名同学分别从距离活动地点800米和400米的两地同时出发参加“童心读书会”的分享活动.徐曼同学的速度是李想同学的速度的1.2倍,李想同学比徐曼同学提前4分钟到达活动地点.求李想同学的速度,若设李想同学的速度是x米/分,可列方程为_________.
教学说明:教师在分式方程的应用环节呼应环节1问题情境,利用问题情境中的素材启发学生深入思考,利用分式方程这一模型解决销售问题、工程问题、行程问题.在课程中,教师让学生回归生活中去应用知识,在复习分式方程的内容时,利用表格作为辅助来分析已知、未知量,抓住数量关系、等量关系,设未知数列方程,让学生能够用数学的语言表达现实世界,培养学生的数学核心素养.虽然本环节设计的三个情境各不相同,但是在类比迁移中,学生可以体会到总量与分量的关系决定了方程是整式方程还是分式方程.
环节4:反思回顾,形成体系
此环节,教师以小组汇报的形式进行本节课的小结,如图3所示回顾复习历程,学生在独立思考的基础上,在互帮互助的氛围中自主建构单元知识体系.
二、关于学科大概念视角下初中数学单元复习结构化教学的思考
1.初中数学单元复习结构化教学策略
在进行初中数学单元复习结构化教学时,首先,教师得明确单元目标,将整个单元的内容分解为若干个相互关联、层层递进的小节,确保每节课既有独立性又能构成完整的知识体系.课程设计遵循“由总到分,再由分到总”的原则,帮助学生逐步理解和掌握数学概念.其次,教师要注重运用“问题引导-探究发现-总结归纳”的教学模式,形成结构紧密的问题链驱动任务的完成,鼓励学生主动思考、合作探究,激发学生的求知欲;通过小组讨论、实验操作等方式,让学生亲身体验知识的发现过程。最后,教师再引导学生总结归纳所学内容,形成自己的知识体系.
2.学科大概念如何引领结构化教学
学科大概念是数学教学的灵魂,它贯穿于整个单元乃至整个学科的教学之中,为结构化教学提供了明确的导向.只有准确把握学科大概念,才能有效地引领结构化教学.具体来说,首先,教师要深入分析初中数学的核心大概念,如函数思想、几何变换、类比迁移等,并将这些大概念作为教学的出发点和归宿.然后,在设计单元复习课时,教师再围绕这些大概念来组织教学内容和选择教学方法,确保教学内容与学科大概念紧密相连,形成完整的知识链条.
3.学科大概念引领下初中数学单元复习结构化教学的实施效果
学科大概念是数学核心与本质的体现,能有机联结各知识点.在单元复习中,结构化教学可以围绕大概念,系统整合零散知识,帮助学生构建完整的知识网络,深化数学理解.此教学方式重视数学思维培养,如逻辑推理、抽象概括等,通过设计具有挑战性的问题,引导学生分析解决,既激发兴趣,又发散思维.同时,教师强调以学生为中心,通过小组合作、项目学习等方式,培养学生自主学习与合作探究能力,助力学生形成良好学习习惯,提升综合素养.结构化教学使学生在大概念的引领下,系统地掌握数学知识,提高思维能力,为未来发展奠定坚实基础,并全面提升包括语言表达、团队协作、创新思维等在内的综合能力.
【本文系云南省教育科学规划项目“小初高数学贯通式育人路径研究”(课题编号:BC23086)的阶段性成果】