高等院校研究生招生调剂治理：竞争、模式与策略

摘 要：研究生教育是高等教育的高级层次，提高生源质量是落实高校“双一流”建设战略规划的有效途径。其中研究生调剂作为招生工作的一种重要补充形式，越来越多地受到国家、教育管理部门以及高等院校的关注和重视。基于水平差异竞争视角，构建Spokes差异竞争模型，分析不同声誉高校的招生调剂策略，探讨新冠疫情期间研究生网络远程复试模式对招生调剂的影响。研究结果表明：1）调剂系统中竞争高校数量的不同使学校收益呈现出显著差异;2）不同声誉高校在生源竞争中收益也存在很大差异，声誉越低的高校在竞争中处于越不利的位置;3）在相同外部环境条件下，调剂考生的网络远程复试模式优于线下复试模式;4）在相同的复试模式下，线下复试对声誉高的院校更有利。

关键词：研究生教育;招生治理;竞争;网络远程复试模式

一、引言

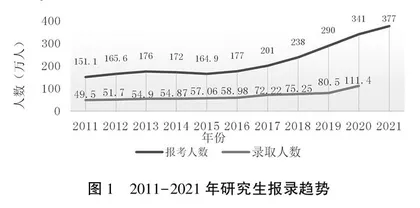
研究生教育是高等教育整体的重要组成，其培养质量对科教兴国战略、人才强国战略的实施以及创新型国家的建设具有重要的战略意义。作为学位与研究生教育的生命线，研究生招生成为高等教育的重要环节，提高生源质量对于高校“双一流”建设意义重大。近年来，硕士研究生的总体招生规模与报考人数大体上呈快速增长态势。2018年硕士研究生报考人数为238万，2021年硕士研究生报考人数为377万，比2018年增加139万，增长比例接近70%。

现阶段我国高校硕士研究生招生方式主要包括推免生、第一志愿考生和调剂生三种。中国教育在线调查数据（43万人次）显示，考生在选择院校时，报考地区多集中在名校资源丰富，经济发展水平较高的地区，且在研究生计划报考前10的院校中，70%的院校为“985”高校。由于招生计划与考生报考志愿的严重不平衡，有相当一部分考生无缘第一志愿，此时他们就需要调剂达到继续升学的愿望，而第一生源不足的高等院校也需要通过调剂完成招生计划。另一方面，第一志愿无约束力、考生可以任意调剂的乱象，造成招生单位成本大增、暗箱操作，存在招生目标达不到的风险。调剂成为高校研究生招生工作的重要组成部分，调剂现象几乎影响所有的招生单位和近1/3的考生[1]。在硕士研究生调剂过程中，出现一系列亟待解决的问题，例如调剂考生志愿过于集中，部分高分考生落榜最终无缘高校[2][3];调剂高校的调剂系统开放时间不合理，导致招生质量差效率低，不得不进行二次、三次调剂，甚至四、五次调剂，浪费大量的人力、财力和物力;调剂考生的失信问题，功利心强，在调剂过程中临时变卦，导致许多无效调剂，增大招生单位的招生成本，使得招生单位之间竞争加剧，内卷现象严重，整体社会福利下降，成本增大。2020年突如其来的新冠疫情，使得硕士研究生招生复试工作由线下转为线上。网络远程复试模式成为各高校在疫情期间首选的研究生复试方式，打破了高校原有的招生节奏和方式，同时也给各招生单位带来前所未有的机遇与挑战。

因此，本文通过对研究生调剂事件进行大量的调查分析，围绕高校“双一流”建设中心工作，运用多企业水平差异竞争模型，构建三阶段动态博弈模型，探讨高等教育研究领域的研究生招生治理问题。通过引入学生被首选学校录取和被备选学校录取获得效用的差异性这一假设，重点研究三个问题：1）不同声誉的学校如何优化招生策略竞争获取更多的优质生源;2）学生如何策略性地选择心仪的学校;3）疫情期间的网络远程复试模式是否影响高校的招生策略以及考生的录取成功率。

二、文献回顾

与本文研究密切相关的研究方向有两个：

第一个研究方向是：高校生源竞争。生源质量是人才培养体系的基础，招收优质生源已成为高校间竞争的重要领域之一。随着我国高校大学生招生规模的扩张，港澳台地区及国外高校、国内民办高校的加入，我国高校在研究生招生上的生源竞争愈发激烈[4]。早在1981年，美国学者David Chapman针对高校间激烈的生源竞争，从营销学的角度构建一个影响大学生报考高校的选择行为模式，认为考生的择校行为是考生的个性差异与外部影响因素共同作用的结果，最终考生偏好于某一高校，从而做出自己的大学选择[5]。中国学者吴剑峰从高校生源竞争的根源入手，分析高校生源竞争激烈的原因并提出规范竞争的建议[6]。高校竞争力受综合竞争力、区域位置、高校知名度与声誉等因素的影响，马辉通过分析高校核心竞争力的概念，提出以提升核心竞争力为主线的高校基本发展思路[7]。任初明从量与质两个维度，采用报录比和录取平均分两个指标对高校生源竞争力进行测量，得出这两个指标与生源竞争力成正比[8]。建立生源竞争力测量方法，测量某高校的生源整体竞争力，也可测量某一学科或专业的生源竞争力。黄静等将研究生招生质量解构为三种：结构质量、生源质量和选拔质量，并基于以上三方面分析我国现有研究生招生质量保障体系的不足之处[9]。唐检云通过对研究生报考志愿选择影响因素进行调研，了解影响考生选择志愿的真实因素，分析一般院校如何吸引优秀生源[10]。在高等院校招生规模不断扩大、各院校之间招生竞争日趋激烈的条件下，杨正理等利用海量招生异构数据，结合云计算技术，利用Mapreduce并行计算模型和Spark框架对高校历史数据进行分析，提出一种基于Hadoop的分布式并行随机森林算法模型，利用此算法模型处理高校招生大数据，实现对高校未来招生策略的预测[11]。梳理高校生源竞争相关文献可以发现，现有研究多侧重于从理论层面研究高校生源竞争的影响因素，分析高校的招生策略，较少通过数学模型分析在生源竞争中，高校如何确定招生策略来吸引更优质的生源。2020年的新冠肺炎疫情打破人们原有的生活节奏和生活方式，同时也给各高校研究生复试带来前所未有的挑战，各高校在短时间内从“线下复试”全面切换成“线上复试”，网络远程复试成为各高校在疫情期间首选的研究生复试方式[12]。疫情的发生对高校招生的影响也值得进一步探讨，为我国今后顺利高效地开展网络远程复试提供借鉴作用。合理而针对性的招生策略，有助于高校吸引生源，在生源数量充足的基础上，择优录取考生，提高生源质量，为提高硕士研究生的整体培养质量打下坚实的基础。

第二个研究方向：多企业水平差异竞争模型。水平差异竞争的研究最早来源于Hotelling经典空间竞争模型[13][14]，即线性（直线段）市场上的双寡头厂商定位模型，其后用来较好地解释“伯川德悖论”。后来的众多研究文献都是基于经典Hotelling模型拓展的衍生模型。1）由于Hotelling模型受限于双寡头竞争企业，Salop将线性市场扩展到圆形市场，建立环形Hotelling模型[15]。此模型消除企业数量限制且企业不再拥有各自腹地，更加符合现代竞争情形。后来，许多中国学者也在此基础上，在水平差异化产品市场中用Salop圆周模型分析厂商的定价行为及相互之间产品的差异化程度[16]。2）Von Ungern-sternber基于相同的“地理”假设，构建金字塔模型[17]。此模型允许多公司竞争，把生产者定位在多维金字塔的拐角，把消费者定位在金字塔的线段上，分析具有不同生产成本的企业的利润最大化均衡解。3）Chen&Riordan将Hotelling的双寡头线性城市模型扩展为具有非本地价格竞争和任意数量的差异化企业的全局竞争模型，建立Spokes模型[18]。在Spokes模型中，当新企业进入市场时，仍保持企业之间的对称性，不需要重新定位现有企业在偏好空间中的位置，每个企业都直接与所有其他企业竞争，并引入消费者偏好排序，即根据消费者的偏好将企业依次排序，且赋予不同的权重，有效解决多个寡头参与竞争的问题。4）Motta&Kind通过产品差异度s这个变量描绘消费者效用函数，构建一个代表性消费者偏好模型[19][20]，分析竞争力如何影响媒体公司提高收入的方式，允许市场上竞争对手数量的增加，得出竞争会导致更高的产出，消费者偏好模型（representative consumer’s preference model）可以视为对建立在Hotelling模型和Salop模型框架上差异化竞争研究的补充。

本文选择Spokes模型，主要有以下几方面的原因：1）学生可以根据学校的声誉对调剂系统中的可调剂学校进行排序;2）模型要刻画出声誉不同的学校彼此的相互竞争关系;3）模型要便于体现学生被声誉不同的学校录取的效用差异;4）尽可能简化模型的分析。

三、模型构建

一般性地，考虑社会系统中有i=1，2，...，N所互相竞争的可调剂学校，每个学校拥有数量有限的调剂名额，且仅通过调剂系统来完成学校的招生工作;学生会根据个人偏好来选择学校。在调剂系统中，假设学生有两种学校可以选择：一是首选学校;二是备选学校。同时招生单位复试模式有两种可以选择：一是线上复试模式;二是线下复试模式。

本文运用Spokes模型刻画学生偏好和多个学校竞争的市场环境[21][22]，每个学校用一条长度1/2的线段的原点来表示，并称这条线的另一端为它的终点。对于每一所学校i，与之相关的线段用li来表示，所有li的终点交汇于一点，称之为中心，这就形成一个拥有同一个中心的放射性网络，这个网络代表偏好空间。假设学生总量为1，并且均匀地分布在Spokes网络的每条线段上。位于（li，xi）的学生通常根据效用最大化原则来选择学校，学校i为首选学校，剩余N-1个学校以均等的概率1/（N-1）成为备选学校，到任意备选学校j（j≠i）的距离为（1-xi）。

每个学生都是独立的个体，可以被不同声誉的任一学校录取。针对社会系统中所有的学生，采用效用函数U（xi）表示学生被录取的效用。准确来说，效用代表学生根据被录取学校的声誉所获得的满意程度，具体效用函数如下所示：

U（xi）=ui-cxi，首选学校录取的效用uj-c1-xi，备选学校录取的效用

假设每位学生首选离他最近的学校，其余N-1所学校对学生来说是无差异的，最终选择哪一所学校，由各个学校为学生带来的效用决定。任意学校i对于学生来说，

ui=βivi-1N-1∑j=1，2，…，Nj≠iγvj;uj=θui（1）

对于任意学校而言，在声誉博弈中，自身声誉带来的影响大于其他学校声誉带来的影响[23]，即i，βi>γ。θ表示学生对备选学校的感知差异程度[24]，θ越大意味着学生对备选学校的感知越接近首选学校，首选学校和备选学校对于学生来说差别越小，c为学生被学校录取所付出的单位成本。

此时，如果满足等式ui-cxi=uj-c（1-xi），则学生（li，xi）选择学校i和学校j获得的效用是相等的。因此，xi=（ui-uj）/2c+1/2。由此可知，如果ui=uj ，则xi=1/2 ，恰好位于“星状网络”的中心;如果ui-uj>0，则随着（ui-uj）的增大，xi点向学校i靠近。也就是说，学生对学校i的需求增大，而对学校j的需求减少。对于被两个学校i和j录取毫无差别的学生来说，其被录取的效用最小，其距离两学校的距离最远，即当ui-c*（（ui-uj）/2c+1/2）>0时，学校i和学校j的招生市场被完全覆盖。

为了直观上更清楚本文的相关参数和变量符号，先用表1进行归纳说明。

假设社会系统上有NN2所学校，分别位于半径为1/2的Spokes模型的N个端点上，第i所学校所在的线段记为li。若满足ui-c*（（ui-uj）/2c+1/2）>0 ，则整个Spokes网络将会被学生完全覆盖。这样，学生对学校i的需求可以达到qi，则

qi=2N（N-1）∑j=1，2，...，Nj≠iui-uj2c+12，i=1，2，......，N（2）

根据以为文献假定录取的学生分数与学校i声誉的函数是线性关系[25]，即：

vi=αsi（3）

其中，α为学校的声誉和学生分数的比例系数。

因此，学校i的收益函数如下：

πi=siqi（4）