基于支架式教学的“圆的面积”教学设计研究

摘 要 “圆的面积”是小学数学学习的重点，但是学生在学习过程中存在诸多认知困难。根据支架式学习理论进行教学设计，基于化曲为直和极限思想进行圆的面积公式的建构，为小学一线数学教师的教学提供可借鉴的方法和策略。

关键词 小学数学 支架式教学 圆的面积 教学设计

一、引言

“圆的面积”是小学阶段学生接触的第一个曲线图形的面积的计算，是平面图形测量中由直线图形向曲线图形过渡的关键点。[1]圆的面积公式的探索方法为后续圆柱体体积公式的探索以及无理数的学习做了铺垫，其推导过程中蕴含着数学推理意识以及化曲为直和极限等数学思想。因此，“圆的面积”在小学数学中占有重要地位。然而，学生在“圆的面积”的建构过程中存在诸多认知困难，例如，在将圆的面积转化成已学过的平面图形的面积过程中，学生对于为何要将圆的面积平均分、怎么平均分，以及能够拼成哪些图形存在理解困难；[2]另外，学生在将圆无限分割成多个小扇形的过程中蕴含的化曲为直和极限思想的理解存在困难。本研究基于支架式教学理论，基于学生在“圆的面积”学习过程中存在的认知困难，对“圆的面积”进行教学设计，将为小学一线数学教师的教学提供可借鉴的方法和策略。

支架式教学是指在学习过程中，教师为学生提供相应的外部支持，帮助学生跨过“最近发展区”，达到潜在的学习发展水平。随着学习的不断深入，教师应当撤掉学习上的“支架”，让学生成为学习和探究的主体。[3]支架包括教师示范、出声思维、提出问题、改变教材、书面或口头的提示或者暗示。[4]支架在教学中通常表现为举例、问题链、提示、图表、教具及多媒体演示等形式。支架式教学理论认为，教师通常先将学生引入一定的问题情境中，并提出所要解决的问题，教师搭建各种类型支架，为学生的新知探索和学习提供帮助并引领探索方向，最后师生总结提升。

二、“圆的面积”教学目标设计

1.在探索实际问题情境中，了解“圆的面积”的含义。

2.在推导圆的面积公式的过程中，体会化曲为直和极限思想，发展推理意识。

3.在应用“圆的面积”公式解决问题过程中，能正确计算圆的面积，发展模型意识、数学运算、应用意识。

三、“圆的面积”教学过程设计

（一）环节一：创设情境

【数学史情境】“圆的面积”的求解历史

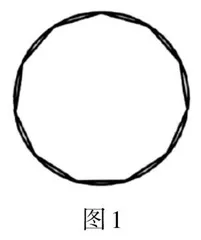
刘徽是我国魏晋时期的数学家，他在《九章算术》方田章“圆田术”的注中提出把“割圆术”作为计算圆的周长、面积以及圆周率的基础。“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”刘徽从圆内接正六边形开始，将边数逐次加倍，得到的圆内接正多边形就逐步逼近圆，如图1所示。

设计意图：引入数学史，介绍相关的历史背景，激发学生的学习兴趣和求知欲，使学生了解知识的发生、发展过程，从而促进学生更深入地体会极限思想。

【应用情境】学校打算新建一个半径为15 m的圆形草坪，圆形草坪的占地面积为多少平方米？

师生活动：学生阅读题目，思考圆形草坪的面积的求法。

设计意图：教师创设真实的问题情境，激发学生的求知欲，并提出要解决的问题。

（二）环节二：新知探究

1.搭建研究思路和方法支架

问题1：我们学习过哪些平面图形的面积？这些平面图形的面积的计算公式是如何得来的？

学习活动：学生独立思考之后回答教师的问题，教师引导学生提炼化归的思想方法。

设计意图：沟通新旧知识之间的联系，激活学生已有的关于平面直线图形的面积的计算思路和方法，搭建支架，促成迁移，进而帮助学生在自己经验范围内找到研究平面曲线图形的面积的计算方法。

2.搭建问题支架，引领思维发展

问题2：这些平面图形的面积是通过数格子或者分割后拼成已学图形的面积获得的，你能用类似的方法求圆的面积吗？

学习活动：借助教师提供的若干圆，学生动手实践，自主探究（教师巡视指导，先挑选几份数方格法的作品）。

预期学生作品展示，如图2所示，并让学生汇报思路。

问题3：他们是用什么方法求解的？你认为上面哪个方法的计算会更接近圆的面积？为什么？这种数方格的方法求圆的面积有什么不足？

学习活动：学生通过独立思考，回答问题。

【师】利用数方格的方法，可以把一个个面积单位累加起来计算圆的面积，方格分得越小，估计值就会越接近圆的面积。

问题4：圆的面积除了平均分成小方格，还可以平均分成什么图形？分割后的图形能拼成什么图形？（大部分学生能够想到平均分成小扇形，如果想不到，提示学生对折圆形纸片。大部分学生拼成近似的平行四边形或者长方形，如果想不到拼成梯形和三角形，教师可提示学生是否还有其他拼法。）

预期学生作品展示，如图3所示，并让学生汇报思路。

追问：你是如何想到平均分成小扇形的？和平均分成小方格相比，哪种方法容易操作、更精确一些？（学生存在困惑，教师提示长方形借助长和宽均分成小方格，圆形借助圆心和半径均分成小扇形。）

针对第一种拼法，教师选取将圆8等分和16等分拼成的图形进行展示，如图4所示，引导学生观察。

问题5：观察图4中的图形，你们有什么发现？

教师利用课件演示将圆平均分成32等份以及64等份后再拼起来。

问题6：再继续等分下去，分成128等份后拼成的图形会有什么变化？分成256等份呢？如果一直无限分下去，等分成无数份，会拼出什么图形？

学习活动：学生观看教师的多媒体演示，回答教师提出的问题。

【师】这些方法的共同之处是都将圆平均分成若干个小扇形，之后拼成前面已经学习过的平面直线图形。

设计意图：首先，教师以学生容易想到的数方格法入手探索圆的面积，通过方格细化法会更接近圆的面积渗透极限思想，并引导学生体会方格越小数起来越麻烦，且结果不够精确，为圆平均分成小扇形做铺垫。其次，在将小扇形拼成已知直线图形的过程中，教师通过提问学生和多媒体演示支架引领学生转化成多种图形，渗透化曲为直和极限思想。

3.图示支架归纳出圆面积公式

学习活动：教师引导学生找到拼成后的平行四边形（长方形）的底（长）和高（宽）与圆的周长和半径之间的关系，并推导出圆的面积公式。圆的面积公式的推导如图5所示。

问题7：如果把圆转化成三角形和梯形，以16等分为例，你能试着用它们来推导圆的面积的计算公式吗？这些方法之间有什么共同之处？

学习活动：学生迁移平行四边形推导圆的面积的思路，计算三角形和梯形的面积，得出圆的面积公式为[πr2]，最后教师总结。

【师】圆的面积是未知的，我们将其转化成已知图形，进而探索出圆的面积公式，应用了化曲为直的方法，分割份数越多越接近圆的面积。

设计意图：教师引导学生利用多种转化图形得到相关数据，通过图示支架推导出圆的面积的计算公式，发展归纳推理意识，体会化曲为直和极限等数学思想。

（三）环节三：实践应用

练习1.学校打算新建一个半径为15 m的圆形草坪，圆形草坪的占地面积为多少平方米？

练习2.一个圆形的周长是31.4米，这个圆形的面积是多少平方米？

学习活动：倾听教师示范讲解练习1，学生做练习2。

设计意图：练习1是利用圆的面积公式直接解决“环节一”中提出的问题，实现首尾呼应。练习2是已知周长求面积，是练习1的变式，进一步促进学生对于圆的面积公式的理解和应用。

（四）环节四：总结提升

教师评价学生的学习表现，并提出问题：

1.本节课你学到了哪些知识和技能？

2.圆的面积公式是如何推导的？

3.你还有什么困惑吗？

4.圆的面积计算公式还有其他推导方法吗？（提示：除了平均分成小扇形之外，圆还能分成哪些图形？可以分成圆环吗？分成的圆环能拼成什么图形？除了平均分成偶数个小扇形，圆是否也可以平均分成奇数个小扇形？）

设计意图：结合学生的回答，教师带领学生梳理圆的面积计算公式的推导过程以及所涉及的数学思想方法，并让学生探索圆的面积公式的其他推导方法，将封闭的课堂变成一个开放的课堂，进一步发展学生数学思维的发散性和深刻性。

四、“圆的面积”教学设计反思

（一）搭建支架促进学生“现有水平”向“潜在发展水平”的转化[2]

本教学设计中，深入分析了学生“现有水平”向“潜在发展水平”转化过程中存在的认知困难。以此为出发点，以学过的平面直线图形的面积公式的研究方法为支架，以分析数方格法的局限性为切入点，逐步通过问题、教具、多媒体演示以及图示支架引导学生的数学探究。在实际教学中，教师搭建的支架应具有梯度，但是梯度要适度，确保学生在最近发展区中开展数学探究。

（二）问题链作为支架引领学生的数学探究活动

教师在数学探究活动开展的过程中设计层层深入的问题链支架引领学生思考。例如，我们学习过哪些平面图形的面积？这些平面图形的面积的计算公式是如何探索的？圆的面积除了平均分成小方格，还可以平均分成什么图形？分割后的图形能拼成什么图形？这些环环相扣的问题循循善诱地引领学生回顾旧知并建立联系、方法迁移探究新知、比较概括提炼思想，促进学生数学核心素养的发展。

为了实现教学效果最优化，教师应该深入地分析学生数学学习存在的认知困难，基于学生认知困难搭建多样化的学习支架，辅助学生的数学探究，进而促进学生自主学习能力的发展。

[参 考 文 献]

[1]肖慧，虞秀云.以学定教，顺学而导：基于学生学习路径分析的圆的面积教学设计[J].数学教学通讯，2021（4）：11-12+40.

[2]童永健.支架式教学理论在数学课堂中的应用：以沪教版“作为判别式的二阶行列式”教学设计为例[J].中学数学研究（华南师范大学版），2015（11）：4-6.

[3]邱锺慧，马德宜，柳福祥.基于数学史视角的圆面积教学设计思考[J].教学与管理，2019（8）：50-52.

[4]陈琦，刘儒德.当代教育心理学[M].北京：北京师范大学出版社，2007：200-201.

（责任编辑：姜显光）

作者简介：陈丽敏（1976— ），女，辽宁大石桥人，沈阳师范大学教师教育学院副教授，博士，研究方向：数学课程与教学理论研究；王瑾（1975— ），女，辽宁铁岭人，沈阳师范大学教师教育学院讲师，博士，研究方向：数学课程与教学理论研究。

基金项目：本文系辽宁省教育科学“十四五”规划2021年度课题“乡村数学教师网络学习共同体建设的实践研究”（课题编号：JG21EB288）、辽宁省教育厅2021年度科学研究经费项目“学习共同体视域下辽宁省中学名师工作室的建设研究”（课题编号：LJKR0360）的阶段性研究成果。