算法与算理相结合提升问题解决能力

摘要 问题解决能力是一个学生具有数学核心素养的重要体现。通过经历解决真实情境中真实问题的过程，明晰研究对象和问题，小组合作探究不同的问题解决方法，归纳概括并理解算理的一致性，优化、选择问题解决的最优策略，感悟数学知识的应用价值。

关键词 小数乘法 运算方法 算理 问题解决

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）指出，运算能力主要是指根据法则和运算律进行正确运算的能力。[1]8运算能力的培养，首先是明晰运算的对象和意义，并能理解运算的问题；其次是理解算法与算理之间的关系，选择合理简洁的运算策略解决问题，发展学生的推理意识。本节内容选自北京师范大学出版社《义务教育教科书·数学》（四年级·下册）第三单元中“小数乘法”[2]，该单元内容是新课标中“数与代数”领域课程内容的重要组成部分。小数乘法以整数乘法为基础，其运算方法、运算意义是一致的。本研究旨在通过真实问题解决，深化对小数乘法算理的理解和认识，进一步巩固小数乘法的运算方法，核心内容是探究不同运算方法与算理之间的关系，从而能优化、选择运算策略，感受数学知识的应用价值。

一、教学目标设计

1.通过明晰真实情境中的运算对象和问题，探究解决问题的方法，经历从已知走向未知的过程，初步具备多种方法解决真实问题的能力。

2.通过对算法的观察分析，理解不同算法的算理的一致性，初步理解算法与算理的关系。

3.通过明晰算理，优化、选择问题解决的最优策略，感受数学知识的应用价值。

二、教学过程设计

（一）创设情境，明晰对象和问题

【情境】某县正在创建全国文明城市，增加居民的活动空间，提升居民生活的幸福指数，预建设若干个健身广场。展示其中一个健身广场的平面设计图。广场的长、宽分别为30米、20米，计划在广场中修建4个花坛，每个花坛的长、宽分别为3米、2米，花坛以外的部分铺设长、宽分别为0.3米、0.2米的地砖。

问题1：广场、花坛的占地面积分别是多少？需要多少块地砖？

设计意图：通过创设真实情境，激发学生的数学学习兴趣，培养学生观察、提取数学信息的能力，明确情境中的研究对象分别是广场、花坛和地砖。通过问题驱动，明确所要解决的数学问题是地砖的数量。根据题目中数字信息，为学习小数乘法做铺垫。

（二）小组合作，探究算法

[师]地砖铺在广场上除花坛以外的空白区域。因此，要想知道地砖的数量，需要知道花坛以外空白区域的面积。根据前面所学习的长方形的面积公式，回答下列问题。

问题2：广场和花坛的面积分别是多少？铺砖区域的面积是多少？

[生]广场的面积为：30×20=600（平方米）；花坛的面积为：4×3×2=24（平方米）；铺砖区域的面积为：600－24=576（平方米）。

问题3：已知铺砖区域的面积，如果施工单位要计算需要地砖的数量，还需要知道什么？

[生]还需要知道每一块地砖的面积。

追问：地砖的长、宽分别为0.3米、0.2米，那么一块地砖的面积如何计算？

学习活动：以小组为单位，自主探究地砖数量或地砖面积的计算方法。

【学生展示探究结果】

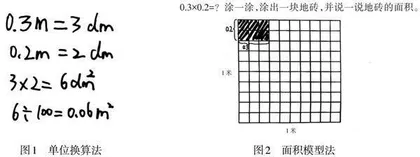
方法一：单位换算法，如图1所示。首先将单位米转换为分米，再进行面积计算，0.3米=3分米，0.2米=2分米，3×2=6（平方分米）；然后根据平方米与平方分米之间的进率是100，将面积单位由平方分米转化为平方米，6÷100=0.06（平方米），所以6平方分米=0.06平方米。

方法二：面积模型法，如图2所示。将边长为1米的正方形的边长进行10等分，得到100个边长为0.1米的小正方形。因此，0.3米就是三个小正方形的边长，0.2米就是2个小正方形的边长。通过画图得到6个小正方形，1个小正方形的面积是0.01平方米，6个小正方形面积就是0.06平方米。

设计意图：通过问题1、问题2及追问的持续驱动，引导学生从题目的已知条件逐渐向待计算结果过渡，最终引出本节课的重点内容——“小数乘以小数”的计算。学生以小组为单位，根据已学知识探究地砖面积的计算方法，经历将未知转化为已知的过程，体会知识间的联系，进一步掌握算法，领悟“转化”思想。

（三）归纳概括，理解算理

问题4：观察上面两种计算方法，它们之间有什么共性？

学习活动：小组讨论交流，归纳出两种计算方法的相同点。

[生]两种计算方法都是将未知转化成了已知的计算，即将“小数乘以小数”转化为“整数乘以整数”，0.3×0.2转化为3×2。

追问1：在两种算法中，6分别表示什么？

[生]在方法一中是6平方分米，6÷100=0.06，6平方分米=0.06平方米；在方法二中是6个小正方形，就是6个0.01，是0.06平方米。

追问2：通过两种计算方法计算后，得到的新单位分别是什么？

[生]在方法一中，1分米乘以1分米等于1平方分米，1平方分米÷100=0.01平方米；在方法二中，0.01是1个正方形面积，作为新单位。

追问3：“÷100”和“×0.01”是一样的意思吗？

[生]“÷100”和“×0.01”都表示把1平均分成100份，其中的一份是一百分之一。虽然它们的表达形式不一样，但是意思是一样的。

设计意图：通过归纳概括两种计算方法的相同点，寻找不同方法间的联系，明确小数乘法可能产生新的计数单位[3]，引导学生深度学习，理解不同方法背后的道理。体会小数乘法转化为整数乘法计算的合理性，实现算理上的一致[4]。感悟运算的一致性，为进一步探索小数乘以小数的计算方法积累经验，促进学生运算能力的进阶发展。

（四）明晰算理，选择最优运算策略

问题5：在理解算理时，两种计算方法均是将“小数乘以小数”转化为“整数乘以整数”。那么，转化为整数后，小数的位数如何在积中体现出来呢？

学习活动：计算0.3×0.2，0.4×0.13，0.13×0.22，学生计算后展示交流自己的想法。

[生]0.3×0.2=0.06，0.4×0.13=0.052，0.13×0.22=0.0286，通过积的小数位数和乘数小数位数比较后，可以发现，积的小数位数等于乘数的小数位数之和。

追问：分析上述两种算法和算理，如何确定小数位数？

[生]先把小数转化成整数，然后根据乘数的小数位数确定积的小数位数。

设计意图：通过运用规律自主计算相似题目，在进一步观察、交流中明晰积的小数位数与乘数的小数位数之间的关系，总结归纳小数乘以小数的计算方法，最终形成通法，由一个问题的解决走向一类问题的解决，培养学生的运算能力不断进阶。

（五）解决真实问题，感受知识价值

问题6：请你帮助施工队计算一下，理论上需要多少块地砖？（写出算式即可）

[生]根据除法法则，地砖数量=铺砖区域面积÷每块地砖面积=576÷0.06。

设计意图：通过计算所需要地砖的数量，与情境问题前后相呼应，解决学生心中的疑虑，体会数学知识在解决真实问题中的重要价值，初步形成规范思考问题的品质，养成一丝不苟、严谨求实的科学精神。由于该计算式涉及小数除法问题，所以学生能写出计算式即可，由教师直接给出答案。

三、教学反思

（一）创设生活情境，唤醒学生问题意识

新课标倡导要注重学生在真实情境中解决问题，让学生感受数学的应用价值。教学初始，教师创设贴近生活实际、真实的“文明城市创建”情境，激发学生探究问题的欲望，让学生明确研究对象和意义，理解所要研究的问题。

（二）通过小组合作，发展学生解决问题能力

小组合作进行交流讨论是学生间进行思维碰撞的重要学习活动形式。文中在环节二、环节三、环节四均采用了小组合作形式。环节二中通过小组合作碰撞出了两种小数乘法的计算方法，环节三在环节二的基础上进行深入研究，理解算理，环节四进一步通过实例分析比较，选择最优的计算策略，促进了学生对小数乘法算理的理解和认识。

（三）通过真实问题解决，促进数学素养发展

与现实生产生活相关联，并能解决真实情境中的真实问题，这是数学知识存在价值的重要体现。运算一致性是指运算之间是有一致或相通的联系。学生通过解决真实情境中的真实问题，感悟数的运算之间的关系，体会数的运算在本质上的一致性，这有助于发展运算能力和推理意识。课堂上教师从运算意义、算理算法两个层面引导学生感悟小数乘法和整数乘法意义的一致性，对比单位换算法、面积模型法等多种方法，沟通算理与算法，揭示小数乘法与整数乘法运算在本质上的一致性，即转化为整数乘法来计算，从而优化了算法，发展了运算能力及推理意识。

[参考文献]

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2]刘坚，孔企平，张丹.义务教育教科书·数学（四年级·下册）[M].北京：北京师范大学出版社，2013：33-48.

[3]周冬梅，刘延革，李文会，等.将未知转化为已知，初悟运算的一致性：“小数乘法（第二课时）”教学实践与思考[J].小学教学（数学版），2023（9）：19-21.

[4]叶锡青，邵汉民.利用小数意义实现算理一致：人教版五上“小数乘法笔算”教学实践[J].小学数学教师，2023（Z1）：160-164.

（责任编辑：姜显光）