“述算”的内涵理解及实践路向

摘 要 《义务教育数学课程标准（2022年版）》（下称“数学新课标”）在小学计算教学方面呈现了明显的变化：重视了整体性和一致性，关注计算内容的前后整合和计算中思维的一致性理解。围绕整体性和一致性，从整个小学阶段的计算教学出发，对计算学习进行长程和多样的“述”活动，培养学生对计算学习的“领悟”“反馈”与“反思”的能力；在计算教学的实践中，通过对“述算”内涵的解析和发展价值的展望，探寻“述算”教学实践的整体路向。

关键词 计算教学 数学语言表达 “述算” 整体性 一致性

一、计算教学与计算的表达反馈

计算能力是学生学习数学所必备的能力，是贯穿于学生终生发展所必需的基本思维能力。就小学阶段而言，计算占据了数学学习内容的半壁江山。以“小学数学计算教学”为关键词在CNKI平台检索1980年至今的中文文献，可以发现2019年有关计算的研究处于高峰，然后回落；但随着2022年新课程方案及“数学新课标”的颁布，计算教学再次引起关注。研究主题均偏重于计算能力、教学策略和计算模式等，而对于如何培养学生用数学的语言来综合表达和反馈计算过程的研究缺少深度关注，基于小学阶段计算教学的整体性和一致性的学力提升专项研究也不多。计算常常以技能的形式外显于数学教学中，造成了很多教师只关注计算能力训练的价值，而忽视了学生在计算表述过程中思维互动、表达反馈等蕴含的潜在价值。小学数学计算教学也亟待从教师客体的“教”转向学生主体的“学”，让学生从隐性接受转向显性的主动共享。有鉴于此，本文基于计算教学的整体性、一致性和学生计算素养提升的视角，探究不同学段学生用数学语言表述计算过程及思维过程的特点和规律，即“述算”的特点和规律，以期更好地服务计算教学实践。

“数学新课标”提出了素养导向的“三会”目标，即：“会用数学的眼光观察现实世界”“会用数学的思维思考现实世界”“会用数学的语言表达现实世界”[1]。这三个目标分别对标了学生计算能力培养中的“关系发现和创新力培养”“数学运算和形式推理”“数据意识和模型意识”。可见，计算教学是实现“三会”目标的重要抓手，而如何“用数学的语言表达”计算是计算教学的应然需求。同时，在“数学新课标”11个核心词中，“运算能力”是唯一以“能力”作为属性来要求的，这充分凸显了计算的基础性和重要性，也意味着需要跨学段打通内容和思维的界限来提升学生的计算素养，从整体性、一致性的视角对计算内容和计算思维进行结构化的考察，关注学生的学程，通过“述”复现计算的过程和语言表达的质态，促进学生计算能力的高质量生长。

二、“述算”的内涵理解

“述算”指学生通过多种形式的数学语言表达对计算的发现和思考，达到计算思维的共享、争鸣与创新和促进学生计算能力自主和持续提升的目标。按照计算内容及叙述难度的不同，借用SOLO分类理论思想，笔者将“述算”分为三层进阶的内容结构。第一层内容是“述算程”，主要运用读、说形式表述口算过程，提高学生心算能力；第二层内容是“述算理”，主要运用笔算“阐述运算思考”，提高学生综合计算和运算理解能力；第三层内容是“述算律”，综合运用多种表达形式“交流、发现与创新”，培养学生对计算思维的深度解读的能力。“述算”的三阶内涵在层次上是递进的，三者彼此衔接，相互承载。

（一）“述算程”

“述算程”即一名学生先读题，然后紧接着说出思考过程和结果，另一名学生则对计算全过程进行监控、判断与评价（优化）。“述算程”主要用于口算、估算等简单的低、中年级的“心算”计算教学情境中。“述算程”活动可以在正式的学校课堂教学环境中进行，也可以在非正式的家庭、社会教育背景下实施。通过口述的形式，将隐性计算思维显性化，在记忆算式、读算口算、判断和优化反思中，发展学生的多元智能。

“述算程”实质是将“心算”外显成“口述”，将“心算”的过程进行“慢化”“细化”“柔化”，通过“读”“说”“评”将计算思维“研磨”“消化”“增值”。“述算程”重在培养学生用口述的形式表达计算过程中的思维状态。

（二）“述算理”

“述算理”是指在混合运算等稍复杂的计算和数量关系的运算中，通过笔算为主的形式让学生充分地表述出算理、算法和算序，并关联计算的“算术”和一般定理，在计算叙述中理解算理、明晰算法、理顺算序、优化“算术”、初悟“基本算律”，最后内化成个性化的计算思考。

“述算理”主要运用于中、高学段，重视算理和算法的联袂表达，促进学生对各种基础笔算的深度理解和基本关系思维的抽象与优化。

（三）“述算律”

“述算律”是学生先计算，然后再通过观察、思考，进而发现和表达出计算群组中蕴含的新思考和新运算规律，获得思维的跨越性增值。

在“述”中，学生通过合情或演绎推理形成新的计算模型，并借助模型发现和解决新问题。“述算律”将抽象、推理、模型、应用相互交融，在“算”与“述”显隐交互中唤起学生的好奇心、求知欲，发展学生的想象力，为学生计算创新力的发展植下后继生长的“种子”。“述算律”属于计算表征的高阶阶段，与学生创新能力密切相关。在计算群组的情境对比中，学生的思维方式灵活切换并集约化组合，走出计算思维的“困境”，主动寻找运算中规律的新模型。

三、“述算”的实践路向

围绕“数学新课标”中的“三会”目标，“述算”教学中有其自身的实施原则和方式。

（一）“述算”的实践原则

1.一致性原则。“述算”是学生计算学习的一种组织形式，在“述算程”“述算理”和“述算律”这三种形式中，都是以“述”的形式（口述、笔述）贯穿于计算全程。

“述算”活动的一致性要求在计算教学过程中：①用“述”来理顺计算的前提、思维、结论之间的一致的逻辑自洽关系；②表述内容的重心应放在算理呈现、思维表达及思维创新上，培养学生拓展思维的习惯；③在交流中，教师要引导学生从计算学习的困厄引至理解再到清晰表达上，促进思维自主且深度发展；④要在表达中使学生思维从个体隐性的“发生”变成群体显性的“发声”，“表里一致”，在争鸣与悦纳中走向计算的高阶思维。

2.整合性原则。“述算”从形式到内容都是整体构架：在组织形式上，活动小组通常采用两人或多人合作，以组内协助或组际合作的形式完成“述算”过程；在内容上，包含了小学阶段所有计算内容，通盘考虑不同学段计算内容的分布，形成基于计算内容的“三阶”整体结构。当然，内容亦可向幼儿园或者初中进行整体衔接。在对“述算”进行整体构架后，学生计算能力培养要能更多地指向能力以外的成长。例如，通过“述算”活动，让学生在沟通顺畅、人际关系和谐、运算热情释放、计算价值补偿、评价效果增值、群体计算内驱生长等方面，得到锻炼和成长。另外，利用“述算”整体化结构形式，让学习关系的赋权更具进阶性，即从自我为中心的学习到课堂合作学习，再升格为“去中心化”的信息高速交换的“无边界”学习。“述算”活动处于“教—学—评”周期的中、末端，通过让学生“述学”“述评”活动的真实反馈，达到以“述”引“教”，整体推进计算的“教—学—评”一致性的闭环增值。

3.层进性原则。“述算”活动具有层进性。“述算程”主要是借助口算（估算）来表达计算过程中的陈述性、程序性问题；“述算理”主要是通过笔算来表述算理、混合性的运算秩序和基本定律；“述算律”则要通过深度思考，发现并阐述复杂、整合性的计算规律，并用规律解决问题。“述算程”“述算理”“述算律”融入在不同学段，在计算教学中要分别呈现出“认识事实”“理解观念”和“像专家一样研究数学”三种递进的主体参与状态，形成“三位一体”的学生“述算”能力逐步提升的层阶结构。

4.思辨性原则。思辨性思维是一种系统性的思考过程，运用观察、体验、反思、沟通等多种方式方法，对事物进行认识、分析、辨别。因此，“述算”教学实践中培养学生的思辨性思维尤为重要。在“述算”教学实践中，有的老师在时间安排上缺乏稳定性和持续性；在教学内容安排上缺少整体前瞻性的目标指向，特别是缺乏长程的专项训练安排，或者有的只重视计算结果的判断，缺少思维过程表述的细化和深化；有时为了追求“述算”时效，只重视班级计算结论的统一呈现，而忽视了小组内平等个体的争鸣与创新，出现碎片化教学的现象。因此，在计算教学中，教师要重视“述算”的思辨性的呈现。

坚持“述”的常态与动态化实施，让思辨有时空，形成习惯；要重视面对面的计算多样化与抽象化的表达，让思辨有个性，激发创新；由点及面地培养学生的想象、推理、论证、理解表达等能力，让思辨有合力，懂得思维；将个体真实表达和集体智慧共“述”相互结合，让思辨有氛围，学会共享。

（二）“述算”的实施方式

1.“述算程”的实施。“述算程”主要针对口算和估算。笔者从14年前就进行了口算训练的关注与研究，实施主要过程为：（1）先准备一份口算题（无答案），孩子读题，再让其讲出计算过程和结果；（2）另一人（同学、老师或者家长等）看题、听读、核验，关注题目是否读错、计算过程是否简洁合理、计算结果是否正确；（3）“读算”结束后，另一人再进行反馈、修正、沟通。“述算程”活动可以在学生之间、师生之间、孩子与家长之间进行，对象多元、活动形式多样、学练兼修。

“述算程”活动是低年级老师经常采用的形式，在实践中可能会出现以下问题：缺少长程化的小组合作训练，或缺少计算过程中思维表达力的呈现，造成“述算”活动多浮于浅表或过于零碎。因此，口算表达活动中需要给学生更多元的“述算”时空，在计算表达的多样化和交流反馈的“慢”中增强学生的计算能力。同时，“述算程”训练实施中要关注计算资源使用的“智慧”：如口算题卡可横着读、竖着读、跳着读、倒着读、创编读等多种形式，丰富有趣的资源利用形式可以培养学生基于计算的细致观察力和多样化的思维表达能力。

2.“述算理”的实施。“述算理”主要针对小学中、高年级学段的混合运算及常见数量关系（如方程、比例）的运算，对计算的算理、思维方式和运算规律及策略进行介绍、反思、发现、共享、评介与争鸣。在“述算理”实施中需要关注以下几点：

（1）要注意计算过程的一致性表达，形成计算的整体理解力。以小数乘法[0.35 × 0.7]运算为例，其笔算过程如下：

0.35 × 0.7 =（0.05 + 0.3）× 0.7 = 0.05 × 0.7 + 0.3 × 0.7 =（5 × 7）×（0.01 × 0.1）+（3 × 7）×（0.1 × 0.1）= 0.035 + 0.21 = 0.245

在笔算中，通过“运算律（乘法分配律） + 计数单位”这两个核心概念的组合运算，小数乘法笔算算法初步形成。教师要进一步引导学生观察、思考，总结得出“计数单位的个数和计数单位的个数相乘，计数单位和计数单位相乘”。因此，乘法算式就可以直接变成 0.35 × 0.7 =（35 × 7）×（0.01 × 0.1）= 0.245，其算理意义就表示（35 × 7）个（0.01 ×0.1）这样计数单位的积，即数与量分别运算，数与数相乘，量与量相乘。

（2）要围绕数量关系的阐述，提升整体抽象和分析能力。“广义上的数量关系存在于数学的各个领域内容之中”[2]，因此，也要重视计算中数量关系的一般和抽象的“述”，建立关系间的关联。例如，在正比例量之间变化规律上，教师要引导学生从常量和变量变化特点上发现规律，初步体会计算中的函数思想，为初中方程、不等式和函数的学习奠定基础。

（3）要结合规律定理进行“实境化”表达，锻炼演绎推理能力。在关注抽象的同时，也要重视演绎推理的表达，即将计算方法、“算序”“算术”、基本运算规律的文本表达或字母式表达进行个例化联想并“反述”。例如“（a + b） × c = a × c + b × c，这个字母等式表示的关系，你可以联想到什么样的实际条件关系和问题？举例说一说。”通过对乘法分配律进行“实境化”联想，锻炼学生演绎推理能力。

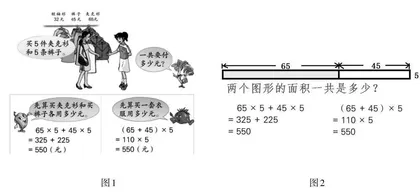
（4）要重视生活内容的具身融入，彰显情境计算的价值。“具身认知……把身体整合到现有的认知科学中，使它成为认知科学可处理的对象。”[3]计算教学要能让学生“沉浸”到真实情境中，包括生活情境、科学情境和数学情境。例如，在混合运算教学中，教材将运算顺序和运算律的教学置于买衣服的生活情境中（如图1），还可以置放于求图形面积和的数学直观情境里（如图2）。