整体建构：新课程标准下小学教学实施的新落点

《义务教育数学课程标准（2022年版）》强调内容的主题结构化整合。对教学内容进行整体建构，是数学学习的核心，可以将数学知识联结为一个连贯的整体。整体建构教学具有概括性、迁移性和发展性的特征，从而优化课程情境，推动学生深度学习的进行。本文以小学阶段“图形与几何”板块为例，从“大观念统摄”“结构化统整”“系统性统领”三个方面探析整体建构教学的策略，让学生的学习从浅层走向深度，从理解走向迁移，从低阶走向高阶，将思维引向整体化、结构化的高度，促进学生高阶思维的发展。

一、大观念统摄，基于知识内核建构关联

知识内核大观念往往居于数学知识点根部，具有生长力和生发力，也具有包容和浓缩的特质。“图形与几何”是小学数学中重要的教学内容。图形的周长、面积和体积的计算有着密不可分的联系，“转化思想”是链接它们的重要桥梁。利用“转化”的数学思想，可以打通学生“线、面、体”间的“隔断墙”，形成图形之间的联系，从而领悟到解决图形周长、面积和体积计算的通法、通理。

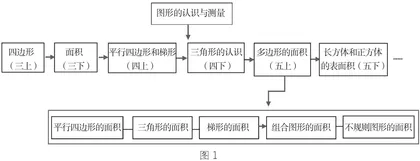
教师要引导学生逐渐形成大观念，首先应从探寻知识的内核出发。例如，人教版小学数学五年级上册“多边形的面积”这一单元，在关于图形面积的推理中，充分利用“转化”的数学思想，打通学生旧知与新知的“隔断墙”，把学生所研究的图形转化为已经学过的图形面积并加以运算。从探寻知识的内核出发，我们不难发现：平行四边形的面积是多边形面积的起始课，是本单元教学的一个“撬动点”。“平行四边形的面积”在“图形的认识与测量”知识链中前后关系如图1所示。

由图1展示的基于知识内核的关联可知，五年级上册“多边形的面积”教学，尽管是以“平行四边形面积”为起始课，但决定本单元教学质量的还取决于学生三四年级时学习的“四边形”“面积”“平行四边形和梯形”“三角形的认识”等基础知识内容的学习情况。 因此，在教学“平行四边形面积”的公式推导过程中，就要让学生充分回顾且掌握“什么叫作面积”“剪拼后的图形面积是否与原来大小一样”“长方形的面积公式怎样”“平行四边形有什么特征”

等。

学生掌握了以上基础知识的情况下，教师再重点引导学生以长方形面积的计算为基础，以平行四边形和长方形的内在联系为线索，以未知转化为已知的基本方法展开学习，让学生充分探究且观察发现“平行四边形可以如何剪拼成已经学习过的图形（如长方形）”“剪拼后的平行四边形与已经学习过的图形（如长方形）有什么联系”等。循序渐进、循循善诱，引导学生逐步掌握平行四边形的面积公式推导过程。

二、结构化统整，基于知识深度类化关联

在小学数学教学中，需要基于学科知识内在的逻辑关系与构成秩序将数学知识点进行融合，进而引导学生统整知识结构，并将之类化成认知结构。通过知识结构化，教师帮助学生把握数学知识的逻辑链，培养学生数学学习的探究兴趣，满足学生数学学习的成长需求。

在进行整体建构教学时，结构化整合，类化关联，拓展学生学习的深度。一般来说，可以根据目标、内容、方法和过程等类化知识。通过类化，原先分散的、零碎的、断裂的知识关联了起来，让数学教学呈现出一种整体性。例如，人教版五年级上册“多边形的面积”，就是在学生掌握了一般平面图形的特征，理解面积概念，掌握常见的面积单位，会用数面积单位的方法探究长方形与正方形面积的基础上展开学习的。基于对以上学情及教材的分析，教师可以把教学的主线设定为：认识图形的特征，掌握研究图形面积的一般方法，学会运用转化的思想方法推导出面积的计算公式，并进行知识的应用迁移。在此，我们不仅要激活学生的已有经验，更重要的是将学生的思考着力点回归到“度量”本质。因此“数面积单位”可作为本单元的“种子课”。平行四边形面积的计算是本单元的重点，本单元的“重点课”是利用转化的思想探究平行四边形的面积。在掌握了研究平行四边形面积的推导技巧之后，将三角形的面积和梯形的面积计算整合在一起，三角形和梯形的面积推导过程具有很强的关联性，因为，通过类比，学生便能更好地完成对知识的理解与应用迁移。这样，依托教学主线，完成了对课程的整合。具体见图2。

教师对本单元学习内容进行“向内深挖”，并建构其多边形面积单元的概念地图、单元结构和序列，深度认识单元设计的理念和步骤，从而找到单元的本质问题和关联所在。 因此，当学生充分理解和掌握 “平行四边形面积公式”的推导过程后，不仅能深度掌握知识和技能，还能充分掌握知识的由来和运用规则，有效激发学生对数学的探究乐趣，并有效促使和帮助学生对随后学习的三角形和梯形的面积公式推导的学习与探究。 这一方面让学生学会运用“类化”的思想方法，借助未知与已知知识的共性和内在联系，掌握未知的知识与方法，积累数学活动方法与经验；另一方面，在获得新知识的同时，进一步发展空间观念。

其次，让学生这样体验“结构化统整，基于知识深度类化关联”教学，可让学生切实掌握“多边形面积”转化方法和类化关联的关键所在是自主构建“推理”和结构化统整的模型。随着学习的深入，学生从不同角度对问题进行分析，运用多种方法推理、解决问题，并在自主推理的过程中，发展学生的高阶思维。

三、系统性统领，基于知识拓展延伸关联

为更进一步促进学生数学素养的发展，从数学知识的有机整体和学生思维发展的视野进行整体建构教学，促进知识的结构化和学生思维的进阶，教师还应该引导学生以“望远镜”的思维方式对单元内容“向外扩展”，充分考虑其他单元、甚至是其他学科等方面的知识构建“从宏观到微观”的“系统性统领”的整体框架 。引导学生用“望远镜”的思维方式，从具体学习单元出发，建立与其他知识的联系，从而形成结构化的数学知识体系，有助于学生寻找运算单元知识的内在联系，从而提升思维的深刻性。

就数学应用而言，教师不仅要在分析知识的基础上引导学生学会应用，还要对相关知识和学习过程进行统整，让学生感悟数学思想方法。例如，“平行四边形的面积”一课，从结构化教学的实践意义看，全课设计围绕清“面积”之意义、破“底边×邻边”之误判、找“转化之关键”、理“比较”之思路、导“推理”之表述、练“公式”之应用、辩“底高”之对应、拓“等底等高”之认识为主线环节，让学生经历逻辑推导的严谨过程，体会数学思想方法的同时，发展学生的高阶思维。指向性的系统知识建构，让逻辑层层递进，帮助学生建立起前置知识和后续学习之间的互联互动，为建立良好的认知结构奠定基础。

图形与几何整体建构教学的关键，在于沟通知识结构上的内在联系，经历数学思维过程，感受并掌握转化的数学思想，从而建立整体的“知识链”和“知识面”，建构起图形与图形间的关系模型。