有“感”而量,入“悟”三分

一、观课所见：“潜意识”的比较

一次活动中，聆听了人教版小学二年级《角的初步认识》一课，教师用微课“切蛋糕”引入，再借学具“百变扣条”制作活动角，以求让学生感受并发现“角的大小与边的长短无关，与张开的大小有关”规律。

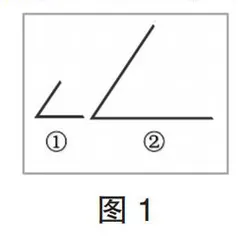
然而，教学过程看似“完美”，学生却在练习中暴露了问题。当提出“两个角的大小怎样？”（如图1）时，大多学生毫不犹豫地说：“第二个角大。”尽管一再动态演示、重合比较，但仍有学生认为第二个角比较大。

笔者回想教学四年级《角的度量》时，学生虽知用度量比大小，但潜意识里仍会认为第二个角大;甚至到了六年级学习《图形的放大与缩小》后，做“用10倍的放大镜去看一个角，则角的大小（ ）。A. 放大10倍;B. 缩小10倍;C. 不变。”此类题时，仍会出错。

二、剖析所思：“误判断”的因由

带着疑问，笔者从数学分析、认知分析、教学分析三个维度加以剖析，探寻因由。

（一）全方位“数学分析”

角是一种几何对象，不同版本教材的编排不同。小学人教版教材主要把角的知识编排在二、四年级，中学则分初中和高中两阶段学习，不同阶段其定义不一。

对于角的初步认识通常安排在二年级，其流程如下：

显然，这样的过程是循序渐进的，但此阶段定义并没界定角的大小本质，甚至四年级以“从一点引出两条射线所组成的图形叫做角”来定义，也只停留在“图形”领域，没涉及“量”的范畴。同时，人教版教材没用“短弧线”来表示角，这不利于学生对“角的大小”这一“量感”的建立。其实，角的动态定义更能揭示角的大小的数学内涵——对两条边（射线）的方向之间关系。

（二）多角度“认知分析”

为何学生会坚持认为图1中第二个角比第一个角大，甚至到了小学中、高年级仍会出错？笔者通过访谈、反复调研，发现了问题所在。

1. 前期经验习惯的影响——误整体比较

认识角之前，学生已形成从整体上比较图形的大小、线段的长短、物体的数量等习惯，且与生活经验基本一致。故在比较角的大小时，学生会顺理成章地误从整体上把“两条边及其所夹区域”想象成相应“三角形”来比较（如图2）。

2. 抽象辩证思维的缺乏——难理解大小

对于数量、长度、面积、体积的比较，因其“量感”对象真实存在，且生活中处处有相应看得见、摸得着的实体，故易理解。但在小学阶段，“角的大小”主要是指“角的两边张开的大小”。“张开”是动态的，而“角的定义”只是静态的象形性描述，用一个“新概念”解释另一个“新概念”并非易事。特别是当“边”无限延长时角的大小仍不变，对缺乏抽象辩证思维的二年级学生而言，难以理解。

（三）深层次“教学分析”

1. 内容上没有依本质取舍

学习困惑的形成、量感的缺失，也与教学相关。在受访的30名数学教师中，有92%的教师并没有意识到人教版教材未涉及“角的大小”的本质。教学中，只是照本宣科，当学生发生误判时，仅通过反复演示及讲解等措施来“补救”。但“补救”后，部分学生仍“一如既往”地误判角的大小。

2. 形式上没有循逻辑推进

关于角的含义，大多教师认知偏离，没真正考虑知识生成、学生认知的规律，也没有设计有效教学活动来逻辑推进，导致学生对“角的大小”理解不到位，难以从根源上辨析影响其大小的因素。

三、实践所得：“聚核心”的解困

图形作为几何的对象，需研究图形的大小以及图形之间的关系，而角作为一种几何图形，与测量密不可分。因此，教学“角的大小”时不仅要关注图形的认识，更要关注其功能价值，以及“量感”的建立。笔者针对二年级学生就“角的大小”这一量感的培养进行实践尝试。

（一）量形结合，唤醒“量感”直觉初感悟

1. 从“生活原型”抽象出角

图形从现实中来。课始，出示两组物体（如图3），让学生从“静态”“动态”两个角度去摸一摸、找一找角。

在这个过程中，直观了解“什么是角”，初步感悟“角有什么用”。接着，把学生在学习单上所描的“不规则的角”抽象为“规则的角”，顺势指出“这些图形都是角”，明确其组成要素——一个尖尖的顶点、两条直直的边（如图4，暂不标注“弧线”）。再比较两组物体中的角，发现“钟面上时针与分针”等所形成的角是可活动、变化的（如图5），为后续探究“角的大小”作铺垫。

2. 由“比较大小”唤醒直觉

课中，以熟悉的“嘴巴”到常见的“剪刀”，引发学生联想到角就像“张开的口”，思考“为什么剪刀形成的角会有变化”。

生1：剪刀张开的口有大有小。

生2：两边张开的口的大小不同，角的大小也不同。

师：那怎样比较角的大小？

生3：看两边张口的大小来比较。

生4：张开的“口”大的角就大，张开的“口”小的角就小。

教师结合课件并作小结（如图6）。

可见，利用量与形的结合，寻找钟面、剪刀、嘴巴通过张开所形成的“动态”角，可唤醒学生对角的“量感”直觉，并结合“具身经验”有效实现对“量感”的关注，初步感知“角有大小之分”及比较方法。

（二）表征外化，建立“量感”表象揭本质

1. 依功能价值“制作”活动角

上述案例虽用比喻激活了学生对角的量化经验与直觉，但具体比较方法仍不够清晰。为此，笔者提出“造角”分层活动（同桌各用绿、橙长短不同的磁条来操作）。

①“造”角：随意制造一个角;

②“变”角：转出大小不同的角;

③“比”角：比一比，谁的角大？为什么？

这样，让学生真切体会到利用“旋转”可以使角的两边“张开”与“收拢”，增强对角“大小变化”及“比较方法”的感悟。

2. 据形成路径“外化”角大小

角是采用“弧度制”测量的，而“短弧线”这一符号在清晰外化其“量感”对象的同时，可有效彰显其测量内涵。故在依功能价值“制作”活动角后，笔者顺势揭示“<TPL：G：＼广东教育（综合）202208pdf＼广东教育（综合）202208＼原文件＼8JY44-58.fxpkg＼叶巧如-.tif>”的意义——

师：比较角的大小时，实际上是比较哪一部分？

生（齐）：比较角张开的口。

此时，趁机用“<TPL：G：＼广东教育（综合）202208pdf＼广东教育（综合）202208＼原文件＼8JY44-58.fxpkg＼叶巧如-.tif>”标注出各个角（图9），指出短弧线的作用，明确对角的研究主要看它的张口。这样，从模糊的具身经验走向清晰的符号表达，有效建立对角的“量感”表象，并加深体验。

（三）活动思辨，厘清“量感”属性深体会

1. 旋转活动：“边的方向”变化→“角的大小”随着变化

通常，学生到四年级才接触角的度量，但角的大小实质上是角的度数，边的张开与收拢是因“方向改变”而致。如何针对二年级学生适度切入以填补现行教材与教学的空白？笔者基于学生认识了钟面、旋转等知识，尝试借助钟面活动，让学生感悟角的变与不变。

师：橙边和蓝边分别表示时针和分针，现在指向几？（图略）

生1：两边都指向“12”。

师：如果橙边位置不变，蓝边有什么变化（课件动态演示蓝边绕顶点从“12”旋转到“1”）？

指名学生回答后，把“大头儿子”和“小头爸爸”头像放在蓝边上，蓝边继续旋转到“2”（课件演示），提出：现在，两人的位置怎样？

生2：两人的方向同时变了。

生3：方向变了，原来指向“1”，现在指向“2”。

……

接着，蓝边继续旋转，引导学生观察“大头儿子”“小头爸爸”的位置，分析发现：两人方向同时改变了（从指向“12”到“1”再到“3”），但旋转时，他们始终都在同一条边上。

显然，从具体活动到抽象图形，再到学生的心理图式，可帮助学生深刻感受到角的大小就是方向的改变程度，则“边的方向”改变“角两边的张口”大小，则角的大小随着边的方向变化而变化。

2. 伸缩活动：“边的长短”变化→“角的大小”不变

角的功能价值在于“两边张开的大小量化”，而两边的长短并非要义所在。为揭示角的大小与边的长短无关，笔者利用课件演示蓝边延长与缩短（如图10），蓝边上“大头儿子”“小头爸爸”“围裙妈妈”的方向不变都指向“2”，故角的大小不变。

这样，通过辨析影响角的大小的关键因素，从本质上悟透角的概念，避免受图形的外在因素困扰而误从整体上比较。

（四）动态链接，助推“量感”形成促内化

1. 先“估”后比，形成量感

为更好地帮助学生建立对角的“量感”，在直接比较之前可先行“估测”（如图11），再比对“验证”，以引发学生对角的大小“量感”表象信息的适切提取，增强“量感”意识。

事实上，学生会经历“初选比划→实地对比→调整再比”的思辨过程。特别是根据屏幕的角选择三角板相应的角去比划，与到屏幕前实地对比发现有误时，学生会调整再比，直到正确（如图12）。此时，教师相机提出：“你们的小三角板放在屏幕中，看似比较小，但为什么角的大小一样？”“如果用老师的大三角板呢？”（如图13），引发思辨，聚焦到“角的内部”，明确得出结论：虽然三角板的大小不同（即不管是用学具小三角板，还是教具大三角板比较），但只要对应角的张口一样，角的大小就相等。

2. 后“知”前移，深化量感

虽然“角的度量”在四年级学习，但基于整体认知，可选取“角的度量”部分知识制作成微课，作为阅读与了解的拓展材料，让学生初步感知，避免片面认识角的大小，再通过适度拓展与整合，让学生建立更清晰、更灵动的角的“量感”。

教师还可根据学生的实际情况，课后推送有关“角的大小比较”的数学绘本供学生阅读，激发学习动力，培养学习能力，开发学习潜力。

诚然，教了≠学了，学了≠学会。综上所述，若只是想当然地“教”，而不综合考量实际，那“学”就难以有效落实。本文围绕角的“图形的认知”“功能价值”双向设计教与学，以“深度教学”引领“有效学习”，在指向学科知识的同时，聚焦核心素养，促进思维发展，从直觉唤醒、表象形成、属性厘清来助推角的“量感”建立，让学习真实发生，提升学生的学习力。

注：本文系广东省教育科研“十三五”规划2020年度教育科研一般项目“指向学习力提升的小学数学任务驱动式教学的实践研究”（课题批准号：2020YQJK205）研究成果。

责任编辑 罗 峰