高中数学二次函数建模能力培养

随着数字化发展以及科学技术的进步，数学知识应用范围不断扩大，相关应用内容变得更加丰富，这对现代人才的建模素质与能力提出了越来越高的要求。高考数学试卷中考查学生数学建模能力的题型是必考题，但是如果高中生本身缺乏数学建模思想，会直接影响他们数学解题能力的发展，同时也会限制他们的实践操作能力以及核心素养的养成。其中二次函数是高中数学教学中一类非常重要的函数，相应的二次模型建构能力关系学生能否顺利解决二次函数问题。

一、数学二次函数建模能力培养的价值

鉴于农村地区教学条件有限，师资力量不足等问题较为突出，直接影响了高中生的数学知识学习效果。为了提高学生学习数学知识的效果，必须持续提高学生的数学学习能力。其中二次函数题型是高中数学教学中的重要题型之一，主要是围绕二次函数，再联系人们的生活实际，构建生活化的数学问题。函数题型主要考查学生对函数知识的理解与认识以及他们运用二次函数知识求解实际生活问题的能力，力求达到“学以致用，学以活用”的目的。纵观以往的高考数学函数题型可知，其可以同利润、物价、人口、产量以及路程等生活化实际问题有机结合，构成生活化函数问题。而数学建模思想是高中数学核心素养培养的题中之义，关系学生能否灵活应用所学函数知识来解决实际生活问题的能力。因为任何一道贴近生活实际的函数问题，经过建模思想的运用，可以从中构建出对应的函数模型，使学生应用所学函数部分的知识，便捷、快速地求解问题，极大提高了学生解决实际问题的实践能力，助力高中生数学核心素养的养成。

二、数学二次函数建模能力培养的基本思路

二次函数是高中数学学习阶段非常重要的一类题型，本身是函数知识和实际生活问题的有机结合，综合性与繁杂性比较强。在将数学建模思想应用于高中二次函数题型求解时，必须明确基本的应用思路，主要可以归结为如下几个步骤：

第一步，挖掘和分析问题。在解决二次函数题型期间，要首先认真阅读题目，明确已知解题条件和待求问题，搞清楚所求问题的求解本质以及数学问题中涉及哪些类型的函数知识。

第二步，建立和求解模型。在搞清楚待求二次函数题型的求解信息基础上，需要从中归纳、总结出其中所涉及的二次函数模型，包括明确二次函数模型的基本变量参数，确定函数的基本求解信息等。而在构建二次函数模型期间，还要注意综合考虑化归思想、分类讨论思想等一些数学思想，避免单纯应用数学建模这一单一数学思想而影响最终数学模型构建的效果。

第三步，检验和应用模型。在构建求解数学问题的数学模型基础上，需要调用相应知识来解决数学函数问题，再联系实际快速求解问题。

基于上述三个数学建模思想的应用过程，可以在分析待求解二次函数题型的过程中经历问题分析、模型建构与应用几个关键的解题过程，最终可以快速找到解决问题的突破口。

三、数学二次函数建模能力培养的有效策略

（一）应用于方程和不等式问题解决

二次函数建模构建的基础是学生对二次函数的性质、图像特征等方面知识形成深刻认知，并在此基础上有效结合具体的问题来开展深入剖析，找出其中包含的二次函数部分知识，力求借助二次函数模型建构提高学生的二次函数建模能力。在二次函数问题剖析中，由于涉及不等式、方程与函数等多方面内容，所以求解中可以针对性选择相关问题来开展深入剖析。

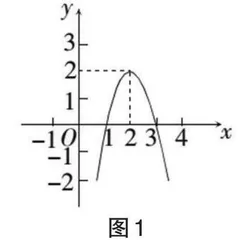
例1：如图1是某一二次函数的图像，结合给定图像求解如下问题：

（1）求解二次函数的两个根；

（2）试求ax2+bx+c＞0这一不等式的解集；

（3）伴随x的增加，y值不断减小，试求x取值范围是多少？

（4）假定方程ax2+bx+c=k，总计2个不相等的实数根，试求参数k取值。

解析：针对本道二次函数类型题，在求解中需要学生认真分析，尤其是要明确问题求解中包含的二次函数性质、图像特征等方面知识，避免因为无法深入剖析问题而直接影响了问题的顺利求解。函数概念是认识函数的基础，由于高中阶段涉及指数、对数、三角函数等几类函数，并且不同类别函数的概念有所不同，这使得各种函数题型在求解中必须明确相应的函数类型及概念，之后才能在此基础上有效构建及应用相应的函数模型。

解：针对问题（1），可以结合图1中二次函数与x轴之间的交点来确定相应的答案，即：x1=1，x2=3。针对问题（2），可以在构建模型中同样结合图像性质，明确其实际上是x轴之上部分，故相应解题答案是1<x<3。针对问题（3），为了保证随着x值的增加而使得y值出现变小的情况，主要表现为“减函数”，这就需要做到对称轴的右侧，即正确答案是“x>2”。针对问题（4），在构建二次函数模型过程中，可以将等式左边看作是一个二次函数图形，等式右边可以看成y=k这一平行于x轴的直线，为了保证二者相交过程中保持2个不同的点，必须要保证y=k这一直线本身同函数图像之间呈现为2个交点，即k<2。

（二）应用于方程组求解问题

二次函数模型建构的根本出发点是借助模型建构来帮助学生调用二次函数部分的知识对问题进行剖析与解决，帮助他们可以更加高效、准确掌握所学知识点。方程组求解也是高中生常见的一类问题，以往的问题求解可能会采用常规求解方法，但是二次函数的方程组求解可能会涉及到较多步骤，工作量相对较大。而如果可以指导在对方程组问题进行求解中创新运用二次函数模型建构思路，那么可以帮助他们快速简化问题。

例2：如图2，现有一二次函数ax2+bx+c=k的抛物线图像和x轴相交在A点与B点，和y轴相交在C点，其中顶点是P点。已知A点和B点横坐标分别是-3和1。

（1）试求参数m和n；

（2）试求直线PC解析式。

解析：针对本道二次函数问题的求解，如果直接采取常规的解题方法，那么整个解题过程比较复杂，但是如果可以指导学生在对问题进行剖析与求解中创新融合二次函数建模思路，那么能够对相应问题进行快速求解。

解：（1）基于题干信息，可知二次函数本身经过了A（-3，0）和B（1，0）这两个点，故可知：

求解可知m=1，n=-3/2。

（2）由于y=[12]x2+x-[32]，故可以确定P点与C点的坐标，假定直线PC解析式是y=kx+b，这样可知：

求解可知：k=1/2，b=-3/2。

如此一来，就可以对直线PC解析式进行确定，具体就是：y=[12]x-[32] 。

基于上述解题可知，在对二次函数问题进行剖析过程中，方程组求解本身同二次函数图像交点坐标之间关系具有非常紧密的联系。在指导学生学习和利用二次函数模型建构方法期间，必须要注重指导学生熟练掌握方程组求解方法，尤其是要使学生对二次函数、方程之间的紧密联系进行明确。

（三）应用于生活实际的问题解决

为了对学生的二次函数建模能力进行有效锻炼及提升，需要指导学生灵活运用该种建模能力，简化学生求解问题的思路，使他们高效解决有关二次函数问题。

例3：现有一农场要修建养鸡场，为了节约养鸡场建设的材料，鸡场一边背靠着一堵长度足够的墙，其余部分则选择应用长度30m的竹篱笆进行围建。现在建设过程中总计包括如下两种建设方案：其一，针对方案一，主要是围成图3的一个矩形；针对方案二，主要是围成图3中的一个半圆形。假定矩形面积是S1，宽是x，半圆形面积是S2，半径是r，试计算该选择哪种建设方案来保证养鸡场面积建设达到最大值（π≈3）。

解析：针对本道问题而言，主要是现实生活中常见的一类实际问题。基于现实生活中这些问题的设计主要是考查学生的二次函数应用能力。针对二次函数模型有效构建，能够将本道实际的生活问题进行抽象化表达，使学生灵活运用二次函数模型建构方面的知识来对整个问题进行剖析，并在这个过程中对所涉及的问题进行有效解决。

解：

在x=15/2的时候，S1值达到最大值，最大值是225/2平方米。

基于30=πr，可知r=10m，这样可以求得S2=1/2×πr=150平方米。

如此一来，可以发现本道题的正确答案就是选择方案二来保证竹篱笆围成的面积达到最大值。

（四）应用于数学综合问题解决

在指导学生有效运用二次函数建模知识求解问题中，除了单纯考查二次函数问题外，同样要紧密联系一些综合性问题来拓展学生思路，让学生融合函数性质，将二次函数建模意识逐渐拓展到一切函数的建模方面。在相应的函数题型求解过程中还会涉及转化、化归等一些数学思想，需要综合调用相关数学思想来简化函数问题分析及求解过程。

例4：现有一函数<J：＼2024智慧教育＼3＼内芯＼6.14-7.jpg>，试根据如下条件求解相应的问题：

（1）在参数a=2时，求令f（x）=x成立的x的集合；

（2）试求函数y=f（x）在y=f（x）上的最小值。

解析：本道例题是一道综合运用函数知识和导数知识的问题，问题（1）主要是考查对x进行分类讨论来去掉相应的绝对值符号，这样就可以得到明确的方程，之后可以再求出其值；问题（2）则主要对a进行讨论，结合函数一阶导数值来对函数于区间上面的单调性判断函数的最值。在求解这道函数题的时候需要结合函数的单调性质来构建对应的函数模型，并加以求解。

解：（1）基于题干信息，可知 <J：＼2024智慧教育＼3＼内芯＼6.14-7.jpg>。

在x＜2时，f（x）=x2（2-x）=x，求解可得：x=0或x=1；

在x≥2的时候，f（x）=x2（x-2）=x，求解可得：x=1+[2]。

综上所述，在参数a=2时，令f（x）=x成立的x的集合为{0，1+[2]}。

（2）假定相应最小值是m，

在a≤1的时候，在区间[1，2]上面，f（x）=x3-ax2，进而可得：

由此可知，函数f（x）=x3-ax2在区间[1，2]上面是单调递增函数，故可知：

在1<a≤2的时候，在区间[1，2]上面≥0，基于f（a）=0可知

在a>2的时候，在区间[1，2]上面f（x）=ax2-x3，此时

假定a≥0，在区间（1，2）上，故可知在区间[1，2]上面f（x）=ax2-x3为单调递增函数，故可知：

在2<a<3时，可知1<[23]a<2，当1<x<[23]a时可得，故可知此时f（x）在区间[1，[23]a]上为增函数，此时可知：

在[23]<x<2时，也可以确定f（x）在区间[[23]a，2]上面为减函数，所以可知：

在2<a<3的时候，

在2<a≤7/3的时候，

在7/3＜a＜3的时候，

综上所述，本次所求函数的最小值如下：

上述这道函数题型本身的综合性比较强，针对这种比较复杂的函数题型，要本着“化繁为简，逐个攻克”的思想，尤其是在遇到包含绝对值的题型中，要通过灵活运用分类讨论思想来逐步去掉绝对值符号，之后再进行问题求解。

总之，二次函数建模能力培养是提高高中生解决函数问题的一种教学手段。在培养高中生二次函数建模能力期间，可以紧密结合不等式、方程组求解等方面问题强化学生对二次函数性质及图像等方面知识的认识，联系生活实际，指导学生运用二次函数建模能力来简化数学问题，促进学生二次函数建模能力的发展。