溯源、对应与变式

“数学广角”属于数学课程中用以开阔学生的数学视野、激发学生的数学学习兴趣的拓展部分，其宗旨是贯彻课程标准理念，有系统、有步骤地渗透数学思想方法。人教版小学数学教材五年级上册的“植树问题”在各地各类教学展示观摩中，一直有着较高的“出镜率”。学生学习此类问题要经历抽象、推理与建模的过程。从现实情况来看，学生对总长、段长与段数的关系比较陌生，特别是学困生，当他们把注意力集中到是否需要“加1”“减1”的思考上时，常常不知道段数该怎么求。为提升学习有效性，教师需要教学寻根与优化设计。

一、教学寻根，找到教学路径中存在的不足

（一）结构断片，新知识学习不扎实

“植树问题”有多种变式（两端都种、只种一端、两端都不种、环形栽种），教师通常把教学重点放在对植树问题各种情况的识别上，看起来似乎是对症下药，但实际效果并不理想。就像要清理四散的水流，如果是流到哪里堵哪里，那一定是手忙脚乱的，只有把源头清理好了，才能从根本上解决问题。

“把新授课当作复习课来教”，这是当下教学设计的一种新理念。其实质就是最大限度地缩短新知识与旧知识之间的距离，让学生感受到新知识不新、新知识不难。以这种理念为指导的教学设计最一般的策略就是对新知识进行溯源，与旧知识进行对接。“植树问题”的源头实际上是学生已经熟悉的平均分模型：总数÷每份数=份数，“植树问题”中的总长度就是模型中的总数，“植树问题”中的间距就是模型中的每份数，只不过，我们在平均分的模型中（以线段图为例）重点关注了最后得到的份数（段数），忽视了平均分所分的次数（点数）。

（二）表征不清，一一对应关系模糊

笔者做过一次“植树问题”的教学前测：在一条20米长的小路一边种树，每隔5米种一棵（两端都种），一共需要种几棵树？（请先画图再计算）在未做任何其他提示的基础上，整个班级的学生解答问题的正确率可以达到80%。很多学生能正确画图，并能列出综合算式：“20÷5+1=5（棵）”，当笔者问道：“前面20÷5=4，这个4与后面4+1=5（棵）中的4，这两个4意思一样吗？”有的学生说一样，有的学生说不一样，很少有学生能给出正确解释。

学生解答问题的正确率高是因为后面有先画图再计算的提示，学生从线段图中可以较为直观地看出答案，20÷5后面再加1大都是根据图想到的，而不是对算理的掌握，所以这里存在着认知误区。“在一个算式的计算过程中，同一个数要有两种不同意义的理解并进行切换。”在此之前学生没有相应的认知经验可以作为支撑，所以综合算式实际上省略了学生在本题中最需要解释的“一一对应”这一重要关系。

（三）辨析匮乏，练习设计不够丰富

“植树问题”的题型变化很多。以“两端都种”“两端不种”“只种一端”这3种基本模型为例，每一种模型都包含了3个（或以上）相关联的量，将这3个（或以上）相关联的量再各自转化一下，就可以变出9种（或以上）不同的数量关系。平常一般的教学设计多为不同情境的变式或不同模型的变式，没有突出不同数量关系的变式。

需要让学生清楚的是，变式题不管怎么变，解题的基本思路是一致的，就是先要确定求“总数”，还是求“段数”“点数”。因为这个延用的是平均分的模型，学生可以从整体上把握解题的基本结构。然后再看是哪一种模型，是要“加1”，还是“减1”或是“不加不减”。还有一点非常重要，我们是通过画线段图的方法对基本算理进行探究的。

二、优化设计，通过溯源、对应与变式帮助学生有效建模

笔者认为，教学“植树问题”时要使学生能有效建模，教师需要向下扎根，唤醒学生的学习经验，以获得生长的营养与力量。开始的列式解答需要分步进行，突出“段数”转化为“棵数”的过程，让算理更加清晰；练习的设计需要整体呈现，加强学法点拨。

（一）问题导入，激活经验

1.出示材料，解决问题

师：在生活中，有这样两个数学问题，你会解答吗？

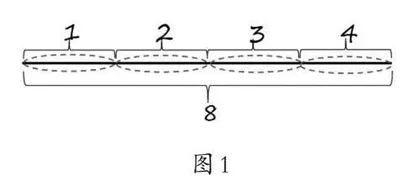
（1）一根竹竿长8米，每2米锯一段，可以锯成几段？

（2）一根竹竿长8米，每2米锯一段，需要锯几次？

师：请同学们先画图，从图中找出结果。

（生画草图，师选择性呈现）

2.反馈交流，辨析异同

师：看看这些图（如图1、图2），说说你是怎么想的。

生：第（1）题可以锯成4段，第（2）题需要锯3次。

师：4在哪里？3在哪里？你能在图上标注出来吗？

（学生将“段”与“点”标注清楚，如图1、图2所示）

师：这两个问题有什么相同点与不同点？

生：它们都锯成了4段，都是每2米锯一段。

生：它们的总长度都是8米。

生：它们一个是锯几段，一个是锯几次。

3.提炼本质，揭示课题

师：把8米长的竹竿以2米分一段，这是在干什么？

生：在平均分。

（板书：平均分）

师：它们都是把竹竿以同样长度锯成几段，不同的是第（1）题求的是分隔的段数，第（2）题求的是分隔的点数。这类研究段数与点数的问题，数学上称为“植树问题”。

【思考】“植树问题”的学习起点是平均分。借助线段图，明晰两个问题的异同，唤醒学生原有的学习经验。以前学习的平均分是“分段”，而“植树问题”的平均分是种“点”。

（二）突出对应，建立模型

1.出示材料，理解题意

教师出示问题：在一条长20米的小路的一边种树，每隔5米种1棵，一共要准备多少棵树苗？

师：读一下这道题，请找出你认为重要的信息。画一画，算一算，把想到的几种情况都记录下来。

【思考】有了课始的题组铺垫，新授环节，教师用一道开放题引发学生思考，培养学生收集信息与分析信息的能力，培养思维的完整性。

2.自主探究，组内交流（略）

3.整体反馈，分类探究

师：在刚才的小组交流中，我收集了下面这些不同的做法（投影呈现，并附图）。

（1）20÷5+1=5（棵）；（2）20÷5-1=3（棵）；（3）20÷5=4（棵）；（4）20÷5=4，4+1=5（棵）；（5）20÷5=4，4-1=3（棵）。

师：观察这些不同的做法，你有什么发现？

生：（1）和（4）实际上是同一种思路，（4）是（1）的分步列式；（2）和（5）也是同一种思路，（5）是（2）的分步列式。

生：这里有3种不同的答案，有5棵、3棵、4棵。

师：同一道题怎么会有3种不同的答案呢？

生：情况不同，有的是路的两端都种，有的是两端都不种，有的是只种一端。

（1）交流两端都种的情况

师：大家的列式中都有“20÷5”这一步，这个算式是什么意思呢？ 谁来结合图3说一说。

生：20米是总长度，每5米分一段，可以算出有这样的4段。

师：后面部分“4+1=5（棵）”中的“4”是带什么单位名称？

生：“4”后面的单位名称是“段”。

生：不对，“4+1=5（棵）”中的“4”单位名称是“棵”，因为最后结果是5棵，只有4棵加1棵才是5棵。

【思考】学生认为“4+1=5（棵）”中的“4”是从前面“20÷5=4段”中延续过来的，因为前面一步中“4”的单位名称是“段”，所以后面一步中“4”的单位名称也应该是“段”。但随即对最后的“5棵”这个结论，学生马上又进行了“否定”，这个问题是我们最容易忽略的思维盲点，搞清楚单位名称实际上就是对算式意义的本质理解。

师：我们知道前面“20÷5”计算出4的单位名称是“段”，但后面“4+1=5”算式中“4”的单位名称怎么就变成“棵”了呢？

生（边说边比画）：从图中我们知道，“1棵树与1个间隔”也就是这样的一段为一组，共有4组， 所以“4段”也就是“4棵”。

师：原来“4段”对应了“4棵”。

（师补充板书：4段→4棵）

师（指向算式）：“20÷5=4（段），4段→4棵，4+1=5（棵）”，后面为什么还要再“加1”呢？

生：把“1段”与“1棵”看成“1组”，这样有“4组”，最后还多出“1棵”。所以要“加1”。

师：谁来把这样一组一组对应的情况清楚地表达出来？

（学生画出表示“棵”与“段”对应关系的“弧线”，圈出表示剩余的“1棵”树）

师：刚才我们交流的是路的两端都种树的情况。

（2）交流两端都不种树的情况（过程同上，略）

（3）交流只在一端种树的情况（过程同上，略）

（4）小结，整理板书（如图4）

【思考】学生通过画图获得“段数”与“棵数”之间对应关系的直观感知，但这种直观感知只是方便学生算出答案。教师要让学生充分理解每一步列式的正确含义是什么，算式中的“段数”与“棵数”在什么时候发生了变化。最后，通过整理结构化的板书，使学生获得一种新的认识：这三种情况都是同一个数量关系根据具体情况派生出来的不同变式。

（三）模型应用，培养思维

1.联系生活找原型

师：如果把一棵一棵的树变成一个一个的点，那么就变成了一幅幅线段图（如图5）。生活中这些点可能会代表什么情况？

生：可能是装路灯、停车场停车、学生列队……

2.根据情境辨类别

师：课始的锯竹竿，属于“植树问题”的哪种情况？

生：两端都不种。

教师出示材料：（1）一列8米长的队伍，每隔2米站一个人，这列队伍一共有多少人？

（2）在600米的城市道路上摆放垃圾桶，每100米放一个（路的起点不放），一共要放几个？

师：列队与摆放垃圾桶分别属于哪种情况？什么相当于“树”？什么相当于“间隔”？

……

3.题组解析 ，加强应用

教师出示题组，学生独立解答。

（1）学校一楼有一条长30米的走廊，沿着走廊的一边每隔6米摆一个展示牌（走廊的两端都不摆），一共需要准备多少个展示牌？

（2）在校门前小路的一侧，共安装5盏路灯，路的起点是公交站牌，不安装，这条路全长100米，平均每盏路灯之间相距多少米？

（3）中午就餐，6名同学在等候区排队，每两人之间距离为0.5米，这个队伍全长是多少米？

4.比较分析，加深理解

教师出示学生第（1）题的解答：30÷6-1=4（个）。

师：大家有什么问题吗？

生：两端都不摆，为什么不“减2”而是“减1”呢？

生：两端都不摆，段数比点数多1，30÷6算出5段，所以最后要“减1”。

师：如果“减2”的话，是什么情况？

生：要先算出两端都是摆几个，然后再“减2”。列式是“30÷6+1-2=4（个）”

师：“30÷6+1-2”实际上就是“30÷6-1”。

教师出示学生第（2）题的解答：100÷5=20（米）。

师：算式中的“5”是什么意思？是“5盏路灯”吗？

生：是“5个间隔”，在只安装一端的情况下，间隔数与路灯数一一对应。

教师出示学生第（3）题的两种解答： 6×0.5=3（米）；（6-1）×0.5=2.5（米）。

师：这两种方法有相同的地方，都用乘法算总长度，区别在于要不要“减1”，你认为哪一种解答是合理的？为什么？

生：我赞同后面一种，这是“两端都种”的情况，棵数比间隔数多1，把人看作棵数，所以要先“减1”，算出间隔数。

生：我也赞同后一种，排队是“两端都种”的情况，我通过画图知道了6名同学只有5个间隔，所以是“6-1”。

师：不错，画图确实可以帮助我们分析问题。我们连起来看这3道题目。第（1）题求的是棵数，第（2）题求的是每个间隔的长度，第（3）题求的是总长度，不管哪一种解答，我们都得先确定什么？

生：都要先确定段数。第（1）题30÷6先算段数，第（2）题从5盏路灯想到5段，第（3）题由6个人排队想到有5个间隔，也就是5段。

师（小结）：是的，“植树问题”从线段图上看，实际上就是研究平均分的问题，以前我们研究了线段图上平均分的“段数”问题，今天我们研究线段图上的“点数”问题。

【思考】从找原型到辨类别，再到题组的比较练习，逐层推进，不断丰富对“植树问题”的整体感知，在变中求同，着力培养学生解决问题的能力与推理意识。最后，通过对题组解答过程的对比，明确把握段数是解答“植树问题”的关键，并由此完善学生对于平均分的学习体验。

（作者单位：浙江省绍兴市柯桥区教师发展中心）