从“学以致用”到“用以致学”

在观察自然现象和科学实验的过程中，经常会遇到两种不同的量：一种量在某一过程中保持固定的数值不变，称为常量；另外一种量在某一过程中可以取不同的数值，称为变量。正比例是刻画某一现实背景中两种相关联的量的变化规律的数学模型，从常量到变量是学生认识水平的一次重大飞跃。虽然学生学习过用字母表示数，对变量有一些感性认识，但是能用函数的观念探索两种相关联的量的变化规律是从学习这个正比例概念开始的。通过这里的学习可以帮助学生进一步加深对数量关系的理解，学会从变量的角度认识两种量之间的关系，初步感受和体悟函数思想。

“认识正比例的量”是苏教版小学数学教材六年级下册的教学内容，本课的教学目标有以下几个方面：1.理解正比例的意义，掌握正比例的字母表达式，会正确判断两个量是不是成正比例关系，能找出生活中成正比例关系的量的实例；2.在具体的生活情境中，经历观察、比较、归纳的学习过程，学会在生活中体验知识，运用知识，感受数学和生活的密切联系；3.渗透函数思想，初步建立事物是相互联系的辩证观念。教学重点是逐步建构正比例的意义，教学难点是引导学生通过观察、思考发现两种相关联的量的变化规律，灵活选择适合的方式去判断两个量是否成正比例关系。

一、问题引入：认识相关联的量

教师出示“风吹草动”这个成语，引导学生思考它的意思。

思考：这里的“风”与“草”，谁主动，谁被动。

提问：生活中还有类似这样“一个事物的变化引起另一个事物变化”的现象吗？让学生结合自己的经验去思考。

学生玩“石头、剪刀、布”的游戏，赢一次加5分，记录一人的得分（平局不算）。

提问：在研究两个数量关系的时候，有没有类似这样“一个数量的变化引起另一个数量变化”的情况？

活动：两个学生猜拳，记录猜拳次数与其中一个学生的得分。

讨论：游戏的次数与游戏的得分是相关联的量吗？

【说明】从学生熟悉的成语、游戏等出发，教师引导学生借助已有经验理解相关联的意思。成语“风吹草动”揭示的是两个事物的相互关联，游戏“石头、剪刀、布”则进一步聚焦两个数量的相关联关系。

二、问题探究：理解正比例的意义

1.问题原型

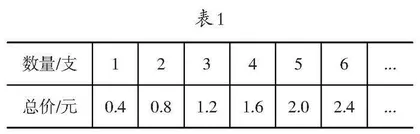
铅笔的数量和总价如表1。

观察：发现两个数量之间的关系及数量变化情况。

讨论：哪个量引起哪个量的变化？两个量分别是怎样变化的？

揭示：如果像表1中数量和总价这样两个量的关系，我们就称之为成正比例关系。

【说明】教师呈现一个正比例关系的典型范例，让学生直观感知两个数量之间的关系。这里教师引导学生讨论，但暂且不做深度追问。初步感知是为下面的深度探究做铺垫的，因为人既不可能探究自己完全知道的东西，也不可能探究自己完全不知道的东西，探究常常发生在“知与不知之间”。

2.问题变式

（1）小明带50元钱上街买东西，用去的钱和剩下的钱如表2所示。

讨论：表2中的两个量成正比例关系吗？

揭示：两个量是相关联的量，但不成正比例关系，因为一个量在增加，另一个量在减少。

（2）用60元去购买笔记本，购买笔记本的数量和单价如表3所示。

讨论：表3中的两个量成正比例关系吗？

揭示：两个量是相关联的量，但不成正比例关系，因为一个量在增加，另一个量在减少。

（3）汽车在公路上行驶，行驶的时间和路程如表4所示。

讨论：表4中的两个量成正比例关系吗？

揭示：两个量是相关联的量，成正比例关系，因为一个量在增加，另一个量也随着增加，且增加得“很匀称”。

（4）正方形的边长和面积如表5所示。

讨论：表5中的两个量成正比例关系吗？

揭示：两个量是相关联的量，不成正比例关系，因为一个量在增加，另一个量也随着增加，但是增加得“不匀称”。

【说明】这里将四组素材逐一进行对比分析，从而加强学生对正比例关系的理解。虽然没有明确揭示概念，也没有呈现图像，但是正比例关系相关的要素都蕴含在讨论过程中。

3.问题模型

讨论：到底什么样的两个量才能称为成正比例关系？

板书：相互关联、同向增减、比值一定。

揭示：如果用x和y分别表示两种相关联的量，用k表示它们的比值，正比例关系可以用下面的式子表示：[y/x]=k（一定）。

练习：如果用a和b分别表示两种相关联的量，

（1）如果a+b=100，那么a、b成正比例关系吗？

（不成正比例）

（2）如果a-b=100，那么a、b成正比例关系吗？

（不成正比例）

（3）如果a×b=100，那么a、b成正比例关系吗？

（不成正比例）

（4）如果a÷b=100，那么a、b成正比例关系吗？

（成正比例）

（5）如果a=100b，那么a、b成正比例关系吗？

（成正比例）

【说明】通过对正比例关系的理解，梳理出判断两个量是否成正比例关系的三个关键。在判断分析的过程中我们要意识到，这里的“相互关联、同向增减、比值一定”是逐步递进的。后面的一组判断题，既是对比值一定的强化，又是对表达不同数量的字母选择的多样性、比值一定的表达式的灵活性的补充说明。

三、问题深化：辨析两个量的关系

1.父亲在29岁时生了小虎，父亲年龄与小虎体重变化情况如表6所示。

揭示：两个量不成正比例关系，因为两个量不是相关联的量，不需要进一步考虑有关比值的问题，就可以直接判断。

2.小虎非常喜欢学习，他开始写字了，小虎写字情况统计表如表7所示。

揭示：两个量成正比例关系，因为两个量是相关联的量（相互关联），一个量在增加，另一个量也随着增加（同向增减），且两个量的比值一定（比值一定）。

3.有一天父亲带小虎上菜市场买菜，为了培养小虎的动手能力，他带了一个弹簧秤（最大质量10千克）。弹簧秤的长度与所挂物体质量之间的关系如表8所示。

揭示：物体的质量与弹簧的长度不成正比例关系，虽然两个量是相关联的量（相互关联），一个量在增加另一个量也随着增加（同向增减），但是两个量的比值不确定。

弹簧伸长的长度与所挂物体的质量之间的关系如表9所示。

揭示：物体的质量与弹簧伸长的长度成正比例关系，因为两个量是相关联的量（相互关联），一个量在增加另一个量也随着增加（同向增减），且两个量的比值一定（比值一定）。

【说明】教师引导学生学会用刚才梳理的“相互关联、同向增减、比值一定”十二字方略，去判断两个量是否成正比例关系，从而强化认识。既加深了学生对概念内涵的理解，同时也为他们学习正比例函数的图像积累了丰富的直观经验。最后一个弹簧秤的例子，通过不成正比例关系的两个量，发现背后蕴含的成正比例关系，进一步加深学生对正比例概念本质的认识。

四、问题拓展：学会用数学思维思考

1.提问：在生活中，你还在哪里看到过成正比例关系的量？

补充：我国国旗的通用尺度定为如下五种规格，具体尺寸如表10所示。

揭示：国旗的大小不一样，但是样子一样，本质上因为这里长与宽是成正比例关系的。

2.提问：其实，两个量之间的关系不仅有正比例关系，还有反比例关系，你能大胆地猜测一下什么样的两个量之间的关系我们称之为反比例关系？

讨论：相互关联、逆向增减……

揭示：其实，我们前面已经见到过成反比例关系的两个量。

延伸：到底什么样的两个量是成反比例关系的，课后大家继续思考。

【说明】如果说，用含有字母的式子表示正比例关系是尝试“用数学的语言去表达现实世界”。那么，分析国旗长与宽的关系中的“变与不变”，就是努力学会“用数学的眼光去观察现实世界”；由正比例类推出反比例的意义，就是努力学会“用数学的思维去思考现实世界”。

五、教学反思

如果要用简练的语言概括本节课教学的一个基本特点，那就是让学生的数学学习从“学以致用”走向“用以致学”。数学教学常常是带着“学以致用”的指导思想来实施的，努力用尽可能短的时间将学生“教会”，然后留出尽可能多的时间让学生来操练，从而逐渐达到熟练的程度。本课的教学，教师没有急于告诉学生正确的概念，而是让学生带着自己粗浅的认识开始尝试应用，鼓励学生在尝试应用的过程中解决问题，通过对问题的反思逐步加深认识，实现对概念的深度理解。这种教学策略，也可以称之为“以用带学”。“以用带学”让认识的提升成为一种拾级而上的自主建构过程。

1.从“理论上懂”到“直观上明”

对概念的理解，不能停留在理论上知道，重要的是要理解其内涵。一首古诗或一篇古文暂时不理解，可以先背诵，然后慢慢消化。但是数学学习，不能不求甚解满足于记忆，更不能沦落为死记硬背。对正比例关系的认识，有些学生学习的结果停留会背诵“十二字方略”。随机调查一些学生，怎样判断两个量是否成正比例关系，他们首先想到的就是做除法、算比值。倘若这样，“理解正比例的意义”这个教学目标就不能真正实现。对于概念的理解，不能停留在表面，而要从本质出发。

2.从“举一反三”到“举三反一”

在概念教学过程中，我们常常喜欢举一个例子来充分讲解概念，然后就问学生理解了没有。倘若学生还有疑问，我们会继续讲解，直至学生认为理解了，我们就觉得新授课的任务结束了。接下来，就让学生去应用概念，去“举一反三”。其实，这样的“举一反三”更多还是在模仿层面。概念教学要在理解上多下功夫，不能用一个简单的例子仓促地呈现结论。概念的建立要尽可能提供相对充分的材料支撑，不能依靠简单说教。教学不能奢求一蹴而就，而要循序渐进，在逐步推进中建构概念，抽象出数学模型。这种逐次推进的策略能充分暴露学生理解中的困惑点，让问题的突破成为一种有层次推进的过程。

3.从“聚焦课时”到“关注整体”

过去，我们的教学常常聚焦在教学目标上，这是基本要求。但是好的教学更要有一种整体思维，将教学聚焦在一种整体性、结构化的视野之中。一个单元的内容本身有着千丝万缕的联系，有些内容的学习需要依赖前摄知识的加持，有些内容的学习能够为后续内容的学习提供支撑。有些内容本身与相关的内容联系极其紧密，只是因为课时的限制才做切割。在教学中，我们可以根据教学内容的特点和班级学生的实际情况适当整合相关内容，注意“瞻前顾后”，实现整体建构。例如，正比例的概念理解与下一课时的正比例函数图像本质上是完全一致、互为补充的；接下来将要学习的反比例与现在学习的正比例是既有联系又有区别的，在学法上也是相通的。所以，在教学过程中，教师要注意整合相关内容，实现相互照应、彼此融通。

总之，儿童学习数学不仅是为了获取知识，还要在获取知识的过程中提升素养、增长见识。学生不仅要学会分析问题、解决问题，还要能够自主地发现问题、提出问题，从而实现从浅层学习向深层学习、迁移学习的跃迁。在教学中，教师要引导学生经历观察、猜测、归纳、计算、推理、验证的具体活动，充分暴露学生的思维过程，直面学生的认知冲突，更好地完成学科育人的根本任务，为学生的全面发展、可持续发展奠定基础。

（作者单位：江苏省南京市瑞金路小学）

本文系江苏省教育科学“十三五”规划重点资助课题“指向教师专业发展的小学数学问题驱动式教学的实践研究”（课题编号：J-a/2020/01）的阶段性研究成果。