整体建构 简教深思

《义务教育数学课程标准（2022年版）》强调，教师要整体把握教学内容，注重教学内容的结构化。教材是落实教学目标、发展学生核心素养的载体。在教学中，教师要重视对教材内容的整体分析，帮助学生建立能体现数学学科本质、对学生未来学习有支撑意义的结构化数学知识体系。基于小学数学单元整体教学的意义，笔者以人教版小学数学教材五年级上册“小数除法”教学为例，深入研究小学数学单元整体教学策略，并提出有效建议，旨在为教师进行单元整体教学实践提供思路。

一、缘起：为何小数除法难教难学

时常听到有教师感叹甚至抱怨，五年级数学最难教，知识点繁多且抽象难懂，尤其是“小数除法”这一单元。笔者深入分析学生作业错因后发现，学生主要错因是：在小数除法的竖式计算时不能理解每一步除的意义，不能利用商不变的性质将小数转化成整数进行计算等。很多教师在教学中将知识点脱离知识整体结构，呈现的是碎片化教学，主要是侧重于对某一节课的研究，缺乏整体性教学设计与教学实践，未能抓住数学知识本质和问题症结，课堂教学存在“只见树木，不见森林”的情况，这些是学生无法掌握“小数除法”知识的重要原因。为此，笔者进行了相关理论分析与实践探究。

二、单元整体教学的实践与探索

在教学中，笔者对“小数除法”单元进行整体设计，主要探究并解决以下三个问题：如何对单元教材内容进行结构化分析？在单元整体教学中，如何让学生达到知识的融会贯通，实现单元整体建构，促进知识的理解迁移？如何培养学生的运算能力、应用意识和推理意识？针对以上三个问题，笔者从学情出发，立足单元核心问题，对本单元教学内容进行整体建构。

（一）厘清知识脉络，对教材进行结构化解读

1.大单元纵向教材分析

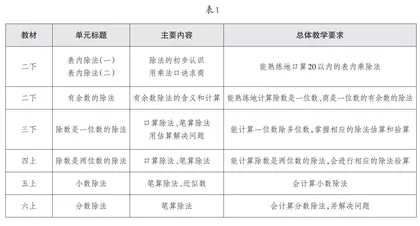
“小数除法”是人教版小学数学教材五年级上册第三单元的教学内容，是“数与代数”领域的重要内容。在人教版小学数学教材中，有关“除法运算”从二年级下册（简称“二下”）开始依次编排了如表1所示的教学内容。

将“小数除法”单元知识置于整个知识体系中进行考量，我们不难发现，“除数是一（两）位数的除法”在整个知识体系中处于核心地位，“小数除法”的算法都是从“除数是一（两）位数的除法”中迁移而来的，其算理也可以用“除数是一（两）位数的除法”的算理和小数的意义来解释。“除数是一（两）位数的除法”的计算方法是从“表内除法”和“有余数的除法”进化而来的。因此，“表内除法”和“有余数的除法”是整个知识体系的基础（如图1）。

整数除法、小数除法及分数除法都是计数单位除以计数单位，计数单位的个数除以计数单位的个数。在教学“小数除法”这一内容时，教师必须让学生感悟小数除法与整数除法运算的一致性。

2.大单元横向教材分析

“小数除法”这一单元共有六个教学板块（如图2）。我们对本单元知识点进行分析整理后发现，“除数是整数的小数除法”是“小数除法”的初步模型，可以为后面学习用转化的数学思想将小数除法转化为整数除法做好铺垫。“一个数除以小数”其实是“除数是整数的小数除法”的变式，其他知识都是围绕这两种小数除法的模型展开并逐步深入，且每个知识点都是相互联系的。

由此分析，这个单元内容大致分为两个板块，例1至例5是计算教学板块，也就是掌握小数除法的算理与算法。例6至例10是小数除法商的处理与生活应用的探究板块。

（二）单元整体建构，促进知识理解迁移

我们发现，人教版教材在“小数除法”的编排上是逐步推进的，让学生掌握小数除法的相关知识，例题较多，不利于学生进行整体性学习。教师有结构地教，学生才能实现有结构地学。本着归类统整的单元整体教学思路，笔者尝试调整相关例题顺序进行整合；将例1至例3整合为一课时，把除数是整数的小数除法算理迁移到整数除法进行教学，感受除法运算的一致性；把例4、例5进行整合，以小数除以小数为典型例题，对小数除法依据商不变性质突出转化思想，提炼出小数除法的算法。为了让学生理解算理、掌握算法，在例题教学后，教师可以根据学生对知识技能的掌握情况，安排相应的计算练习课。

人教版教材在二年级下册“有余数除法”单元中的例5“至少准备几个盒子”就有“进一法”和“去尾法”的内容渗透，三、四年级学习“除数是一（两）位数的整数除法”单元的“问题解决”中也有四舍五入的相关例题学习。基于此，对于例6至例10关于商的处理与生活应用探究板块，笔者将它们整合为“商的处理”进行教学，让学生利用生活情境，感受数学在生活中的运用，如计算钱数时可以精确到角、分，保留一位小数或两位小数。例7至例9侧重商的规律探究，可以整合为“商的神奇”，让学生感受到商的神奇性、商的多样性（如表2）。

（三）聚焦关键课例，突破单元关键知识的理解

1.感悟除法运算的一致性

“除数是整数的小数除法”作为“小数除法”单元的起始课，是沟通小数除法和整数除法的桥梁。它作为本单元的种子课，是基于整数除法，在小数意义、小数计数单位、明晰小数部分“除”的道理和方法基础上进行学习的。

在教学中，结合生活情境“22元买了4个笔袋，平均每个笔袋多少钱”学生能很快用整数除法进行计算，利用“能不能继续往下除”“余下的1元怎么平均分”的问题，学生充分调动已有经验，初步感知算理。在这基础上，教师可以设计关键活动：“写一写，可以用画图、算式、竖式等方法来记录分的过程，再说一说对比整数除法和小数除法，你发现了什么？”

学生能理解十进制“元、角、分”的表征形象，但对算理的理解还需要形成一般表征的抽象过程。在教学中，教师用小数的意义来突出算理“有余数1”也就是10个0.1，进而明确要拆成10个0.1再平均分成5份，从而得到5.2元，再帮助学生理解“点小数点的位置”的方法。此教学环节关于“能不能继续往下除”的问题很好地激发学生思考问题，促进知识的正向迁移，让前后知识能够自然衔接。

教师继而组织学生在小组内尝试解决“王鹏和爷爷应跑多少千米”的数学问题，学生自主探究除数是整数的小数除法该怎么计算，面对“22.4÷4”这个被除数是小数该怎么除的问题，教师可以进行如下教学 。

（1）把千米转化成米，被除数转化成整数。22.4 km=22400 m，22400 m÷4=5600 m=5.6 km。

（2）进行22.4÷4竖式计算（如图3）。

（3）带上小数点进行22.4÷4竖式计算（如图4）。

在教学中，教师要引导学生深入理解小数除法计算的本质，让学生在小数除法和整数除法之间建立联系，让学生的已有经验顺利迁移，理解竖式计算时每一步的意义，理解商的小数点为什么要和被除数的小数点对齐。学生在自主探究“28÷16”时，教师要引导学生再次结合小数的意义说明“为什么添0继续除后，商要写在十分位上”，学生进而总结小数除以整数的计算方法以及要注意的地方。

2.在转化中连通知识

教材中例4、例5的教学是本单元的第二个关键课例，是有关除数是小数的除法转化的问题。学生在学习小数乘法单元时已经有运用转化思想的经验基础。本课主要将学过的知识迁移到新知识的学习中，让学生在转化中感受到这些知识其实是互相连通的。在教学中，教师先组织学生围绕“‘7.65÷0.85’与我们学过的小数除法有什么不同”这一问题展开自主探究、交流，然后学生在不同解题思路的基础上提炼方法，将除数是小数的小数除法转化为除数是整数的小数除法再进行计算，即利用商不变的性质进行计算。“7.65÷0.85”可以把除数0.85转化为整数，0.85的小数点向右移动两位即扩大到它的100倍，同时被除数7.65也要扩大到它的100倍，再根据除数是整数的小数除法算法进行计算（如图5）。

学生再自主尝试计算“12.6÷0.28”，在对比中突出统整后的两个例题的一致性，都是要转化成除数是整数而商不变的算式，进而理解小数除以小数的算理和计算方法。

经过整体建构的单元教学能丰富课堂教学内容，使学生顺利建构知识体系，增强学习体验，强化自主学习能力，从而达到简教深思的教学效果，培养学生的数学核心素养。

（作者单位：江西省安远县思源实验学校）