推理意识的主要表现与任务设计

推理意识是基于特定的数学活动形成的。关于推理意识，《义务教育数学课程标准（2022年版）》在学段目标中给出了较为具体的描述。其刻画了推理意识的三个表现特征，分别是获得猜想、科学验证和合理应用。以此作为推理意识评价的三个维度，形成一级指标，依据相应含义分别细化出两个维度的二级指标：“获得猜想”细化为信息的筛选和联结、猜想的形成与表达；“科学验证”细化为例证的自主与多元、说理的规范与科学；“合理应用”细化为规律的内延与建模、概念的外延与推广。笔者以人教版小学数学教材六年级下册“等量代换”为例，进一步阐述推理意识评价维度与指标在具体内容中的表现及对应任务的设计与实施。

一、素养目标分析与主要表现

教材中的例题包含了两个分别指向图形角度计算和代数运算等量代换的例子。对于命题，学生获得猜想不难，重要的是引导学生通过观察，找到等式中的“关键”，建立相等关系，有理有据地展开演绎推理。

1.获得猜想，培养推理的数学眼光

在推理活动中，猜想是关键和核心。学生能否给出合理的猜想，是学生对题目信息获取、加工、归纳、输出水平的综合表现。根据信息“○+★=160，◎+★=160”，大多数学生认同“○=◎”。但需要进一步通过“写理”任务了解学生处理信息的水平：水平0，直觉或随大流；水平1，关注到等式中相同元素；水平2，依据相同元素能建立起新的相等关系。由于该内容已经给出了可能性结论，在猜想的形成和表达这一指标上的体现较少，重点放在对结论的论证上。

2.科学验证，形成推理的数学语言

验证是指以数学事实为依据，运用数学语言有根据、有逻辑地解释结论和确认结论的形成过程，是例证和说理的综合运用。通过例证说明结论是否正确是数学中常用的验证方式。可能有3层水平：水平0，想不到赋值举例；水平1，举1个例子就说明相等；水平2，举2个或以上例子说明相等。可通过作品解读、对比任务来引发学生对例证数量、形式的积累。学生还需要有能够用简洁、完整的语言有理有据地说明结论的能力。然而，受思维定式、话语系统不完整等因素的影响，说理水平差异明显：水平0，讲不清；水平1，能说清过程；水平2，能联系已有知识进行阐释。教师可以设计“写理、辩理、说理”学习任务，放大演绎推理的流程和依据。

3.合理应用，发展推理的数学思维

在推理过程中，学生自觉调用原有经验主动扩展，择优验证，是推理意识达到新高度的标志。验证时，不论是给“★”赋值，或是借“★”“160”建立新的相等关系，本质就是找到某一个“关键”，实现等式的传递。会有这样几个水平：水平0，无法建立关联；水平1，能感知到论证的过程和依据相似；水平3，明确都存在建立相等关系的“关键”。教师可以通过设计多种验证方式对比任务，明晰等量代换的数学特征和本质。学生面对新的情境时，也能够自觉调用已有经验。会有这样几个水平：水平0，无法建立关联；水平1，有猜想，能验证，但不能完全关联；水平2，关联融通，将新情境的猜想、验证，纳入同一原理体系。概念的外延过程就是类比推理的过程，课堂上可以设计“类比”任务，提升知识应用广度，提高学生的自主调用水平。

二、任务设计与教学实施

根据前期核心素养表现分析以及水平划分，以大多数学生的整体表现水平为基础，笔者设计了“故事中看相等”“问题中写相等”两个猜想任务、“作品中说相等”“对比中悟相等”两个验证任务和“新情境用相等”的应用任务。

1.获得猜想，把“看得见”的相等说出来

任务一：讲故事，看见相等的原因，激活经验。

故事：曹冲称象。

师：谁使大象和石头建立起了相等的关系？

任务二：猜结果，写出相等的原因，图文描述。

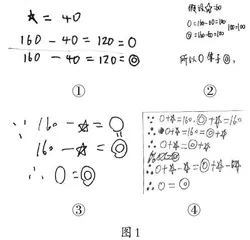
师：如图1，它们相等吗？请你写一写、画一画，用喜欢的方式来说明○=◎。

2.科学验证，把“写出来”的相等说明白

任务三：验证猜想，说出相等的原因，表达认知。

师：作品①、②运用了假设法。

师：作品①中减法算式如何得到？为什么可以用减法？为什么○和◎就相等了？

师（小结）：因为120，它就像一座桥梁，使○=◎，我们把它叫作等式的传递性。

师：作品②中，谁使○和◎建立了相等的关系？

师（追问）：他们都在假设★是多少，为什么不假设○或◎？

任务四：看方法，评价相等的过程，规范说理。

作品③是以“160-★”建立相等关系。

师：能看懂是怎么证明的吗？有什么想要问的？

生：作品④是以“160”建立相等关系的。

师：你能完整解读这个同学的推理过程吗？

师（追问）：这里谁是相等的量，使这两个式子建立了相等的关系？

3.合理应用，把“说清楚”的相等悟透彻

任务五：利用比较法，对比相等的过程，提炼建模。

师：这么多不同的方法都说明了○=◎，这些方法的说理过程有什么相同和不同的地方？

师（小结）：虽然相等的量不同，但都把相等的关系传递了，都有理有据地进行说明。

任务六：换情境，延伸说理的方法，悟透本质。

师：推理不仅存在于运算中，也存在于图形中。如图2，小红说图中的∠1=∠3，你同意吗？请说明。

师：对于这幅作品，你有什么想说的吗？

师（小结）：在推理过程中，我们既要能从条件中看出结论，也可以根据结论去寻找条件。

从故事情境中“船上的记号”，到问题引导“自主写理”，激活学生对相等关系的原有经验；再到“假设具体数值”，用“★” “160－★”或“160”展开说理和提炼，学生对“根据相等的量建立等式”有了更多元、数学化的理解；将推理经验延伸到新情境中，对比关联，学生在“异”“同”中，明晰有理有据的推理过程。

三、素养进阶测评与分析

1.推理素养命题

如图3，现有4个不同的三角形，分别把三角形ABC的边BC延长到点D。

（1）请分别计算∠2的度数，说说∠1、∠2与∠4有什么关系？

（2）它们为什么会有这样的关系？

（3）找一找，还能在图中找到类似相等关系的外角吗？

2.水平层次划分

题目设计了3个小题，分别指向猜想、验证和应用三个指标。首先是计算4个∠2的度数，感知3个度数之间的关系，提出猜想；再引导学生运用所学知识有理有据地说明为什么∠1+∠2=∠4；通过进一步寻找图形中同类相等关系，经历概念内延，完整得到三角形内外角的一般关系，如表1所示。

3.样本数据分析

本次测试一共收集了55份学生样本，根据答题表现，结论如下。

（1）学生能够较完整地呈现推理过程。83.6%的学生会有意识地尝试找条件、写依据、给结论，进行数学化推理说明。

（2）猜想是推理最重要的环节。16.4%的学生的猜想仍处于较低水平，他们的信息调用、关联水平较低，需在课堂上逐步实现推理意识经验的积累。

（3）直觉猜想和数学猜想之间仍有距离。仅有27.3%的学生能找全所有内角和以及与其关联的外角。

四、教学建议

1.完善认知，立足“需求”，激活推理意识

从需求着手，完善认知。一是用好“为什么”，○和◎为什么相等？为什么可以用减法？用学生看似简单的问题，激发学生验证的欲望，激起他们用数学原理解释现象的需求，让学生感受数学间的逻辑关系，使他们停留在直觉层面的认知逐渐走向理性；二是用好“怎么样”，大多数学生都满足于用单一方式进行验证，用“怎么样”解读多种作品，能很好地帮助学生从单点认知走向多点认知，学生会有“原来还可以这样”的感叹；三是用好“怎么办”，演绎推理并非只存在于运算推理中，从任务五到任务六，你会“怎么办”，这是对推理过程的再梳理，也是促使学生对推理的概念学习从关联结构认识到抽象拓展认知发展，打通数学的知识体系与脉络，进一步完善数学知识体系。

2.充分经历，立足“过程”，训练推理方法

推理需要方法的支持，需要经历和积累。一是经历“情境猜想—问题猜想”的过程，情境和问题是激活猜想的两个关键要素，问题更为抽象一些，从“曹冲称象”的情境到“○和◎是否相等”的问题，努力使“记号”与“相同的量”形成支持；二是经历“写理—说理”的过程，这是推理表达的内化过程，任务3中的写理到任务4、5中的说理，学生在从扶到放的过程中，逐步形成规范说理的基本方法；三是经历“合情推理—演绎推理”的过程，同一节课或同一个推理活动，可以有多种不同推理路径，举例验证是大多数学生的选择，是不完全归纳的典型形式，寻找相等量展开验证则是演绎推理的路径，学生在提问、补充中比较不同推理路径的优劣，促进合情推理和演绎推理的融合共进。

3.适时打破，立足“内化”，形成推理思维

“无破不立”，教师要突破形式，帮助学生建立新的认知，发展思维。一破，从一种方法到多种方法，要从多元的作品呈现中感悟不同水平层次的学生思维，感悟解决问题的策略的多样性；二破，从多种方法到统一本质，多种方法的感知，为的是引导学生更好地感受到它们都是从条件、依据、结论进行验证的，而且都是找到了相等的量，为后续学习推理打下理论基础；三破，在数学教学中，推理涵盖所有内容板块，学生常常难以调用如等式性质、运算性质、平角定义等性质、公理论证，教师要有意识地给予学生更多的思考空间，让学生在思考、探讨、辨析中，培养解决数学问题的意识，发展数学思维。

（作者单位：浙江省宁波市奉化区实验小学 浙江省宁波市奉化区莼湖街道中心小学）