指向运算能力发展的表现性任务设计与实施

如何设计并实施表现性任务是发展学生核心素养的关键。刘加霞认为20以内数的加减法口算是培养学生运算能力的根本，其他“十进制数”的计算都可转化为20以内数的加减法口算。因此，“20以内的进位加法”单元教学具有重要价值。本文以此单元为例，依托“‘学-教-评’一致性”实践框架，探析通过表现性任务的设计与实施促进学生运算能力发展的策略。

一、明晰核心素养内涵，确定表现性目标

素养目标及其行为表现是设计表现性任务的出发点和归宿。制订素养目标需要整体把握单元内容的编排逻辑，厘清核心素养的内涵。

上述单元包括“20以内的进位加法算理”和“运用进位加法解决实际问题”两个板块，涉及《9加几》《8、7、6加几》《5、4、3、2加几》三部分内容。《9加几》的教学强调运用凑十法将其转化为“10加几”计算，这样的计算经验可以迁移到其他几部分内容的学习中。凑十的过程就是将计数单位“一”累加到10从而进位的过程。这个过程蕴含着“满十进一”，产生计数单位“十”，能体现数与运算的一致性。

单元教学对学生运算能力的发展具有重要作用。在2022年版课程标准中，相关的目标要求是“能熟练口算20以内的加法，形成初步的运算能力”；教学提示是“引导学生通过具体操作活动，利用对应的方法理解加法的意义，在教学活动中始终关注学生运算能力的形成和发展”；学业质量标准是“能结合具体情境，进行简单的整数运算，形成初步的运算能力”。可见，这个单元对应的主要核心素养是运算能力。2022年版课程标准指出，“运算能力”主要指“根据法则和运算律进行正确运算的能力”。“20以内的进位加法”单元教学体现的运算能力的内涵主要是“明晰运算对象的意义、理解算理和算法的关系”。

基于以上分析，我们构建指向运算能力的单元表现性目标：通过操作、观察、分析等活动，探索并掌握20以内的进位加法，理解其算理，运用其解决简单的实际问题，发展运算能力。

结合前文关于运算能力的维度及其具体表现的论述，以及“20以内的进位加法”单元教材内容，我们细化上述表现性目标：（1）能解释数的组成，以及具体情境中加法算式的含义是把两个部分合起来（YS-①a、YS-②b）；（2）能结合情境、操作活动等，用自己的方法得到20以内进位加法的结果（YS-②a、YS-②c）；（3）能读懂不同的计算方法，说清楚先算什么、再算什么（YS-②b）；（4）能在不同方法的对比中提炼出基本算法，即计数单位“一”累加的数量超过10的加法可转化为“10加几”计算（YS-④b）；（5）能根据实际情况，灵活选择算法（YS-③a、YS-④a）。

二、确定学习起点，设计表现性任务

1.确定学习起点

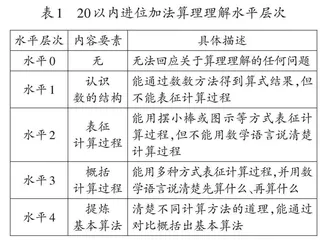
根据细化的表现性目标，我们构建20以内的进位加法算法探索、算理理解的表现性水平层次框架（见表1）。

根据表中内容要素设计前测题，通过前测我们发现，98%的学生能得到9+6的正确结果。其中，32%的学生能用摆小棒、画图的方式表征计算过程，有凑十意识，但不能用数学语言说清楚先算什么、再算什么；12%的学生能用数学语言说清楚先算什么、再算什么。可见，在任务设计中，教师要引导学生先结合真实的问题情境列出进位加法算式，接着借助小棒自主探究算法，并在交流不同算法的过程中感悟凑十法的优势，然后通过圈一圈、说一说，探索如何用枝形图记录凑十的过程；最后解释计算的道理，清楚地表述先算什么、再算什么。

2.设计表现性任务

依据表现性目标、学习起点，教师可以设计低门槛、大空间、多层次的学习任务，帮助学生理解算理、掌握算法。如以下3个课时的8个表现性任务。

表现性任务1“一共有几盒酸奶？”引导学生结合放酸奶情境图列出加法算式，借助小棒摆一摆、画一画、写一写，通过数数、计算等方法得到结果，并把计算方法记录下来。

表现性任务2“圈一圈、算一算、说一说”引导学生在学习单（如图1）上先根据算式圈一圈，再说一说计算过程，最后用符号记录凑十后接着数的计算过程。

表现性任务3“圈一圈、算一算、说一说”引导学生在学习单（如图2）上先根据算式圈一圈，再计算，最后写清楚先算“9＋1=10”、再算“10＋4=14”。

9＋5=

表现性任务4“一共有多少个学生？”引导学生借助情境（如图3）列出算式8＋5，说明算式的意思，并用接着数、凑十等方法计算结果，达成借助已有经验自主探究“8加几”计算方法的目标。

表现性任务5“怎样计算7加几、6加几？”引导学生在学习单（如图4）上圈一圈、算一算，并说清楚计算过程，达成自主迁移凑十法的学习经验探索“7加几、6加几”计算方法的目标。

表现性任务6“怎样计算8＋9？”引导学生灵活选择“把8凑成10”“把9凑成10”“交换加数位置”等计算方法，并对多种方法进行关联与比较。

表现性任务7“怎样计算5＋8？”鼓励学生自主选择计算方法，用喜欢的方式表达思考过程，增强推理意识。

表现性任务8“自主命制进位加法口算题并用喜欢的方法算一算”，引导学生自主探究4加几、3加几、2加几的进位加法，正确计算并说清楚计算过程。

以上任务要求学生在学习单上表征计算的道理和方法，为不同层次的学生提供了探究和提升的空间，有利于反映不同学生的思维水平。8个任务各有侧重，依次递进，如在任务1中，学生要先操作小棒，接着说计算方法，感受累加的数量超过10时要先凑十再接着数；在任务2中，学生不必操作实物，而是先在学习单上圈一圈，然后说一说计算过程，最后用符号记录先凑十再接着数的计算过程；而任务3直接给出算式9＋5，让学生先画图表征计算思路，然后写出先算什么、再算什么。任务设计符合学生的认知发展规律，能帮助他们逐步达成学习目标。

三、组织学习方式，实施表现性任务

1.明确表现性任务要求

在解决问题前明确任务要求尤为重要，教师可以先让学生独立阅读信息，提出关于任务表述或要求的疑惑，然后明确接下来要做的事，但在这个过程中，师生不能就解题思路深入探讨。比如，在明确任务1的要求时，学生知道需要操作小棒表示9+4的计算过程和结果即可，至于具体用什么方法完成不需要讨论，因为这要留待学生后续通过独立思考、小组交流、全班交流等方式探究。

2.读懂学生作品，确定反馈策略

表现性任务强调给予学生表征思维过程的机会。由于学生之间的差异客观存在，所以教师要先对多样化的学生作品进行分类和分层，再思考如何反馈。

如在任务1中，学生借助小棒探究9+4的结果时出现两类作品：一类是通过数数得到结果，这类学生结合加法的含义，通过从9往后数4个数得到结果；另一类是结合情境图用凑十法计算，即先凑出10盒，再加上旁边的3盒，就是13盒。显然，直接数的方法水平层次稍低，凑十法水平层次稍高，因为学生只有认识到10个一是1个十，把1个十和几个一合在一起计算会更简便，才会选用凑十法。因此，在反馈时，教师宜先反馈直接数的方法，再反馈凑十法。学生读懂两种方法后，教师再引导学生通过对比体会凑十法的优势，进而掌握凑十法，能让学生更好地达成表现性目标2——用自己的方法得到9+4的结果。

除此之外，对同一类方法，学生有不同形式或层次的表现时，教师可以采用对比呈现的方式反馈。比如，在任务2中，学生已经会用凑十法计算出结果17，但其表现有多种：表现一，只会在图中圈出凑十的过程，得到结果；表现二，不仅能圈出凑十的过程，得到结果，还能清楚地说出圈的过程，但不能用枝形图正确表征计算过程；表现三，能圈出凑十的过程，得到结果，正确表征计算过程，并说清楚先算什么、再算什么。此时，教师可以同时呈现三种表现对应的作品，让学生思考它们有哪些相同点和不同点，在对比中经历“建构反应”：表现一的学生要在会画的基础上说清楚画的过程；表现二的学生要说清楚先算什么、再算什么。这样的反馈方式能帮助学生更好地达成表现性目标3——结合图示说清楚先算什么、再算什么。

教师可以提前预设学生可能的表现，再在教学时根据实际情况调整。读懂学生的作品，确定反馈策略，是教师实施表现性任务的基本功。教师需要更多地关注学生怎样学，思考为什么学生会有这样的表现和迷思、应该给予学生哪些支持等。

3.设计关键问题，促进思维进阶

在用学生的作品作为教学资源推进学习时，教师要设计关键问题，引导不同层次的学生思维进阶。

在任务2的实施中，学生画图表示通过凑十计算9+8的过程后，要用抽象的流程图和符号表征图示所反映的思维过程，教师需要结合关键问题，引导学生将符号表征与图示表征进行转换，理解“9加几”的算理。比如，教师呈现学生写的算式9+1+7=17后追问：“这里的1和7是怎么来的？你能在图中指出来吗？”“为什么要把8分成1和7？”“9和1相加后，接着要和谁相加，为什么？”“9+8的计算方法与以前学习的加法计算方法有什么不同？”问题串可以让学生更好地理解算理。具体来说，“为什么要把8分成1和7？”的问题引导学生结合数的组成解释8可以分成1和7，并关联9和1可以凑成10、10加几就是十几的已有认知解决问题。再如，学生用凑十法计算9+4，9+8，9+3后，教师可以追问：“这几道题的计算有哪些共同之处？”学生会发现：它们的第一个加数都是9，第二个加数都被分成1和几；都是先算9加1等于10，再算10加几得到结果。这样的追问有助于学生概括基本算法，深化算理理解。

同时，关键问题的设计是教师进行教学评估的一种表现，即根据学生不同水平的表现，通过提问引导他们深度思考，在原有思维水平上得到提升。

（作者单位：广东省东莞市松山湖第一小学）

（本文系2022年度广东省教育研究院教育研究基金项目“基于表现性评价的小学数学精准教学实践的研究”的成果。项目编号：GDJY-2022-M-b25）

文字编辑  刘佳