专题复习“教-学-评”一体化教学探析

笔者以九年级数学专题《二次函数的性质及判断》基础性复习为例，对“教-学-评”一体化复习模式展开论述。

一、研读课程标准，明确复习目标

课程标准是开展“教-学-评”一体化复习教学的重要依据。笔者首先从课程标准中提炼出如下关于二次函数的总体学习要求：理解二次函数的概念、性质（开口方向、对称轴、顶点坐标、最值、增减性等）；掌握二次函数的图象特征及其与解析式中各项系数的关系；能够运用二次函数解决实际问题，包括求最值、交点、区间内的取值范围等。基于此，笔者结合学生的知识储备，确定《二次函数的性质及判断》基础性复习的整体目标：培养学生综合运用二次函数的性质，判断或证明关于系数符号、代数式大小、函数值大小等的结论的正确性。

为了更有效地达成整体目标，笔者结合常见考点，如二次函数y=ax2+bx+c图象与系数a，b，c及△=－4ac符号的关系，有关系数a，b，c的特殊代数式的函数值与0的大小比较，抛物线上点的纵坐标大小比较等，制定了以下层次递进的细化目标：①理解二次函数解析式中各项系数的几何意义；②掌握二次函数图象与x轴交点（个数、横坐标）及对应的一元二次方程的根（个数、值）之间的关系；③会判断含a，b，c三个参数的特殊代数式的大小；④会进一步判断含a，b，c中任意两个参数的特殊代数式的大小；⑤会比较函数值的大小。

二、设计评价任务，促进目标达成

“教-学-评”一体化教学设计过程中要贯穿逆向设计思维，首先确定预期学习结果，紧接着确定评价任务，之后设计教学实践活动。结合本课时的整体目标，笔者设计评价任务时主要关注学生的思维活跃度、知识掌握度、问题解决能力。

1.思维活跃度的评价

评价主要聚焦学生的行为表现，观察学生是否积极参与独立思考、小组合作、课堂讨论等研究活动，能否从多个角度提出疑问或做补充，表达自己的独特见解。如在回顾二次函数解析式中各项系数的意义时，观察学生能否快速说出a的符号代表开口方向，b的符号关联于a的符号及对称轴的位置，c代表的是图象与y轴交点的纵坐标。思维活跃度通过小组讨论和记录情况、学生提问和回答情况等进行评价。？？？

2.知识掌握度的评价

评价主要聚焦学生的学习结果，评估学生对本节课所学重点内容的掌握情况。如利用二次函数y=ax2+bx+c的图象的开口方向、对称轴、与x轴交点情况及位置、增减性等性质，结合抛物线上点的坐标、特殊函数值等，判断系数a，b，c的符号以及特殊代数式的取值。知识掌握度通过课堂练习和课后测试等进行评价。

3.问题解决能力的评价

评价主要聚焦学生学习能力的生成，关注学生在面对二次函数相关问题时，能否灵活运用二次函数的图象及性质，确定问题的研究对象，转化问题，并找到有效的解决问题策略；能否总结所用的解题方法，归纳解题技巧。如通过类比判断含a，b，c中任意两个参数的特殊代数式（2a-b   0，3a+c   0，3b+2c     0）大小的方法，得出只含a，b，c中任意一个参数的特殊代数式大小的方法，同时归纳出判断此类结论的核心技巧——消参。问题解决能力通过案例分析、解题过程展示、错误订正等进行评价。

在实施以上评价任务时，教师要善于捕捉时机，有目的地引导学生思考。对于能力比较薄弱的学生，教师要借助鼓励性评价督促他们积极参与，给予其信心。如根据学生的画、说、写等外显行为表现，对照可观测的教学目标，诊断并反馈学生的学习效果。对于表现优秀的学生，教师要及时肯定他们的进步，引导其更深入地思考。

三、聚焦学习活动，实现学、评一体

教师将评价活动嵌入学习理解、自主探究、应用类比等学习活动过程中，有利于达成复习目标，实现学、评一体。下文结合部分教学过程加以说明。

1.探究活动：探究含a，b，c三个参数的特殊代数式的大小

在学生根据图象判断a，b，c及△的符号后，笔者提问：如果把a，b，c“串”起来，如何判断与a，b，c有关代数式的大小呢？接着，笔者出示例1。

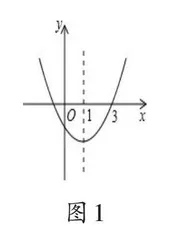
例1 如图1，二次函数y=ax2+bx+c的图象开口向上，对称轴为直线x=1，图象经过（3，0）。完成填空：①a+b+c   0；②a-b+c   0；③4a+2b+c   0；④4a-2b+c   0。

笔者引导学生聚焦共同点观察4个代数式的结构。学生通过对比观察，发现以上代数式都与二次函数解析式的结构相同，均是当自变量取特殊值（如x取±1或±2）时的函数值与0的大小比较，因此得出结论：像这样与二次函数解析式结构相同的代数式，只需根据图象看自变量取特殊值时对应的函数值的正负即可。

在探究活动中，学生通过自主探究，分析特殊代数式的结构，灵活运用抛物线上特殊点的函数值做判断。此外，关于判断含a，b，c三个参数的特殊代数式的大小，师生结合课堂练习共同确定了如下评价标准：一星级，会根据图象上已知点的函数值直接判断；二星级，能熟记常见的特殊结构（与函数值有关）的代数式。

2.类比活动：探究含a，b，c任意两个参数的特殊代数式的大小

除了上述与解析式结构相同的代数式，我们还经常遇到有关a、b、c的其他形式的代数式，笔者出示例2并追问：对于与解析式结构不同的代数式，我们怎样判断其大小呢？

例2  二次函数y=ax2+bx+c（a≠0）的图象如图2。完成填空：①2a-b   0；②3a+c   0；③3b+2c   0。

笔者先引导学生观察这类代数式与例1的不同点。显然，它们的参数从原来的三个变成了两个。笔者提问：怎样减少参数？学生分析图象，不难回答：由对称轴得出a与b的关系，就能用a代替b，或用b代替a，从而减少一个参数。笔者追问：类比例1，怎样判断a与c，b与c之间相关代数式的大小？学生就此问题进行小组合作学习，得出结论：3a+c，3b+2c均与当x取1时的函数值a+b+c有关，只是借助a与b的关系消去了参数a或b。由此，学生归纳出判断a，b，c中任意两个参数大小关系的方法与技巧——消参，缺“谁”消“谁”。

笔者通过解题过程展示、同伴点评及质疑等方式对学生的学习效果进行评价。在展示环节，笔者让学生清晰展示解题步骤，引导他们关注解题思路、方法运用和结果的准确性。在同伴点评及质疑环节，笔者鼓励学生从不同角度，如思路、方法、结果等方面进行点评和质疑。学生的解题展示可以反映他们对知识的掌握和运用情况，同伴点评能促进学生之间相互学习，质疑环节则有助于培养学生的批判性思维。最后，笔者设置学习评价表，让学生对照学习评价表中所列项目，如会识别特殊形式的函数值、会消参、会根据图象找等量关系等，自主反思解题收获，自我评定星级。

（作者单位：武汉市光谷第一初级中学）