图形的运动教学路径探析
作者: 费利平
图形运动的本质是图形上点的位置变化,引导学生用动态视角理解图形的运动是教学的关键。笔者以人教版数学五年级《旋转的再认识》教学为例,探索图形的运动教学路径,借此帮助学生积累关于图形运动的活动经验,深入理解图形运动的特征,增强几何直观和空间观念。
一、启程:素材精选与活动探究
笔者在课前选择三角形、长方形、椭圆等简单图形作为素材,设计关于旋转运动的动画。上课伊始,笔者播放动画,引导学生观察三角形、长方形、椭圆经过多次旋转形成美丽图案的过程,直观感知旋转运动现象,感受数学之美,增强探究旋转运动特征的兴趣。笔者还在课前让学生尝试在方格纸上画出线段AB旋转90°后的图形,并用他们的前测作品作为课堂教学素材。
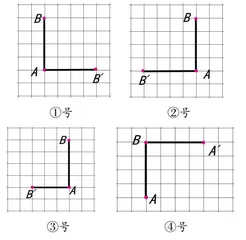
课堂上,笔者呈现如图1所示的旋转方向、旋转中心不同的各类作品,并据此设计与实施以下三个探究活动。
活动一:想一想
笔者先让学生仔细观察这些作品,说一说有什么发现,然后组织学生小组讨论,引导学生汇报、交流。交流中,学生提出③号作品和⑥号作品是错误的,因为旋转后线段的长度与原线段的长度不一致。一名学生认为,只有①号作品和⑤号作品是正确的,其他的都不对,他给出的理由是线段AB只能顺时针旋转。针对这个错误认知,笔者及时纠偏,告诉学生旋转运动有顺时针和逆时针两个方向,②号作品和④号作品是正确的。
活动二:分一分
基于以上认识,笔者让学生将正确的作品分类,并说一说分类标准。在交流过程中,学生发现分类标准不同,分出的结果就不同。具体来说,有的学生以旋转中心分类,把①号作品和②号作品分为一组,④号作品和⑤号作品分为一组;有的学生以旋转方向分类,认为①号作品和⑤号作品都是顺时针旋转90°,②号作品和④号作品都是逆时针旋转90°;还有的学生提出以旋转的角度分类,①号作品和⑤号作品都是顺时针旋转90°,②号作品和④号作品也可看作顺时针旋转270°。笔者点拨:分类的标准涉及旋转中心、旋转方向、旋转角度三个要素,只有把它们都说清楚,我们才能准确判断图形是怎样旋转的。
活动三:说一说
笔者引导学生用旋转中心、旋转角度、旋转方向这三要素规范地描述线段AB旋转的过程。针对①号作品,有的学生描述为“线段AB绕点A顺时针旋转90°”,有的学生描述为“线段AB绕点A逆时针旋转270°”。
本环节以6幅典型作品为学习素材,引导学生通过多种活动方式进行自我构建,经历了从判断正误到明晰旋转三要素,再到准确描述图形旋转的学习过程。
二、深化:问题引领与认知完善
基于学生对旋转三要素的理解,笔者设计了两个追问,引导学生深化对旋转的认知。
问题一:线段只能绕它的两个端点旋转吗?学生很容易想到以线段的中点为旋转中心进行旋转得到的图形,但作图有一定的困难。笔者大胆放手,鼓励学生先用铅笔代表线段进行实物演示,观察铅笔绕其中点顺时针旋转90°前后笔尖等对应点的位置关系,然后想象线段AB绕其中点顺时针旋转90°后的样子,最后在方格纸上画出线段AB旋转后的图形。
问题二:线段除了绕它的端点和中点旋转,还能绕其他点旋转吗?你能试着画一画吗?这个问题具有一定的挑战性和开放性。学生画出的作品除了绕线段上任意一点旋转的情况,还有将旋转中心放在线段外部的情况。最后,笔者用课件演示线段绕有代表性的不同位置的点旋转的过程,引导学生用旋转三要素描述线段的旋转,完善学生对旋转的认知。
三、实践:动静结合与操作理解
教学过程中,笔者在实践环节设计了三个层次的作图活动。
第一层次是线段的旋转,即在方格纸上画出线段AB绕点A或点B旋转180°后的图形。一开始,个别学生提出按什么方向旋转的疑问,笔者告知学生旋转方向自定。后续交流中,学生对比观察作品后发现,只要绕同一个点旋转180°,不管是顺时针旋转还是逆时针旋转,所得图形的位置是一样的。
第二层次是直角三角形的旋转。第一步,笔者出示图2,让学生先想象直角三角形ABC的旋转过程,再在方格纸上借助三角尺动手操作,演示三角形ABC按顺时针或逆时针方向旋转90°,并指名学生在黑板上演示。第二步,笔者引导学生验证,即让学生将旋转后的三角形向反方向旋转90°,看其能否与原图形重合。第三步,笔者用课件动态演示直角三角形ABC旋转时三条边位置的变化情况,有意识地让学生感受直角三角形斜边的旋转过程,并要求学生找出斜边上某个点旋转后的对应点,通过连接相应的点,直观感知三角形的每一条边都是绕旋转中心按顺时针或逆时针方向旋转了90°。第四步,笔者引导学生自主画图,填写“我将直角三角形ABC绕点( )按照( )方向旋转( )度”,并说一说三角形旋转前后的变化情况。
由线段的旋转到三角形的旋转,是由线到面的拓展,有助于学生理解图形旋转前后形状、大小不变,只是位置改变。
第三层次是一般三角形的旋转。这是在学生掌握直角三角形旋转90°的作图方法基础上进行的拓展。学生对比直角三角形斜边的旋转,想象一般三角形旋转前后的位置以及每条边的旋转过程,然后按具体要求在方格纸上画出一般三角形旋转90°后的图形。通过汇报交流,学生得出一般三角形的旋转就是线段的旋转,而线段的旋转其实是线段上点的旋转。
实践环节中,学生经历探索图形旋转的全过程,在动静结合中形成了图形旋转运动的清晰表象,理解了旋转三要素,并在动手操作中感悟到图形运动的本质是图形上点的位置变化。
四、升华:创意设计与拓展应用
数学课程标准提出“能借助方格纸设计简单图案,感受数学美,形成空间观念”的目标要求。为此,笔者设计了拓展学习环节。
旋转现象在生活中很常见,学生并不陌生,笔者先让学生列举生活中的旋转现象,接着用课件出示摩天轮转盘、酒店旋转门等动态图片,以及不同图形多次旋转后的图案,激发学生的创作灵感,然后引导学生灵活运用简单图形的多次旋转创作美丽的图案。有的学生利用三角形的多次旋转创作出美丽的图案(如图3-1),有的学生把花瓣图形不断旋转得到漂亮的花朵(如图3-2)。在变换与重组中,学生进一步理解了图形的旋转,领略到图形的运动之美。
最后,笔者追问:刚才我们都是绕某个点进行图形的旋转,如果图形绕某一条边旋转会是怎样的呢?学生在笔者引导下拿出事先准备的长方形纸、正方形纸或三角尺等学具,让学具沿着它自身的一条边快速转动一周,观察并想象会得到什么图形。经过猜想、动画演示,学生总结得出:长方形绕它的一条边快速旋转可以得到圆柱,三角形绕它的一条边快速旋转可以得到圆锥。这样教学,学生直观感知到平面图形经历旋转运动后得到立体图形的过程,感悟了面动成体,增强了空间观念。
(作者单位:黄石市阳新县富川小学)