《轴对称的再认识》教学思考与实践
作者: 刘元宇
“图形的运动”涉及平移、旋转、轴对称三个核心内容,旨在提升学生的空间观念和几何直观素养。教师采用一致的路径教学“图形的运动”三部分内容,有利于学生掌握研究图形运动的方法,积累研究图形运动的经验,形成整体性认知。笔者以人教版数学四年级《轴对称的再认识》教学为例做具体阐述。
一、化静为动,在操作中感知
日常教学中,我们往往只注重研究静态的轴对称图形的特征,而忽略了轴对称的运动本质。解决这个问题的关键是化静为动,让轴对称“动”起来。
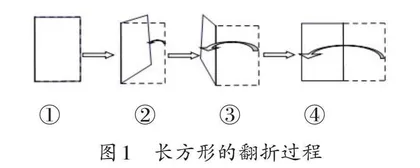
《轴对称的再认识》中,对于如何得到轴对称图形,教材介绍的方法是“对折剪出来”。笔者认为这样的方法有缺陷,因为遇到学习材料不是纸片、不能剪的情况时,学生可能会束手无策。基于此,笔者抓住“如何得到轴对称图形”这一核心问题展开教学,意图改变学生的思维方式,让学生把看待图形运动的视野从平面拓展到空间,理解图形沿着对称轴作180°翻折,翻折前的图形和翻折后的图形组合在一起就得到轴对称图形。课堂上,笔者先让学生用书本演示平移和旋转运动,接着追问:“你会演示轴对称运动吗?” 学生基于之前的学习经验动手对折,认为对折就是轴对称运动。其实,对折只是用来验证一个图形是不是轴对称图形的一种方法。为帮助学生理解轴对称运动的本质,笔者先用课件演示将书的封面抽象成长方形并翻折180°的过程(如图1所示,①是翻折前的图形,②和③是翻折中的样子,④是翻折前和翻折后组成的图形),接着让学生尝试用手中的书操作翻折的过程,直观感知轴对称运动,最后用课件演示几种不同图形的翻折过程,让学生直观感知翻折前的图形和翻折后的图形可以组成一个轴对称图形(如图2)。
二、由点到面,在探究中理解
图形运动的本质是图形上点的位置变化,笔者抓住这一核心知识引导学生以点的位置变化为起点,发散到线段的位置变化以及面的位置变化,让他们的空间观念由点到线、由线到面地逐步增强。
在《轴对称的再认识》教学中,笔者设计了自主探究学习单。活动一要求学生通过数一数、找一找等实践活动,总结出轴对称图形的特征。
1.如图3,数一数,写出对称点到对称轴的距离。
点A到对称轴( )格,点A'到对称轴( )格。
2.找一找,标出对称点,并写出对称点到对称轴的距离。
点( )到对称轴( )格;点( )到对称轴( )格。
点( )到对称轴( )格;点( )到对称轴( )格。
我可以找到( )组这样的对称点。
我发现: 。
学生在探究活动中容易找到图形上线段的端点(关键点)进行研究,可以找到如图4所示对称点B,B'和C,C',也能正确数出点到对称轴的距离。
笔者随机指名学生上台展示自己的探究成果,其他学生补充。随后,笔者追问“到底能找到多少组不同的对称点”,并让学生小组讨论或者独立在学习单上找一找、画一画。学生归纳得出:线段上有无数个点,这些点都可以找到对称点,所以有无数组这样的对称点,并且每组对称点到对称轴的距离都分别相等。然后,笔者引导学生反思这些“容易找到的”对称点有什么共同特点。学生再次深入探究得出:这些“容易找到的”对称点通常是线段的端点,可以称之为图形的关键点;不只是每组关键点到对称轴的距离分别相等,而是图形上所有的对称点到对称轴的距离都分别相等。
学生理清轴对称图形中点与点的关系后,笔者追问:“除了点与点之间有对称关系,你还有什么发现?”有了前面的学习做铺垫,学生能够直观感知到对称轴两边的两个面是对称的,但对于线段的对称,学生不能准确理解,究其原因是学生对点、线、面之间的关系认识不清。为了突破这个难点,笔者先用课件呈现图4中线段BC上的多个点,引导学生思考这些点沿对称轴翻折后的样子,然后演示这些点翻折后形成对应点的过程,并顺次连接这些对应点,得到线段B′C′,让学生直观感受线段BC与线段B′C′对称。类似的,学生不难得出线段AB与线段A′B′也对称,进而理解了点动成线、线动成面,进一步认识到图形运动的本质是图形上所有点的运动。
在活动二中,笔者设计了两道实践操作题,旨在让学生利用轴对称图形的特征,探究补全轴对称图形另一半或画出一个图形经历轴对称运动后形成轴对称图形的方法。
1.如图5,根据已知图形(左右两图任选其一)和对称轴,先想象图形轴对称的过程,再补全另一半。
2.补全后跟同桌说说补全方法,总结怎样画得又好又快。
交流中,学生汇报了两种不同的作图方法:一是先根据左边已知图形的线段画对称线段,再连接线段;二是先找左边已知图形上的关键点(线段的端点),确定对称点,再依次连接这些对称点。笔者引导学生对比两种作图方法,结合自己的实践经验,总结得出“一找(关键点)、二定(对称点)、三连(依次连接对称点)”的作图方法。学生在动手操作中体会到轴对称运动中点动成线、线动成面的过程,深刻理解了图形运动的本质。
三、以学定教,在参与中获得
在学生积累了基本的活动经验,获得了有关轴对称运动特征的认识,掌握了轴对称图形的画法后,笔者设计了一道开放性习题,要求学生在方格纸上画出直角梯形经过轴对称运动后形成的轴对称图形,并标出对称轴。
不同层次的学生会形成不同的作图方法。学生汇报了如下两种方法:一种是分别以直角梯形四条边中的一条为对称轴进行轴对称运动,得到四种不同样态的轴对称图形;另一种是以直角梯形外部的任意一条直线为对称轴进行轴对称运动,形成多种样态的轴对称图形。笔者借助多媒体演示这个直角梯形进行轴对称的过程,让学生直观感知直角梯形左右翻折或上下翻折的运动过程,体会沿着不同的对称轴翻折可以得到不同的轴对称图形。为了发展学生的空间观念,拓展学生的思维,笔者又借助几何画板演示直角梯形以一条边为对称轴进行翻折的过程,让学生在对比观察中感知直角梯形翻折的角度不同(如平角、钝角、直角、锐角),所形成的轴对称图形也不同。这样,学生在动手操作、合作交流、观察想象等参与式学习活动中拓宽了对轴对称的认识,增强了空间想象力。
四、由此及彼,在互动中关联
轴对称现象在生活中很常见,笔者结合中华优秀传统文化,以剪纸为素材创设“喜字变变变”互动游戏,帮助学生巩固对轴对称运动的认识,关联轴对称与平移两种图形的运动。
首先,笔者出示“”剪纸图形,将其轴对称变换(翻折180°)1次,得到一个“喜”字样式的图形,接着将前一次轴对称变换后的图形再次轴对称,以此类推,经过多次轴对称变换,依次形成如下表所示的图形。
笔者引导学生观察剪纸图形翻折的过程并思考有什么发现。学生小组讨论,交流汇报,共同归纳得出:连续轴对称单数次,轴对称后的图形和原图形可以组成一个轴对称图形;连续轴对称双数次,轴对称后的图形和原图形不可以组成一个轴对称图形,但可以看作是原图形向右平移得到的图形。也就是说,图形通过多次轴对称变换,得到的可能是原图形轴对称后的图形,也可能是原图形平移后的图形。这样设计教学巧妙地勾连了轴对称和平移两种图形的运动,让学生认识到它们的共性特征:图形的形状、大小不变,位置变了。
(作者单位:黄石市阳新县富川小学)
责任编辑 刘佳