模型观念：内涵、培养路径及教学示例

【摘 要】培养学生的模型观念是义务教育阶段数学教育的重要目标之一。基于对模型观念的内涵理解，教师可以从以下三个途径优化应用类问题教学：紧贴生活，呈现实际问题的原生性；合作探究，经历数学建模的过程性；分步实施，体悟数学建模的阶段性。

【关键词】初中数学；模型观念；数学学科德育；数学建模能力；应用类问题

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2024）39-0046-05

【作者简介】孙凯，江苏省苏州市阳山实验初级中学校（江苏苏州，215151）教师，高级教师。

数学是一门逻辑性很强的基础科学，也是一种应用广泛的技术。数学应用性的实现途径主要是数学建模。近年来，国际数学教育界越来越重视数学建模，都将培养学生的数学建模能力作为重要内容写入数学课程标准。［1］我国数学教育也尤为注重学生数学建模能力的培养。根据学生的心理特征和认知水平，新的数学课程标准在小学、初中、高中三个学段分别提出了模型意识、模型观念和数学建模的课程目标和教学要求。

为了凸显数学与现实世界的联系，苏科版初中数学教材中设置了大量与生活实际紧密联系的问题情境（尤其在数学概念和数学知识应用的内容部分），但这些问题情境的教学目标单一，问题的数学化程度高，更侧重于建构标准数学模型求解问题，有利于培养学生模型观念的再现水平，在模型观念的联系和反思水平上却表现不足。在实际教学中，我们发现这些问题情境具有简化性、封闭性、确定性等特征，与综合性、开放性、不确定性的数学建模问题相比，这样的问题情境难以驱动学生完整经历数学建模活动过程，培养初中生模型观念的效果不佳。

一、模型观念的内涵

1.对模型观念的理解

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）明确提出，要培养初中生的模型观念。模型观念是指初中生在解决实际问题时，对建立数学模型，求解模型并验证结果，最终阐释实际问题的过程有清晰的认识。具体要求为，“对运用数学模型解决实际问题有清晰的认识，知道数学建模是数学与现实联系的基本途径，初步感知数学建模的基本过程，逐步建立模型观念”［2］。

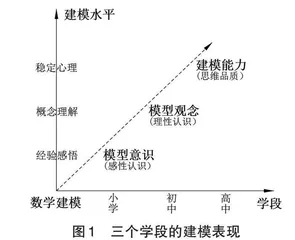
模型观念是一种基于对数学概念的理解，逐步形成的对数学模型特征、问题与思考方式的理性认识；模型意识是一种数学学习经验的积累，是学生在简单数学建模活动中形成的感性认识；建模能力是一种稳定的心理特征，是学生经历数学建模活动，在问题解决的过程中形成的数学能力和思维品质。［2］51小学、初中、高中阶段学生的数学建模表现如图1所示。相较于“数学建模的能力”而言，“模型观念的认识”的要求稍微低一些，这与初中生数学知识和能力水平不高以及掌握的数学模型有限等因素相关。从模型观念的“认识”的内容看，主要包括“运用数学模型”“解决实际问题”两个方面；从“认识”的过程看，主要包括从实际问题中抽象出数学问题，用数学符号建立方程、不等式、函数、统计、概率等数学模型，求解模型获得数学结果，讨论结果的意义并阐释问题。［3］模型观念的功能体现在让学生知道数学建模是联系数学世界与现实世界的基本途径，其意义在于在问题解决的过程中提高数学语言表达能力，感悟数学应用价值。

2.模型观念与数学建模的关系

新课标给出了数学建模的基本过程。研究发现，模型观念下的数学建模基本过程与《普通高中数学课程标准（2017年版2020年修订》（以下简称“高中数学新课标”）中数学建模的过程基本一致，一般将其简称为数学建模五阶段循环模型［4］（如图2），具体包括：从现实原型简化出现实模型（实际模型），从现实模型数学化形成数学模型（数学形式），求解数学模型获得结果，用数学结果解释现实问题，解答并验证现实问题。

模型观念是对数学建模的一种认识，学生的模型观念必然形成于数学建模活动，因此，开展数学建模活动是培养学生模型观念的重要路径。数学建模活动具有现实性、开放性、过程性、阶段性等特征。数学建模的关键环节是“现实原型—实际模型—数学形式”这一子过程。［5］从这个维度看，苏科版初中数学教材上提供的数学概念类问题情境和数学知识应用类问题情境非常适合开展数学建模活动，但这些问题情境削弱甚至缺失了数学建模的简化环节、数学化环节，教师在教学时可根据教学需要对其进行改编和优化。

二、模型观念的培养路径

创设真实、合适的问题情境是培养模型观念的基础，经历数学建模的基本过程是形成模型观念的必经路径。［6］初中代数的许多应用问题具备了数学建模活动的部分特点，有助于学生形成与发展模型观念。［3］80在苏科版初中数学教材中，方程、不等式、函数、统计、概率等内容适合开展数学建模教学活动。从数学建模活动过程看，以现实原型为背景的数学应用类问题（以下简称“应用题”），适合开发和组织数学建模活动。基于对苏科版初中数学教材设置的问题情境的理解和认识，以教材提供的应用题为基础，笔者建议从以下三个途径优化应用题教学，培养学生的模型观念。

1.紧贴生活，呈现实际问题的原生性

原生性是对实际问题属性的一种描述，是指实际问题应源于学生身边熟悉的现实生活现象，不加任何简化、假设和修饰，表现出现实原型的原始样态。原生性的实际问题与传统的应用题相比，具有真实性、综合性、复杂性、开放性、挑战性等特点，在培养学生的数学化能力上具有重要价值。事实上，在现实生活中，我们遇到的绝大多数问题都是“原生态”的。就数学学科而言，往往需要问题解决者会用数学的眼光对实际问题进行观察和抽象，从而转化为数学问题，用数学的语言建立数学模型并求解。因此，在应用题教学中，教师应根据学生的认知水平，以教材上与现实生活紧密联系的应用题为基础，结合真实的现实生活对其加以“回溯”，追根溯源，弱化数据信息，还原真实的问题原型，凸显实际问题的真实性、开放性、原生性，以更“原生”的样态呈现给学生，创设良好的数学建模情境。

2.合作探究，经历数学建模的过程性

原生性的问题情境为学生提供了良好的建模载体，这种问题情境具有综合性、复杂性、开放性、挑战性的特征，适宜使用“自主+合作”探究的学习方式。教学中，教师应注重引导学生独立探究与合作探究相结合，积极参与相对完整的数学建模活动，经历数学建模的过程。数学建模活动一般包括以下几个环节。

（1）简化原生性问题，形成现实原型；

（2）现实模型数学化，建立数学模型；

（3）求解数学模型，获得数学结果；

（4）运用数学结果解释现实原型；

（5）根据验证结果，修正模型。

学生只有经历相对完整的数学建模活动过程，才能从对数学建模的初步感知发展到对数学建模的清晰认识，从而逐步发展模型观念。

3.分层实施，体悟数学建模的阶段性

国内外学者对数学建模内涵的认识是多维度的，比较有代表性的理解有三种：数学建模是一种活动过程，数学建模是一种数学思想，数学建模是一种数学能力。［7］三种理解是学科视点的差异，虽侧重点不同，但没有本质上的差别。基于对高中数学新课标中数学建模的理解，结合新课标中关于“数学建模的基本过程”的分析，笔者将数学建模理解为在数学建模活动过程中培养学生的模型观念。数学建模是一个相对完整的活动过程，在整个过程中大致可以分为五个阶段，每个阶段对模型观念培养的侧重点不同。例如，在将原生性问题（现实原型）简化为现实模型阶段，教学侧重点在于引导学生分析和思考问题的相关影响因素，剔除次要因素，确定主要因素，对原生性问题进行必要的简化、假设、抽象，体会数学建模中简化环节的重要性。又如，在将现实模型数学化建立数学模型阶段，教学侧重点在于培养学生的数学化能力，具体包括关系梳理、主要因素分析、数据收集、主要问题筛选、提出问题、符号表征等。通过数学建模活动阶段性的分步实施，驱动学生体悟建模活动过程，发展模型观念。

三、教学示例

1.教学内容

苏科版初中数学八年级上册第6章第4节“用一次函数解决问题”第1课时。

2.教学目标

（1）能从实际问题中抽象出数学问题，并建立函数模型并求解，在用一次函数表述数量变化及其关系的过程中，发展模型观念；

（2）经历“现实问题—数学问题—建立模型—求解验证”的数学活动过程，积累数学建模活动经验；

（3）在问题的解决过程中，感悟数学的抽象性、严谨性和应用的广泛性，体会数学的应用价值。

3.教学过程

（1）呈现原生问题

【问题情境1】玉龙雪山

踏进丽江，首先映入眼帘的是那拔地而起的巍巍玉龙雪山。玉龙雪山为云南省丽江市境内雪山群，由13座山峰从南向北纵向排列组成，宛如一条“巨龙”腾越。远眺玉龙雪山，能看到一条黑白分明的分界线，人们把它称为“雪线”。雪线以上银装素裹、云雾缭绕，雪线以下山林密布、湖水相依。近年来，很多游客包括丽江本地人都说，玉龙雪山上的雪，远不及以前壮观了。由于气候变暖等原因，玉龙雪山的雪线每年都在上升，这样下去雪线是否会退至山顶而消失？

【教学说明】呈现原生性的问题情境，引导学生用数学的眼光观察现实生活中的问题，从实际问题中抽象出数学问题，建构适切的数学模型并求解，会用求解的数学结果解释实际问题。在这里，将教材上的原问题情境中的数据剔除（主峰海拔5596m，雪线海拔4500m），意在呈现真实问题的现实原型，凸显问题情境的现实性、真实性、开放性，激发学生探究问题的兴趣。

（2）简化现实原型

学生活动预设：小组合作尝试将原生性问题进一步抽象，进行数学化表达，转化为数学问题，制订解决问题的方案。

影响因素预设：全球性气候变暖；冰雪消融量增加，冰雪来源减少；大量游客涌上玉龙雪山与冰川亲密接触，也使得冰川冰雪加快融化。

【教学说明】因原生性问题中没有提供相关数据，学生一开始是茫然的、手足无措的。但随着对影响因素的分析，学生逐步认识到要收集主要影响因素的数据，并对问题进行必要的简化和假设，从现实原型中简化出现实模型，形成数学问题。

（3）建构现实模型

教师提供数据：主峰海拔5596m，雪线海拔4500m，丽江玉龙雪山冰川与环境观测站观测发现2003年至2008年，玉龙雪山雪线上升约50m。

数学问题：玉龙雪山由13座山峰组成，主峰海拔5596m，在海拔4500m处的雪线平均每年上升约10m。假设雪线的高度按此速度不断变化，几年后玉龙雪山的雪线将由现在的海拔4500m退至山顶而消失？

【教学说明】在建构现实模型环节，让学生经历数据收集、抽象、假设等阶段性建模过程，在探究中分析、筛选主要影响因素，确立时间与雪线海拔两个主要因素，为建立数学模型作铺垫。结合主要影响因素的数据信息，进一步对现实模型进行数学化表达，形成清晰的数学问题。

（4）建立数学模型

建构模型：玉龙雪山问题情境中的数学模型具有一定的开放性，预设学生会建构不同的数学模型求解。

活动预设：模型1—算术模型：（5596-4500）/10；模型2—方程模型：设经过x年玉龙雪山的雪线将退至山顶，根据题意，得10x+4500 = 5596（求解略）；模型3—函数模型：设雪线海拔为y（m），时间为x（年），则函数表达式为y=10x+4500。

【教学说明】鼓励学生建立不同的数学模型求解数学问题，体现模型的多样性，引导学生比较不同数学模型的优劣，凸显函数模型的优越性。

（5）求解数学模型（略）

【教学说明】教学中教师还可以根据数学模型的求解结果，实施数学学科德育渗透。例如，建设观测站，修建湿地湖泊群，增加植被覆盖率，增加地表水体，限制旅游人数等。又如，低碳出行，保护水源，节约用水，保护动物等。