新版课标视域下小学数学高阶思维的内涵、价值及培养策略

基金项目：江苏省教育科学“十四五”规划2022年度重点课题“新版课标视域下小学数学高阶思维培养实践研究”（立项号为B/2022/03/215）。

作者简介：孟庆甲（1974—），正高级教师，江苏省小学数学特级教师，全国优秀教师，连云港市教育科学研究所研究员。曾获江苏省“333高层次人才工程”培养对象、省教科研先进教师、省课程改革先进个人、省“杏坛杯”课堂教学展评特等奖等荣誉，先后主持和参与省级课题7项。

［摘  要］ 数学是思维的科学，数学高阶思维能促进学生深刻揭示数学本质属性。基于此，教师应打造充满智慧与思辨的数学课堂，通过深度打磨、不断探索，让高阶思维的触角延伸力更加犀利；通过精心建模、精益求精，让高阶思维的拓展优化力更加灵活；通过情智在场、具身投入，让高阶思维的内在驱动力更加“魔幻”。

［关键词］ 数学高阶思维；内涵；价值；培养策略

数学是思维的科学，它为人们提供了一种理解与解释现实世界的思考方式。毫不夸张地讲，没有思维就没有真正的数学学习，也就无法深入研究数量关系和空间形式。学生只有灵活掌握和运用数学思维，才能不断挖掘自身的数学学习潜能，形成和拥有个性化的数学眼光、数学思维和数学语言。培养和提升学生数学高阶思维力，能真正实现“会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”［１］。实践证明，教师只有打造充满智慧与思辨、灵动与创新的数学课堂，才能引导学生逐步跨越浅表思维、低阶思维，才能真正使学生迷恋数学学习，催生高阶思维、启迪灵动智慧、升华数学思想。

一、新版课标视域下数学高阶思维的内涵

所谓数学高阶思维是指在富有挑战性的数学学习活动中，教师围绕明确的数学学习目标和数学任务，让学生通过观察分析、积极猜设、实践操作、思辨验证，具身经历和体验不断发现问题、提出问题、分析问题与解决问题的探索研究过程，能够灵活运用数学批判性思维、创造性思维解决问题的高层次认知水平的心智活动或认知能力［２］。

由此可以发现：数学高阶思维具有问题性，具备创设情境、巧设问题、驱动引领、追本溯源的功能；数学高阶思维具有深刻性，能够达到聚焦本质、鞭辟入里、逐层推进、透彻深刻的作用；数学高阶思维具有灵活性，能够灵活切入、善于变通、多元思考、举一反三；数学高阶思维具有严谨性，并具有过程严谨、思考全面、有理有据、严丝合缝的特点；数学高阶思维具有批判性，能够促进学生理性面对、敢于质疑、不断反省、审视思辨；数学高阶思维具有独创性，能够促使角度新颖、善于发散、思维独特、追求创新。

二、新版课标视域下数学高阶思维的价值

1. 深刻揭示数学本质，促进思维多元链接、结构生长

数学高阶思维能够促使学生不断深入数学知识内核、问题深处，逐步抽丝剥茧、清晰地把握和揭示数学知识、数学问题的来龙去脉与本质属性，同时不断唤醒和链接直接或间接的数学知识、方法、客观现象、真实情境与自身经验，建立多方、多维、多元的知识逻辑联系、解决问题方法和策略的逻辑联系，建立网络化、立体式的知识结构。

2. 深层依据概念原理，驱动逻辑思维推理、智慧思辨

数学高阶思维能够促使学生精准把握、透彻理解和灵活运用数学概念、定理、法则和公式，依据数学事实、生活实际、内在规律以及科学原理进行智慧思辨，开展合乎逻辑的深度分析与逻辑推理，通过多元思考、举一反三形成有说服力的数学结论，掌握智慧解决问题的策略和思维方式。

3. 深度发展批判思维，形成科学理性精神、关键能力

《义务教育数学课程标准（2022年版）》指出：发展学生质疑问难的批判性思维，形成实事求是的科学精神，初步养成讲道理、有条理的思维品质，逐步形成理性精神［１］，这是对培养学生数学核心素养的客观描述。拥有数学高阶思维能够让学生的思维更加科学理性、严谨敏锐，更加善于质疑批判、反省思辨，更加聚焦问题疑难点、矛盾突出点、知识模糊点、方法切入点，追寻和探求数学知识的前世、今生与将来，数学问题的源头、本质与价值，从而形成科学理性的数学精神。

三、新版课标视域下数学高阶思维的培养策略

培养学生的数学高阶思维对提升学生的数学核心素养有巨大的促进作用，因此，每位数学教师应立足课堂，聚焦学生高阶思维进行深度打磨，不断反思与建模，实现入“模”后的华丽出“模”，最终发展学生的数学高阶思维。

1. 深度打磨，让高阶思维延伸力更加犀利

学生在进行数学学习时，教师要引导学生循序渐进、不断打磨和探索，寻找知识理解的适切方法、解决问题的不同策略，这样才能让学生高阶思维的触角延伸力更加犀利。

（1）精准捕捉认知生长点，在步步追问中不断推敲

数学学习一环紧扣一环，认知、思维生生不息，学生只有找准数学认知生长点，不断激活思维，才能让思维向深处延伸、在高处进阶。数学认知生长点包知识学习、问题解决、规律探索、思维拓展等方面。在这些数学认知思维生长节点上，教师要循序渐进、步步追问、不断深入、递进引领学生进行思考。

①数学知识的概念内涵是什么？本质特征是什么？优点和用途是什么？它后续生长点、连接点在哪儿？

②在解决问题时，是从问题入手反向思维简单明了，还是从条件入手正向分析思考清晰快捷？

③除了已展示的思路外，还可以从什么方向入手，如何列式解答，这几种解法有哪些相同点及不同点？这些方法、策略对今后解决问题有怎样的启发？

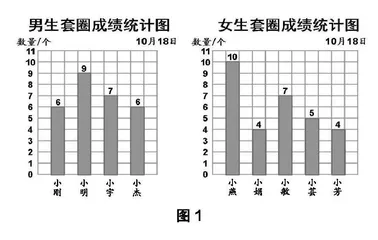
比如，教学“平均数”时，教师出示例题：四年级第一小组的男生、女生进行套圈比赛，每人套15个圈。如图1，统计图表示男生、女生套中的个数。男生套得准一些还是女生套得准一些？你想怎样比？你打算怎样求男生平均每人套中的个数？

当学生通过学习和探究，认识到“要先分别求出男生和女生平均每人套中的个数再比较，这种比较方法才合理”后，教师循序渐进、步步引领：如何操作才能直观、清晰看出“男生平均每人套中的个数”？学生经过自主思考、同桌讨论，积极交流想法：可以把小明9个中的1个移给小刚，1个移给小杰，每人的成绩都是7个。

教师追问：为什么要这样操作？你能给这种操作方法起个恰当的名字吗？学生纷纷答道：把小明多的个数移出来，补给少的，这样每个人套中的数量就是同样多；这种方法可以叫作“移多补少”。

在学生理解掌握“移多补少”方法后，教师启发：除了动手操作“移多补少”的方法外，还可以怎样得出“男生平均每人套中的个数”？学生纷纷回答：可以通过计算，先求出4个人套中的总个数，再平均分成4份。列式为：（6＋9＋7＋6）÷4=28÷4=7（个）。

教师追问：（6＋9＋7＋6）表示什么？28÷4表示什么？7表示什么？这种方法可以怎样简称？这样在学生充分理解算式的同时，清晰归纳出计算策略，即先合并（求总和），再平均分。

虽然学生已探索出“移多补少”及计算这两种方法，已经完成解答任务，但是教师应进一步启智引思：除了以上两种方法外，还有不同的方法吗？有部分学生经过个人深思及小组共同研讨，拓展出新的思路：在6的上面画一条线，求出6后面的平均数，再和6相加，即：（3+1）÷4=1（个），6+1=7（个），所以7是这组数的平均数（如图2）。

教师佯装不懂：这种方法和第二种方法有什么异同？学生的思维在深度反思中不断拓展进阶：虽然同样是计算，但是第二种方法是平均分总数，第三种方法是平均分6后面的部分，平均分的总数少。

探索到这里，教师可以进一步启发学生：女生平均套中的个数如何求？通过上面的思考与探索，对今后你的数学学习有怎样的启发？这样的思考使得学生的数学思维、数学学习形成整体性、结构化。

（2）精准把脉思维困惑点，引导学生在“愤悱处”反复琢磨

数学思维困惑点包括自我生成的思维困惑点和学生提出自己不理解的思维困惑处。当然，数学思维的困惑点不一定是低阶思维，是学生从低阶思维走向高阶思维的必经路线及突破口。针对学生自我生成的思维困惑点，教师要引导学生不能急躁与气馁，而应冷静思考、清晰审视：“我是没有真正理解概念还是不会动手操作实践？是不会举例验证欠缺逻辑推理，是思维过于机械还是钻进了牛角尖，方向跑偏了？”对于学生提出自己有同感的思维困惑处，教师也要引导学生进行深刻剖析、深度思考、反复琢磨，不断逼近问题的本质，只有如此学生才能打通思维堵点和思维断点。

比如教学“三角形三边关系”时，当学生通过操作、思考归纳出“三角形三边关系”即“三角形任意两边长度的和大于第三边”时，其实学生的理解大多只是明面上的理解，还比较肤浅，没有真正理解透彻。当学生面对教材练习题“先量出两根小棒的长度，再想一想，能和它们围成三角形的第三根小棒的长可能是多少厘米”时，学生反应不一：通过测量发现两根小棒分别长8厘米、3厘米，有的学生根据已经学的“三角形三边关系”，认为可以是8厘米，有个别学生不假思索地认为3厘米也是可能的，由此可见少数学生没有真正理解“三角形三边关系”，即怎样的三条线段能围成一个三角形。

为纾困解疑，打通学生思维困惑点，激活高阶思维培育路径，教师可以引导学生不断打磨，通过观察、思考3厘米是否是三条边中最短的，为什么？通过思辨推理，学生发现如果比3厘米还短肯定无法围成三角形。

教师再次追问打磨：8厘米这条小棒呢，一定是最长边吗？它存在几种情况？学生思考后发现8厘米可以是最长的，也可以不是最长的。如果8厘米是最长的，另外一条边最短是多少厘米？学生思考后得出应该最短6厘米，这样符合“三角形任意两边长度的和大于第三边”，同时可以引导学生，8-3=5，5<6，说明“三角形任意两边长度的差小于第三边”。如果8厘米不是最长边，那么可以用8＋3=11，说明最长边应该小于11，最长边最大为10厘米。综上可见，能和8厘米、3厘米它们围成三角形的第三根小棒长度小于11厘米、大于5厘米，即可能是10厘米、9厘米、8厘米、7厘米、6厘米。

2. 精心建模，让高阶思维拓优力更加灵活

数学学习过程中，学生如果能将数学思维恰当贯穿于学习的发生、发展与结果之中，多用“我是这样思考的……”“为什么这样做”“如果不这样还可以怎样”“除了这种策略外，我还想到”等具有思维深度的句式，就能真正关注思维的内在机理，让思维的火花不断绽放。

（1）精准剖析切入点，在比较中精益求精

数学学习过程中既要讲究思维方法的多样性，力求多点开花，又要从中寻找适合的、恰当的乃至最佳的思维方法。因为在学与教的过程中教师必须面对的是：是否需要对因思维发散而产生的各种方法进行必要的优化？答案不言而喻，数学中绝不是为了刻意追求“与众不同”的方法多样化与思维多样化。因为与单一追求“多元化解题方法”相比较，数学应力倡与践行思维的深化与优化，即应通过层层递进的关键问题将学生的思维引向深入，而不只是简单满足于“越多越好”。

比如教学“乘法运算律”时，当学生理解并探索出乘法交换律、乘法结合律及乘法分配律后，教师可以出示：44×25，让学生用简便方法计算，并思考能想出哪几种简便方法？学生经过独立思考后，分别得出以下几种方法：

方法一： 44×25

=（40+4）×25

=40×25+4×25

=1000+100

=1100；

方法二：44×25

=（4×11）×25

=4×25×11

=100×11

=1100；

方法三：44×25

=（2×22）×25

=2×25×22

=50×22

=1100；

方法四：44×25

=44×5×5

=220×5

=1100；

方法五：44×25