如何培养小学生的抽象思维能力

作者简介：郑春露（1998—），本科学历，中小学二级教师，从事小学数学教学工作。

郑春露  江苏省南通市新坝小学  226361

［摘  要］ 抽象思维是学生思维能力的重要一环，着眼于学生“抽象思维”培养的数学课堂教学，教师应从适当的角度切入，通过适切情境、探究活动、不断追问和多样练习等教学手段，发展学生抽象思维，促进学生抽象思维能力拔节生长。

［关键词］ 抽象思维；小学生；乘法分配律

数学学科由于其本身的抽象性和逻辑性，对于培养学生逻辑思维能力和提升学习能力的作用显著。事实上，数学教材多处呈现了抽象思想，在实际教学的过程中，教师要有意识地培养小学生的抽象思维。那么，教师应如何在教学中渗透抽象思想，从哪个角度切入培养学生的抽象思维能力呢？下面，笔者结合“乘法分配律”一课的教学，从四个方面来具体阐述培养学生抽象思维能力的有效策略。

一、适切情境：触发抽象思维动机

借助一切可行方式激发学生的求知欲望，引发学生的求学精神是每个教师需要长期思考的重要问题。众所周知，小学生思维呈现具体形象的特征，而数学学科知识抽象生涩，这就激发了二者之间的矛盾。如果教师能通过有效策略让矛盾得以化解，则可以从一定程度上触发学生的抽象思维动机。在教学中，教师要从学生的思维特征出发，创设适切的教学情境，把直观的学习活动与抽象的思维活动有机融合，促使学生在情境中感受数学的魅力，触发抽象思维动机。

片段1：创设情境，抛出问题

师：春天来了，到处绿意盎然。然而，前几年某些地方沙尘肆虐，春意被这漫天的沙尘所困扰，让祖国母亲日益衰老。谁能想出办法来改善当前的环境？（课件出示各处春天的图片，有优美风景，也有被沙尘笼罩的恶劣情景。学生观看后提出各种改善环境的方法）

师：刚才不少同学提出通过植树造林改善环境的好方法，那就让我们行动起来吧！

出示问题：三年级5班40名学生参加植树活动，全班每人种植1棵绒毛白蜡树（每棵树苗16元）和1棵桃树（每棵树苗14元），那么一共需要花费多少钱购买树苗？

从学生身边事物出发创设教学情境，可以有效引发认知冲突，快速激起学生对新课学习的兴趣。在课堂导入部分，教师创设了治理沙尘天气的教学情境，引发学生“植树造林”的需求，从而让后续问题的抛出顺理成章，使学生快速进入探索境界。在整个教学情境中，学生不仅经历了具体场景中提取数学信息的过程，充分感受到数学与生活的密切联系，还激发了抽象思维的动机。由此可见，适切的教学情境是触发抽象思维动机的有效方法。

二、探究活动：抽象思维的“脚手架”

关注思想方法的渗透、抽象思维的发展和数学素养的提高是探究活动的核心任务。数学探究活动为培养学生抽象思维提供了有效的“脚手架”，它能遵循学生抽象思维发展的规律，以学生的现有思维水平为起点，给予学生思维体验、享受、再体验的时间与空间，在这个过程中，学生的抽象思维水平得到深度提高。因此，教师要引导学生开展富有价值的探究活动，让学生通过主动探索积累充足的抽象经验，发展抽象思维能力。

片段2：展开探索，积累经验

师：购买树苗需要花费多少钱？请大家列式解答。（学生解题，教师巡视）

师：请说一说你们是如何解决这个问题的？

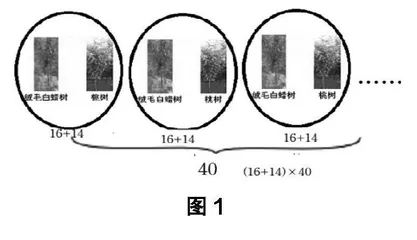
生1：我是将买1棵绒毛白蜡树与1棵桃树所需花费的钱数求出，再乘40，就得到总共的花费。（生1边画图边汇报，如图1）

生2：我是分别去求购买40棵绒毛白蜡树需要的钱数与40棵桃树所需要的钱数，再将两个数相加。（生2边画图边汇报，如图2）

师：生1和生2所列的算式不同，结果一样吗？

生（齐）：一样。

师：两人解题思路不同，谁能具体说一说他们的思路？

生3：生1是求的40个30是多少，生2求的是40个16和40个14一共是多少，所以两种方法的计算结果肯定一样。

师：非常好，事实上两种解法最终殊途同归。（教师课件出示图3）

探究活动是开展探究学习的有效方法，可以让学生在“做中学”，体验学习乐趣的同时培养抽象思维能力。本环节中，教师设计具体的探究活动，让学生在梳理具体情境的过程中理解数量关系，进行深入的思考和探索，最终自然地抽象得出等式“（16+14）×40=16×40+14×40”，并深层次领悟等式两边的意义，从根本上理解数学本质，同时获得抽象的思维经验。

三、不断追问：让抽象思维拔节生长

一般来说，随着年龄的增长，小学生的抽象思维水平会越来越高。因此，教师在教学中要从学生认知序列和思维发展特征出发，不断追问于学生的最近发展区，引导学生逐步剥离具体事物的外部特征，抽象得出事物的本质特征，从而在这样的思维活动中建立模型，发展抽象思维能力。

片段3：不断追问，建立模型

师：观察等式（16+14）×40=16×40+14×40，并试着再写出一组这样的等式。（学生观察后很快写出等式，教师巡视）

师：教师可以通过什么方法来验证这个等式是否正确？

生4：乘法的意义。

师：那这样的等式你们还能写吗？能写完吗？

生（齐）：不能。

师：事实上，这些等式中都藏着一个规律，即乘法分配律，这个规律具有普遍性。

师（拾级而上）：观察你们写出的等式，并试着将写不完的等式用你喜欢的方式进行表达。（教师课件呈现学生的作品后，学生又一次进入深度思考状态，很快有了结果，如图4）

教师要深钻教材，创新探究模式，相比“师讲生听”来说，学生抽象思维发展得更快。本环节中，教师以追问引导学生步步深入探索，亲历抽象规律形成的过程，从而抽象得出乘法分配律的语言表征、符号表征等，使得乘法分配律的字母模型呼之欲出。学生在对比、辨析和优化中，能深化对数学模型的理解，体验数学简洁美，促使抽象思维能力拔节生长。

四、多样练习：让抽象思维得能以深化

多样化的数学练习不仅能使学生达到巩固新知的目的，还能使学生的认知结构在不断调整中得以扩充，更重要的是能有效发展学生抽象思维。因此，在课堂中教师要从具体教学内容出发设计多样化的数学练习，引导学生在观察、分析、比较和辨析中抽象知识本质，让抽象思维得以深化。

片段4：分层练习，全面发展

基础性练习：据乘法分配律填写。

（7+125）×8=____________；a×7+7×5=___________。

提高性练习：判断以下等式是否正确，并说一说理由。

（1）（8+7）×125=8×125+7；

（2）（8+7）×125=8×125+7×125。

拓展性练习：

植物园中有一块长方形的菜园（如图5），原来的长为80米，宽为20米，现需扩大种植规模，长增加了30米，试求出现在这块菜园的面积。

富有挑战性的问题可以多维度激发学生的深度思考和深度探索。本环节中，教师没有限制学生的思维，而是让学生自主开展富有价值的对话和辩论，从对具体问题的探讨，到规律的归纳，再到模型的抽象，真正体现了层层递进的数学抽象过程。在这个过程中，学生对乘法分配律有了清晰和深刻的认识，充分感悟知识间千丝万缕的联系，真正深化了抽象思维能力。

总之，抽象思维是数学素养的重要范畴，是将学生的数学学习引向深入的载体。教师要通过创设情境、设计活动、不断追问和设计练习等教学方式，让学生的抽象思维能力以鲜活的方式拔节生长。