巧用微视频 发挥大作用

［摘  要］ 微视频具有短小、直观、形象等特点，将其应用于数学课堂教学中可以提升课堂活力，有效吸引学生的注意力，提高教学效率。借助微视频进行教学可以节约时间成本，给学生提供更多的时间去思考、探索、感悟，进而有效提升学生的学习品质和培养其数学核心素养。

［关键词］ 微视频；教学效率；学习品质

“鸽巢问题”是一个重要的数学模型，也是一种逻辑推理的方法。从学生实际学习反馈来看，学生能够熟记这个模型，也能直接应用这个模型解决一些特定结构的数学或生活问题，但是部分学生并没有真正地理解蕴含其中的数学原理，因此遇到一些比较灵活的问题时常常束手无策。为了改变这一局面，笔者将微视频引入课堂，借助微视频帮助学生理解“鸽巢问题”的数学本质，提高学生逻辑分析和逻辑推理能力，助力学生全面发展。下面，笔者以“鸽巢问题”的教学片段为例，展示微视频激活学生数学思维、丰富学生活动经验、激发学生学习兴趣等辅助教学功能，从而提高教学效益。

一、教学过程

1. 巧用微视频，感知模型

师：抢凳子的游戏大家玩过吗？

生（齐声答）：玩过。

师：谁来说一说游戏规则是怎样的？

生1：首先，将凳子摆成一圈，凳子数要比参加游戏的人数少1把；然后，参加游戏的几个人围着凳子转圈，当听到“坐”的口令时，参加游戏的人要抢坐凳子。因为凳子数比参加游戏的人数少1把，所以会有1个人抢不到凳子，抢不到凳子的人会被淘汰。每淘汰1人后撤下1把凳子，然后继续游戏，如此反复，直至得出冠军，比赛结束。

师：说得很好，表述清晰。今天我们要进行一个不一样的抢凳子的游戏。（教师课件出示游戏规则）

游戏规则：3个人围着2把凳子转，当听到“坐”的口令后，3个人必须全部坐在凳子上。

新游戏与学生心中的游戏有所不同，学生不知所措。

师：根据新游戏规则，会出现怎样的结果呢？

生2：1把凳子上要坐2个人。

生3：也有可能3个人挤在1把凳子上。

师：很好，我们现在看看视频中的小朋友是如何玩这个游戏的。

教师播放课前准备好的视频，让学生直观感知至少有1把凳子上要坐2个人。

思考：教师从学生已有的生活经验出发，选择趣味性的“抢凳子”游戏为切入点，通过更改游戏规则创设认知冲突，让学生快速进入学习状态。在教学中，教师先提供时间让学生猜想游戏中可能出现的结果，然后用微视频的方式播放游戏的实施过程及结果。这样既能验证学生的猜想，又能节省时间成本，同时还能提高学生的参与度，调动学生学习的积极性。通过微视频可以让学生直观感知“总有1把凳子上至少坐2个人”，并验证自己的猜想。生活中有许多“鸽巢问题”的原型，教师要有意识地从学生已有的知识和经验出发，选择贴近学生的生活情境加以展示，激发学生学习兴趣，为后续学习积累活动经验。

2. 巧用微视频，聚焦模型

师：将4支笔放进3个笔盒中，总有1个笔盒中至少有2支笔，你们认可这一说法吗？

（学生疑惑）

师：如果要解释这个问题，试想可能有几种不同的放法呢？大家以小组为单位，准备3个笔盒和4支笔，看一看共有几种放法？请大家用方框表示盒子，用“｜”表示笔，画一画几种不同的放法，能否得到以上结论？

教师放手让学生以小组为单位动手操作，并巡视指导，然后组织学生互动交流。

生4：可以将4支笔全部放在第1个笔盒里。

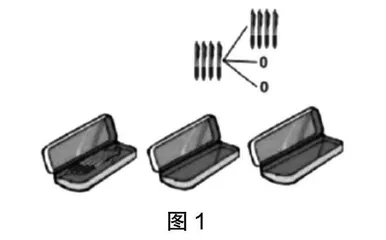
师：是这样吗？教师播放4支笔放到1个笔盒的视频。（学生点头表示赞成，教师出示摆放结果，如图1所示）

师：我们用（4，0，0）来记录这种放法。将4支笔同时放进1个笔盒里还有其他放法吗？一定要放在第1个笔盒里吗？

生5：可以将4支笔分别都放在第2个或第3个笔盒里。

师：很棒，如果用如上放法进行记录，你会吗？

生（齐声答）：（0，4，0）或（0，0，4）。

师：按照这种放法，不管怎么放，其中1个笔盒里都放了4支笔。在这里，如果不需要考虑具体放到哪个笔盒里，只考虑笔盒中笔的数量，可以将以上3种放法看成1种放法。

师：还有其他放法吗？

生6：在第1个笔盒里放3支笔，将另外1支笔放在第2个笔盒里，就是（3，1，0）。

教师根据生6的放法播放微视频，摆放结果如图2所示。

师：这里我们不考虑笔盒顺序，总有1个笔盒放进了几支笔？

生（齐声答）：3支。

生7：还可以将2支笔放在1个笔盒里，另外2支笔放在另外1个笔盒里，记作（2，2，0）。

生8：还有另外1种放法，2支笔放在1个笔盒里，剩余的2支笔分别放进另外2个笔盒内，记作（2，1，1）。

教师按照学生所说的播放微视频，最终得到如图3、图4所示的结果。

师：对于以上2种放法，总有1个笔盒放进了几支笔？

生（齐声答）：2支笔。

师：还有其他放法吗？

生（齐声答）：没有了。

师：综合分析以上4种放法，看看是否得到最初的结论呢？

学生积极思考，教师课件展示4种放法让学生对比观察。学生通过观察消除了之前的疑惑，认可了结论。

师：该结论中有哪几个关键词？你们如何理解呢？

在教师的启发和指导下，学生从结论中抽象出“不管怎么放”“总有”“至少”等关键词。对于关键词的理解是本节课研究的重点和难点，教师组织学生交流，了解学生的真实想法，以此加深学生的理解，突破难点。

师：谁来说一说，你们如何理解结论中的“总有”一词？

生9：肯定有，一定有。

师：“至少”如何理解呢？

生10：最少。

生11：我感觉用“不少于”来描述更恰当，也就是说一定有1个笔盒里的笔不少于2支。

师：说得真好，看来大家对以上结论已经理解得非常透彻了。

思考：教师将“抢凳子”游戏改编成“放笔”活动。活动之初，教师直接给出结论让学生理解，使学生陷入困境，此时教师让学生以小组为单位动手做、动口说，并利用微视频进行展示，通过多感官参与让学生观察、理解“鸽巢问题”的基本原理。在活动中，通过操作、观察等数学活动，为学生积累了丰富的感性素材，为理性思维的升华奠定了基础。教学中教师用微视频展示活动实施过程和实施结果，以此加深学生对“总有”“至少”的数学含义的理解，为后续建立“鸽巢问题”的模型积累了丰富的思维素材。

3. 巧用微视频，建立模型

师：我们刚才摆了4次得到结论，如果只摆1次，能否得到同样的结论呢？

学生积极思考，并通过动手画寻找解决问题的突破口，很快有了发现。

生12：我是这样想的，每1个笔盒里放1支笔，这样3个笔盒里共放了3支笔，剩下的1支笔放在任意1个笔盒里，这样不管怎么放，总有1个笔盒至少放进2支笔。

教师用微视频展示学生的操作过程。

师：结合视频的操作过程，请大家想一想，这种摆放其实是怎么分配的？

生13：平均分。

师：你能具体说一说，为什么要这样分配吗？

生13：这样可以最快地解决分几个的问题。

师：对于以上过程，用算式如何表示呢？

生13：4÷3=1（支）……1（支），1+1=2（支）。

师：现在我们用一些实例验证一下，看看大家能否依据该方法快速得到答案。

教师提出问题：

（1）如果7只鸽子飞进6个鸽巢，会是怎样的结果？

（2）如果100只鸽子飞进99个鸽巢，会是怎样的结果？

思考：通过应用枚举法，学生理解了“不管怎么放”“总有”“至少”等关键词。在此基础上，教师引导学生用“假设法”进一步猜想、验证，有效打通“鸽巢问题”模型的思维通道。在此过程中，学生提出自己的想法后，教师用微视频呈现假设思路，让学生直观感知平均分后剩1支笔必然产生的结果。通过微视频不仅可以给学生创造更多思考的时间，而且通过直观演示能够完整展示假设法的验证过程，加深学生对假设法的理解，提高学生的逻辑推理能力。假设法的本质是一种逻辑推理，教师通过微视频可以将这一抽象的逻辑推理过程直观地呈现出来，从而让逻辑推理有迹可循，有助于消除学生的畏难情绪，增强学生学习信心。在此过程中，教师通过平均分将思维过程和数学符号建立联系，帮助学生发现“鸽巢问题”的规律，从而为数学模型的建立埋下伏笔。

4. 巧用微视频，完善模型

师：不管怎么放，总有1个里面至少放2个。是不是所有类似的问题都是这一结论呢？如果将7支笔放进3个笔盒里，会得到怎样的结果呢？

生14：假设每1个笔盒中放2支笔，则3个笔盒放6支笔，剩下的1支笔任意放在1个笔盒里。不管怎么放，总有1个笔盒里至少放了3支笔。

师：很好，你能用算式来表示这一想法吗？

生14：7÷3=2（支）……1（支），2+1=3（支）。

师：很好，结合以上算式请大家想一想，这个至少数与什么有关呢？

生15：与商和余数有关，至少数＝商＋余数。

师：不错的想法，到底是不是这样的呢？现在我们一起思考这样一个问题：把8支笔放进3个笔盒里，会有怎样的结果呢？

问题给出后，很多学生不假思索地根据生15给出的模型得到这样的结果：不管怎么放，总有1个笔盒至少放进4支笔。学生给出的解释是8÷3=2（支）……2（支），2+2=4（支）。

师：很多学生给出的答案是至少放进了4支笔，你们认可这个说法吗？

教师给出问题后，学生进一步思考、验证。

生16：我不赞成这种说法，将8支笔放进3个笔盒里，每1个笔盒先放进2支笔，这样还剩下2支笔，而这2支笔不一定放在1个笔盒里，所以至少数应该是3。

师：分析得很有道理，请大家结合视频看一下，是不是这样呢？

教师播放8支笔放进3个笔盒里的视频。视频中先是展示平均分的过程，然后展示将剩余的2支笔放进同1个笔盒里和放进不同笔盒里的过程。

师：结合以上视频说一说，至少数和商到底存在怎样的关系呢？

教师预留时间让学生思考、讨论，最终学生达成共识：至少数＝商＋1。学生通过观察、思考、交流、推理、归纳等活动得到“鸽巢原理”。

思考：对于“鸽巢问题”，如果教师直接将“鸽巢原理”告知学生，学生可以直接通过套用来解决问题。但是不经历独立思考和自主探究的过程，学生将很难理解其数学内涵。基于此，本环节教师巧妙地设计问题引导学生将实际问题模型化，探索“至少数”与“商”的关系。在活动中，受定式思维的影响，学生很容易得到“至少数＝商＋余数”这一错误模型。为了突破定式思维的影响，教师适时地提出针对性问题进行交流，并结合微视频进行验证，以此顺利地建立《鸽巢问题》的数学模型。本环节借助微视频直观演示数学模型的建构过程，即尽量多地“平均分”笔，然后分配剩余的笔，剩余的笔无论分配到哪个盒子里，总有1个盒子的笔比平均分得到的笔至少多1个。借助视频的直观、形象帮助学生认清了“鸽巢问题”的本质，形成了“鸽巢问题”数学模型。

二、教学思考

在传统小学数学教学中，部分教师认为小学生的知识储备有限，自主学习能力相对薄弱，因此习惯“大包大揽”。在教学中，教师通过“灌输”的方式讲授知识，学生则“机械式”地背诵知识，这样的“教”与“学”不仅影响学生参与课堂的积极性，还会降低学生的数学理解能力，阻碍学生可持续学习能力的提升。笔者认为，教学中教师要创新教学模式，充分发挥多媒体技术的优势，全面展示抽象的数学知识，以此调动学生参与课堂的积极性，培养学生的逻辑推理能力。

在本课教学中，教师利用微视频直观呈现“鸽巢问题”，引导学生通过观察、猜想、操作、验证、分析等活动，主动参与“鸽巢问题”模型的建构，揭示了“鸽巢问题”的本质，促进学生发展思维能力和学习能力。

总之，在小学数学教学中，教师要不断更新教学观念，创新教学模式，充分发挥微视频的辅助教学功能，将抽象难懂的知识形象、直观地展示出来，让学生心情愉悦地投入到数学学习中，促进学生全面发展。