聚焦图形一致性，整体建构概念

［摘  要］ 特级教师黄爱华在教学“三角形的高”一课时，围绕三角形的组成元素聚焦图形的一致性，让学生在三角形面积变化中建构三角形高的概念。

［关键词］ 认识图形；三角形的高；一致性

随着《义务教育数学课程标准（2022年版）》（以下简称新课标）的颁布，图形的一致性、单元整体教学、教学评一致性等关键词成为教学的关注点。比如在图形概念教学时，教师应如何在教学设计中体现图形的一致性？如何重构课时进行单元整体教学？如何实现让学生从一节课的学习迁移到一类课的学习？近日，笔者观摩了特级教师黄爱华执教的“三角形的高”一课，深受启发。

一、交流知识联系，感悟路径一致性

师：同学们，我们在幼儿园初步认识了三角形，在一年级又一次认识了它，在四年级又有新的学习任务，到中学时还要继续深入地认识它。显然，三角形是一个非常重要的图形。当看到“三角形”三个字时，你们想到研究三角形要分几个步骤，一般涉及哪些内容？

生1：我们要先了解三角形的定义和学习三角形的特性；然后研究三角形的分类和研究图形的大小，可以根据角的大小或边的长短对三角形进行分类；最后研究图形的性质，比如三角形的内角和是180°。

师：我们一般要研究三角形的定义、特性、分类、大小和性质等，以及学这个知识有什么用处。当然，我们也可以从这几个角度来研究其他图形。

赏析：此片段黄老师开门见山地抛出学习的内容是三角形，引导学生回忆三角形的学习历程，梳理三角形的学习路径，为学习其他图形提供了范例。

二、经历学习过程，感悟高与面积的变化

1. 初步感受顶点位置与三角形大小的关系

师：这节课我们来研究三角形的大小，每个同学都先想一个三角形，然后想一个比刚才那个要大一些的三角形，你们通常会做什么事情？

生2：我会把边画得长一些。

师：假如我要在黑板上画一个三角形，这个点叫作点A，此时第二个点的位置很重要。如果点B近一些，AB边就短一些；如果点B远一些，AB边就长一些。假设我把点B定在这里，一条边就画出来了。此时同学们有没有感觉这个三角形的大小和AB边的长度有关系？点C的位置是不是有些地方不能随便点？

生3：点C不能在AB这条线段上，也不能在AB的延长线上。

师：（出示不同的两个点C）这两个点C有什么不同？

生4：第二个点组成的三角形，AC边和BC边会被拉得更长一些，这个三角形也更大一些。

师：AB边没变，C点远一些，这个图形的面积就会变得大一些，这是因为点C到AB边的距离变了。此时同学们有没有感受到图形的大小除了与AB边的长度有关，还与点C到AB边的距离有关，大家同意吗？点C再高一点，图形面积就大一点了。

赏析：“三角形的高”一课是第二学段“图形与几何”领域的教学内容。图形的认识教学要帮助学生建立几何图形的直观概念，帮助学生初步形成几何直观。黄老师通过与学生的聊天，不断激发学生的好奇心。黄老师通过精心设计每一个问题引导学生进行数学思考，让他们初步感受图形的大小不仅与AB边的长度有关，还与点C的位置有关，这是因为点C的位置决定着点C到AB边的距离。

2.研究三角形大小与哪些因素有关

师：我要把点C到AB边的距离画出来，应该画一条怎样的线？

生5：要画一条从点C到AB边中间的线。

师：这样的线有很多条，都可以吗？

生6：我觉得点C到AB边的距离是从点C到它的对边画1条垂线。

师：垂线就是从点C向AB画一条相交成直角的线，垂线可以画很长的，你们要说明它们之间的距离。

生7：把点C向下延长到AB 边，那个点设为垂足，点C到垂足之间的距离。

师：他说要画点C到垂足之间的那一条垂直的线段叫两点之间的距离，也就是你们学过的高。点C到AB边的距离就是画一条垂直的线段、垂直线段、垂线段，你们喜欢哪个？

生8：我认为是垂线段，不仅表达了意思，还更简洁。

师：（教师示范）老师把这条垂线段画出来。AB边的长度确定了，点C到AB边的距离确定了，是不是这个三角形的大小就确定了？如果我把点C移到这儿，AB边保持不变，点C到AB边的距离变长了，这个三角形的面积就变大了。所以看这两条线段的长度，AB边是三角形的底，点C到AB边的距离是三角形的高，由此能判断这个三角形的大小。

赏析：在这个环节中，黄老师不断追问“点C到AB边的距离”是直线还是线段、可以怎么画、怎么命名等，帮助学生明确点C到AB边的距离是一条垂线段，既要保持垂直关系，又是一条线段。同时，黄老师通过改变点C的位置，让学生发现点C位置的变化会引起点C到AB的距离的变化，从而改变这个三角形的大小。

3. 感受某点的移动会改变三角形大小

师：老师这个课件非常有意思，你们只要把这个三角形画出来，面积就算出来了。AB边保持不变，点C在这个位置的三角形面积是33.90平方厘米；把C点往上拉一拉，点C在另一个位置的三角形面积是41.91平方厘米。

师：我们再来演示一下，你们要看三个关键点：第一个看点C的位置，第二个想象点C到AB边的距离，第三个看三角形的面积。是不是距离越来越远，三角形的面积就越来越大？反过来距离越来越短，三角形的面积就越来越小？

生（齐声答）：是。

师：点C到AB边的距离就是垂线段。我们在研究三角形时，三角形的三条边和三个角是自己的，一定要研究三角形里可以画出这样一条高，高真正的含义就是图形里画出来的一条垂线段。高的画法是从顶点到垂足的这条线段，高表示的是顶点到对边的距离。三角形一般有三条高。如果垂足是D，我们说CD是三角形ABC的一条高。

赏析：科技给教学带来了便利，能让学生看到动态的演示过程。黄老师利用“几何画板”软件动态地展示点C的位置，通过移动点C的位置呈现三角形面积的数据，让学生感受一条底边保持不变，点C的位置会引起高的变化，从而使三角形的面积发生大小变化。

4. 引导学生圈出板书中的重点

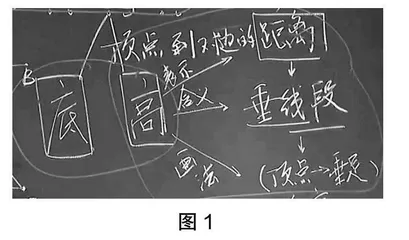
师：同学们，现在黑板上的板书（如图1）看不出重点，下面请小明同学用一支红色粉笔把重点的地方圈一圈，你们认为他会圈哪里？

生9：我认为他会圈“顶点到对边的距离”，因为顶点到对边的距离会影响图形的大小。

生10：我觉得他会圈“底和高”，因为底和高能直接影响整个三角形的大小。

生11：我感到他会圈“CD是三角形ABC的一条高”，因为这条高能影响三角形ABC的面积。

师：大家说得都非常棒！现在请同学们来圈，但在圈之前，先跟同桌讨论一个问题，这条高怎么是歪的？这条高是不是画错了？

生12：这条高是画对了的，因为AB边是斜着的。

师：定义→特性→分类→大小→性质是研究三角形的路径，这很重要，我把它圈起来。刚才我们聊了三角形的大小、距离、高、顶点及垂足，你们怎么看？

生13：我认为老师聊的是三角形的高是从顶点到底边的一条垂线段，而高的长度正好影响了三角形的面积大小。

师：你的第二句话真的太厉害了。老师特别想告诉你们高的作用，高的长度不一样，面积大小就不一样。

赏析：在这个教学环节中，黄老师使出了高明的一招：让学生用红笔圈重点。黄老师先组织学生进行同伴交流，再进行师生交流，提出“高变歪了”的质疑，最后让学生圈出板书的重点，凸显这节数学课的核心知识点之间的关联。

三、另辟研究方向，感悟三角形面积的不变性

师：刚才我们把点C上拉和下拉，还可以左拉和右拉。这个三角形ABC的面积是41平方厘米，现在我们决定把点C改成往左或往右拉，你们觉得会怎么变？

生14：我觉得如果点C往左右移的话，没有超过A和B，面积不变；如果超过A和B，面积就会变大。

生15：我觉得任意往左移或往右移，三角形的面积是不会变的，因为三角形的底和高都没有变。

师：（教师用软件演示）我们把点C往左拉，三角形的面积不变；把点C往右拉，三角形的面积仍然不变。同学们，老师在移动时始终让点C在同一条线上，这条线就是与AB边平行的线，两条平行线之间的距离是相等的，因此两条平行线之间的距离相等。虽然我们看到点C在左右移动，其实点C到AB边的高都还是这么长，所以三角形的面积不变。

师：同学们，我们再来看几组数据，点C往上拉、往下拉、往左拉、往右拉，拉来拉去是什么在变？

生16：高的长度在变。

师：高的变化引起了三角形大小的变化。

赏析：黄老师引导学生从点C的上下移动转向左右移动，借助“几何画板”软件动态地展示点C在同一条直线上的移动过程，不仅通过数据让学生直观地看到三角形面积始终保持不变，还让学生利用“两条平行线之间的距离相等”这个公理推断出三角形面积不变这个结论。这个学习过程能帮助学生感受学习高的价值，同时借助丰富的观察和想象活动能帮助学生建立高的概念。

综上所述，在教学“三角形的高”一课时，通常是单个数学知识点的教学，比如围绕高的概念、画高的方法等进行教学。黄老师教学“三角形的高”一课时采用由点到线：先让学生感受两个点的远近会导致边的长短发生变化；然后引出一个点，让学生感受这个点的位置会引起三角形高的变化，从而导致三角形的面积有大有小；最后让学生探寻当这个点在同一条直线上时，由于“平行线间的距离不变”验证了三角形的面积也不变。黄老师在三角形这个知识网络中帮助学生整体认识高这一元素，使学生不仅感受了高与三角形面积的关系，还感悟了图形学习的路径，掌握了更多的图形知识。