深化基础引导教考衔接 聚焦素养关注探究能力

［摘 要］2024年高考数学新课标Ⅰ卷持续深化高考改革内容，进一步加强对核心概念、重要原理、基本方法的深入考查，增加新颖性探究问题，聚焦考生数学学科核心素养，关注其思维能力与创新能力，发挥引导中学教师教学方向和服务拔尖创新人才选拔的功能。文章主要对2024年高考数学新课标Ⅰ卷的试题进行评析，并做出相应的教学建议。

［关键词］高考数学；教考衔接；试题评析；探究能力

［中图分类号］    G633.6                ［文献标识码］    A                ［文章编号］    1674-6058（2024）30-0021-04

2024年教育部教育考试院命制了4套高考数学试卷，分别是新课标Ⅰ卷（以下简称“新Ⅰ卷”）、新课标Ⅱ卷（以下简称“新Ⅱ卷”）、全国甲卷（文、理），两套新课标卷首次使用了19题模式，全国甲卷继续保持22题模式。其中，广东、浙江等11个省份选用了新Ⅰ卷，在历经5年的不断实践优化后，新Ⅰ卷成为新高考改革的方向指南。下面笔者对2024年高考数学新Ⅰ卷试题进行评价，并提出相应的教学建议。

一、试题评析

（一）深化基础性考查，引导中学教学

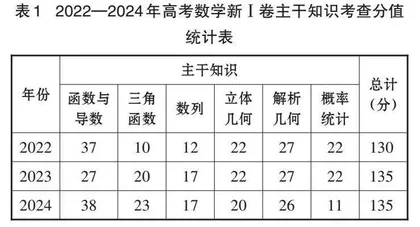
2019年教育部考试中心研制完成了《中国高考评价体系》［1］，确立了以“一核”“四层”“四翼”为理论基础的高考命题框架。其中“四翼”包括基础性、综合性、应用性和创新性，是高考的考查要求，基础性是“四翼”之首，是高考对素质教育的评价重要维度［2］。高考命题要进一步深化基础性考查，丰富其内涵，拓展考查途径，凸显基本概念、基本规律和基本原理的重要地位与作用，引导教学回归课标与教材，助力中学课程标准全面落实。这一命题要求在2024年高考数学新Ⅰ卷中得到了较好的体现。新Ⅰ卷试题围绕主干知识命制，加强对基本概念、基本原理的考查，旨在引导学生系统学习，避免死记硬背。通过对2022—2024高考数学年新Ⅰ卷主干知识考查分值的统计分析（见表1），笔者发现近两年主干知识考查分值达135分，占总分值的90％，其中函数与导数、解析几何、立体几何三大主干知识占比接近60％。这表明加强主干知识的考查是落实基础性考查的重要途径。

［例1］（2024年高考数学新Ⅰ卷第4题）已知[cosα+β=m]，[tanαtanβ=2]，则[cosα-β=]（ ）。

A. [-3m]        B. [-m3]         C. [m3]         D. [3m]

评析：试题以考生熟悉的教材习题为背景，以两角和与差的余弦公式为载体，考查考生对两角和与差的余弦公式的熟练运用及其内部联系的理解掌握程度。考生既可以根据两角和与差的余弦公式之间的关系解答，又可以直接运用和差化积公式解答，方法灵活多样。试题源于人教版（A版）高中数学必修第一册第255页复习参考题第15题第（1）小问：已知[cosα+β=15]，[cosα-β=35]，求[tanαtanβ]的值［3］。苏教版高中数学必修第二册第55页的例6直接给出了解答此类问题的一般方法和进一步学习与思考的问题。具体例题如下：已知[sinα+β=23]，[sinα-β=-15]，求[tanαtanβ]的值。例题提示学生据此推出用[α+β]，[α-β]的正弦与余弦表示[sinαcosβ]，[cosαsinβ]，[sinαsinβ]，[cosαcosβ]的式子［4］。试题以教材例题为背景命制，引导学生重视基本概念、重要公式、核心原理等基础知识的学习以及对教材例题与习题价值的挖掘，重视对学生数学学科核心素养的培育，为其后续发展打下坚实的基础。

（二）加强综合运用，考查关键能力

中国高考评价体系“四翼”中的“综合性”在数学学科中体现为知识间的内部联系，强调知识体系中各分支内容的相互交叉与渗透［5］。分析2024年高考数学新Ⅰ卷的内容笔者发现，第5题综合考查了圆柱与圆锥的侧面积、体积的计算，第11题在解析几何背景下考查了不等式问题的探究，第18题在导数问题中考查了曲线的对称性这一几何性质，第19题综合考查了新定义的数列与概率，考查学生对数学知识内在联系的掌握和思维的灵活性。

（1）若[b=0]，且[fx≥0]，求[a]的最小值；

（2）证明：曲线[y=fx]为中心对称图形；

（3）若[fx>-2]当且仅当[1<x<2]，求[b]的取值范围。

评析：试题第（2）问打破导数问题的命题套路，结合曲线[y=fx]的几何特征要求考生证明曲线[y=fx]为中心对称图形，命题立意较高，解法多样。考生既可以根据所学知识和方法来解答，又可以通过观察解析式的特点先猜想后证明，还可以运用高等数学知识解答。

思路1：由中心对称的几何特征入手，若曲线具有对称中心，则对称中心的横坐标必为定义域的中点，由于函数[fx]的定义域为[（0，2）]，故只需计算[f2-x+f（x）]为定值。由于[x∈（0，2），] [f2-x+f（x）=] [ln2-xx+a2-x+b1-x3+lnx2-x+ax+bx-13=2a]，故曲线[y=fx]是中心对称图形，对称中心为[1，a]。

思路2：从中心对称曲线的本质属性入手，函数[y=fx]的图象关于点[Pa，b]成中心对称图形的充要条件是函数[y=fx+a-b]为奇函数，也就是说，任何一个中心对称曲线都可以由奇函数的图象平移得到。通过观察函数[fx]的解析式发现，[y=x-13]是由[y=x3]向右平移一个单位得到，于是可以联想到探究函数[fx+1]的对称性，[fx+1=ln1+x1-x+ax+bx3+a]，由于[y=ln1+x1-x+ax+bx3]为奇函数，所以曲线[fx+1]关于[0，a]中心对称，从而曲线[fx]关于[1，a]中心对称。

试题通过对“中心对称”这一结构原理的深入考查，引导学生学习时注重对概念、原理等学科理论的本质属性进行深刻理解和熟练掌握，注重知识间的内在联系以及形成完整的知识结构和方法体系；引导教师在教学时注重培养学生面对学习探索问题时，能够高质量地分析和解决问题的能力。

（三）关注应用探究，聚焦学科素养

“应用性”是中国高考评价体系“四翼”的重要考查方面。为发挥高考的正向引导作用，命题坚持理论联系实际的原则，选用贴近生活、时代、社会的素材，以考查考生运用知识、能力及素养解决实际问题的能力。如2024年高考数学新Ⅰ卷中的第11题、第14题，就是考查考生知识迁移、学以致用的能力以及数学探究能力，聚焦考生的数学学科素养。

［例3］（2024年高考数学新Ⅰ卷第11题）造型<C：＼Users＼Administrator＼Desktop＼中学教学参考·文综版202410＼X10-8.tif>可以做成美丽的丝带，将其看作图1中曲线[C]的一部分。已知C过坐标原点O，且[C]上的点满足横坐标大于[-2]，到点[F（2，0）]的距离与到定直线[x=a（a<0）]的距离之积为4，则（      ）。

A. [a=-2]

B. 点[（22，0）]在[C]上

C. [C]在第一象限的点的纵坐标的最大值为[1]

D. 当点[（x0，y0）]在[C]上时，[y0≤4x0+2]

评析：试题素材类比圆锥曲线第二定义呈现，以研究圆锥曲线的一般方法为基础进行创新设计，考查考生在陌生情境下运用所学知识分析和解决问题的能力。下面逐一分析选项：A选项考查点与曲线的位置关系。设曲线上的动点[Px，y]，则[x>-2]且[x-22+y2×x-a=4]，曲线过坐标原点，故[0-22+02×0-a=4]，解得[a=-2]；对于B选项，曲线[C：x-22+y2x+22=16x>-2]，点[22，0]满足该方程；C选项可得出曲线的方程[y2=16x+22-x-22]，采用赋值法，取[x=32]，则[y2=6449-14]，此时[y2>1]，故曲线[C]在第一象限内点的纵坐标的最大值大于1；D选项考查曲线的方程特性，当点[x0，y0]在曲线上时，[y20=16x0+22-x0-22≤16x0+22]，满足[-4x0+2≤y0≤4x0+2]。综上，本题答案为ABD。

［例4］（2024年高考数学新Ⅰ卷第14题）甲、乙两人各有四张卡片，每张卡片上标有一个数字，甲的卡片上分别标有数字[1]，[3]，[5]，[7]，乙的卡片上分别标有数字[2]，[4]，[6]，[8].两人进行四轮比赛，在每轮比赛中，两人各自从自己持有的卡片中随机选一张，并比较所选卡片上数字的大小，数字大的人得[1]分，数字小的人得[0]分，然后各自弃置此轮所选的卡片（弃置的卡片在此后的轮次中不能使用），则四轮比赛后，甲的总得分不小于[2]的概率为                 。

评析：试题以计数原理为背景，以探索创新情境为载体，考查“四翼”中的应用性。考生在解答本题时可以采用“枚举法”，以类似“田忌赛马”的方式对数字进行排列后得出结果，此种方法须考虑甲的总得分为1，2，3分，对思维严谨性要求较高；也可以结合概率问题的解题经验，考虑解答排列组合问题中常用的“正难则反”思路，将问题转化为求甲的总得分小于2的概率。当甲得0分时，甲的选法为1，3，5，7，乙的选法为2，4，6，8，就1种情况；当甲得1分时，我们考虑甲哪一局得分，这时我们将乙的选法固定为2，4，6，8，则可能是甲第1局的得分，共7种情况；甲第2局得分，共3种情况；甲第3局得分，共1种情况。则甲的总得分小于2的概率为[12]，从而甲的总得分不小于2的概率为[12]。

2024年高考数学新Ⅰ卷和新Ⅱ卷都增加了数学探究问题，旨在加强对学生数学学科核心素养的考查。笔者所在研究团队以《普通高中数学课程标准（2017年版2020年修订）》中核心素养水平的划分为依据，对2024年高考数学新Ⅰ卷考查的核心素养水平进行了划分，结合胡凤娟、保继光、任子朝、陈昂研究的高中数学核心素养测评案例［6］，按照华东师范大学教育博士后科研工作站朱立明提出的高中生数学学科核心素养测评框架构建［7］，对2022—2024年高考数学新Ⅰ卷考查的核心素养水平进行划分，赋分计算，得到图2所示的统计结果。

从图2可以看出，新Ⅰ卷近三年对六大核心素养考查的占比基本趋于稳定，重点考查逻辑推理、数学运算、直观想象等核心素养。进一步分析发现，新Ⅰ卷近三年逐年加大对逻辑推理素养的考查，对数学运算素养的考查要求略有降低。这充分说明新高考试题在命制时更注重考生的数学探究能力，加大对试题思维量的考查，减少了繁难的数学运算，旨在凸显数学思维在拔尖创新人才选拔中的重要价值和功能。

（四）凸显创新思维，发挥导向作用

《教育部关于做好2024年普通高校招生工作的通知》指出，高考要注重考查学生的必备知识、关键能力和学科素养，引导培养探索性、创新性思维品质［8］。这一指导意见在2024年高考数学新Ⅰ卷中得到了很好的体现。

［例5］（2024年高考数学新Ⅰ卷第19题）设[m]为正整数，数列[a1，a2，…，a4m+2]是公差不为[0]的等差数列，若从中删去两项[ai]和[aj（i<j）]后剩余的[4m]项可被平均分为[m]组，且每组的[4]个数都能构成等差数列，则称数列[a1，a2，…，a4m+2]是[（i，j）-]可分数列。

（1）写出所有的[（i，j）]，[1≤i<j≤6]，使得数列[a1，a2，…，a6]是[（i，j）-]可分数列；