素养本位的初中数学大单元教学设计框架和模式研究

［ 摘 要 ］数学教育的目的在于促进学生的全面发展，即培育品格健全的人．素养本位的大单元教学，可促使学生将习得的数学知识与方法转化为相对应的各项素养．文章以“平面直角坐标系”的教学为例，分别从知识框架、教学内容与素养目标三个方面展开分析，并从“情境导入，构建概念”“深入探索，明晰要点”“建立坐标系，解决问题”“回顾总结，梳理归纳”四个方面展开研究．

［ 关键词 ］素养；大单元；教学设计；教学模式

随着新课改的推进，大单元教学与素养本位的教育理念受到广大教育工作者的关注，尤其是在“双减”政策的落地之后，该如何将两者深度融合，以真正实现深度学习呢？探索发现，从整体视域把握教学内容，基于结构化的视角设计教学方案，可促进“五育融合”，推进教育的高质量发展．为此，笔者以“平面直角坐标系”为例，从如下几个方面展开教学分析、教学设计与教学思考．

教学分析

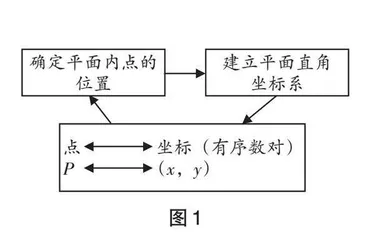
平面直角坐标系由数轴发展而来，展示了代数“数对”和几何“点”之间对应的关系．“数—式—方程—函数—图形”的发展，体现了人类思维由一维到二维的转变过程．平面直角坐标系作为重要的数学工具，对解决数学问题起到重要作用．（一） 知识框架分析平面直角坐标系章节知识点不多，但内在逻辑结构清晰，课前教师与学生一起将知识点梳理清楚，可帮助学生构建完善的单元知识体系．系统化的知识框架可让学生对所学内容产生清晰的认识．如图1，此为平面直角坐标系的单元知识框架图．

（二） 教学内容梳理

如表 1，针对单元知识点进行梳理，将主要内容罗列到表格中，可让学生对单元知识一目了然．

（三） 素养发展目标

素养本位的单元教学自然将培育核心素养作为首要目标，教学本章内容可发展学生的哪些核心素养呢？基于“三会”的视域来分析，可将平面直角坐标系章节所对应的素养目标做如下划分：

①会用数学的眼光观察现实世界，通过有序数对明确实际事物的位置关系，建立坐标系对事物位置进行描述，基于几何的维度发现并提出问题，发展学生的抽象能力、空间观念、几何直观与创新意识等素养；②会用数学的思维思考现实世界，引导学生在理论联系实际的基础上应用相应的数学知识解决问题，提炼数形结合思想，发展学生的推理能力、数学运算等素养；③会用数学的语言描述现实世界，借助坐标对现实生活中的位置加以描述，获得解决实际问题的能力，发展学生的数据观念、应用意识与模型观念等素养．

教学过程设计

（一） 情境导入，构建概念

情境：小明家门口有一条东西向的柏油路，从小明家出发，往东4米与7.5米处的路边分别有一棵柳树和一个小超市，往西4.8米与6米处的路边分别有一棵杨桃树和银杏树，请在草稿纸上画出该情境．与数轴确定点位置的方法进行类比，思考怎样明确平面内各个点所在的具体位置．

设计意图 从学生的生活实际出发，将学生所熟悉的生活场景作为情境素材，可拉近学生与课堂的距离．数轴与平面直角坐标系都涉及点的位置，该情境重点在于探寻点的位置，需要学生认真分析平面、直线、点之间的关系．学生在思考平面内各个点所在的具体位置时，主要是探索点在直线与平面上的“一一对应”的代数特征．

设计意图 数轴上关于原点对称的两个点具有“相反数”关系，是因为从平面内来观察，这两个点的纵横坐标互为相反数．借助图象展开探索，可让学生明确这一规律，此环节不仅渗透了数形结合思想，还有效发展了学生的推理能力．

4.动点的探索

探索5 已知数轴上的点 A 、 点B分别为 -3，5 ，若动点 M 以点 A 为起点，按照1单位/秒的速度朝数轴的正向缓慢移动，动点 N 以点 B 为起点，按照4单位/秒的速度朝数轴的负向快速移动，运动 t 秒后，点 M 、 点N 的位置分别为 -3 + t 与 5 - 4t ．

学生经自主探索与合作交流，提炼出的结论为：若 a 表示点 A ，那么点 A 正向运动 m 单位为 a + m ；负向运动 n 单位为 a - n ．

探索 6 若将平面直角坐标系内的点 A（5， - 2） 朝向左侧平移 3个单位，新的点坐标是什么？存在怎样的规律？若将点 A（5， - 2） 向下平移 5个单位，新的点坐标是什么？坐标变化规律是怎样的？

经探索与总结，获得结论为：在一个平面内，若点 （x，y） 朝向左侧或右侧平移 a 单位，那么新的点坐标仅需在横坐标的数值上加或减 a 个单位即可；若点 （x，y） 向上或下平移 b 个单位，那么新的点坐标仅需在纵坐标的数值上加或减 b 个单位即可．

设计意图 通过观察数轴上的动点与平面直角坐标系内的动点，发现它们的运动变化规律具有一致性特征．此为发展学生抽象能力、空间观念、几何直观与创新意识的过程．

（三）建立坐标系，解决问题

问题 1 某天下午一辆出租车一直在一条东西向的马路上工作，若将东向定位正向，西向定位负向，这辆出租车这半天的行驶记录分别为：+5，-3，+10，-8，-6，+11，-10 （单位：千米），那么这辆出租车送完最后一车客人时，与下午出发点之间的距离是多少？此时该车处于出发点的哪个位置？

问题2 已知四边形 ABCD 为长4、宽3的矩形，若将点 A 作为原点，以矩形中的 AB 边为坐标横轴建立平面直角坐标系，那么点 A，B，C，D的坐标分别是什么？

设计意图 对于将出租车的行驶路线展示在数轴上与借助矩形建立平面直角坐标系探寻点的位置这两个问题，都是通过回归数学本身，借助概念来解决的．如此设计，凸显了平面直角坐标系的工具性特征，同时促使学生学会用数学的思维思考现实问题，并从问题中提炼数形结合思想，发展推理能力、数学运算等素养．

（四） 回顾总结，梳理归纳

纵观以上整个探索过程，数形结合思想渗透在每个环节，贯穿整个教学流程．数轴是学生所熟悉的内容，以此为基础，借助类比思想探寻平面直角坐标系相关内容更加容易，这也充分体现了建构主义理论在教学中的应用．如表 3 所示，将数轴与平面直角坐标系的知识结构进行对照，可发现其中的异同点，为帮助学生从结构化的视角理解平面直角坐标系做好铺垫．

设计意图 以表格的模式进行课堂总结与归纳，不仅能帮助学生进一步梳理整个教学流程，厘清知识结构，还能帮助学生建立系统化的知识结构，凸显素养本位下的大单元教学的优势，为进一步发展学生的数学思维与提升学生的三会能力奠定基础．

思考与感悟

1.“大”处着手设计

大单元教学需立足于整体视域对教学内容进行分析与策划，因此在教学之前教师需基于“大”进行活动设计．如本节课，教师基于宏观的视角将知识框架、教学内容与素养发展目标等一一罗列清楚，为接下来的课时教学提供参考；同样，课堂伊始教师联系学生的生活实际设计教学情境，引导学生从中提炼关键性的概念，为学生深入探索夯实基础．这些都凸显了从“大”处着手设计教学的好处．

2.建构教学体系

没有一个知识是独立存在的个体，每个数学知识都有上下关联的内容．因此，教师在实际教学中应联系学生已有的认知结构与知识体系，进行教学内容的上下关联，让生活实际与数学知识进行深度融合，以降低学生理解的难度，从而帮助学生建构完整的知识体系．从教学流程来看，教师基于“大单元”的视角，将数轴与平面直角坐标系进行类比探索，帮助学生更好地实现新旧知识的融合，形成结构化的数学思维．

总之，素养本位的初中数学大单元教学中，教师需在明确单元主题的基础上，根据学情与教情设计恰当的课时活动，让每一个知识点都发挥承前启后的作用．学生在课堂教学中不断提升“三会”能力，发展“四基与四能”，真正达到发展核心素养的目的．