“生本”理念下的习题课探究

［ 摘 要 ］“生本”理念是一种具备人文关怀，促进学力发展的基本教学理念.文章以“圆与相似”的习题教学为例，具体从“旧知回顾，唤醒认知”“加强互动，探索相似”“逐层递进，深化理解”“实际应用，发展学力”四个方面展开研究，并从如下几点谈一些思考：根据课标要求授课，促进数学思维发展；精心挑选经典问题，逐步完善学生的认知体系；做好课堂引导工作，落实数学核心素养.

［ 关键词 ］“生本”理念；习题教学；圆与相似

“生本”理念强调尊重学生个性，挖掘潜能，让学生体验学习成就感，保持求知欲.这是一种人文关怀的教育理念，有助于学生长期发展.本文以“圆与相似”为例，探讨如何在习题教学中实践“生本”理念.

教学过程设计

1.旧知回顾，唤醒认知

建构主义理论认为，新知的构建是建立在学生已有的认知经验之上的.因此，在习题教学前，教师不仅要了解学生的实际认知水平，还要想方设法调动学生已有的认知经验，借助问题唤醒学生的认知，为更好地接纳新知做好铺垫.

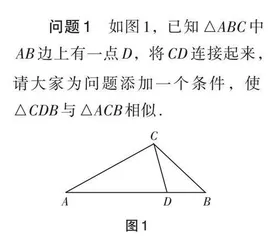
问题1 如图1，已知 △ABC 中AB边上有一点D，将CD连接起来，请大家为问题添加一个条件，使△CDB 与 △ACB 相似.

追问：如图2， △ABC 的外接圆为⊙ O ，延长 CD 与⊙ O 相交于点E，若要使 △CDB 与 △ACB 相似，应添加什么与圆相关的条件？

设计意图 提出两个开放性问题，旨在引导学生自主复习三角形相似的判定法则，激活学生的思维，提高他们的探索兴趣，为后续深入教学打下基础.教师视学生为课堂主人，通过观察学生设定的条件和解题过程，客观评估学生的认知水平，这对教学来说至关重要.

2.加强互动，探索相似

问题2 如图3，已知 AB 为⊙ O的直径， CD 为⊙ O 的弦， AB 与 CD垂直， P 为垂足 . 请证明： PC 2 =PA ⋅ PB .

学生独立完成证明后进行组内交流，教师巡视并记录下学生的对话.

生1：将 AC ， BC 连接起来，结合直径 AB 可知 ∠ACB 为直角，所以∠BAC = ∠BCP .所以 △APC △CPB 所以 PC 2 = PA ⋅ PB .

生2：将 AC ， BD 连接起来，先证明 △CAP △BDP ， 再 根 据 条 件PC = PD ，证明 PC 2 = PA ⋅ PB ；也可以将 AD ， BC 连接起来，应用相同的方法证明 PC 2 = PA ⋅ PB .

生3：通过弧 BC 与弧 BD 相等的条件，更容易证明 ∠CAB = ∠BCP .

生 4：将 OC 连接起来，则在Rt△PCO 中 ， PC 2 =OC 2 -OP 2 =PA⋅PB .

设计意图 这道题有多种解法，旨在鼓励学生独立思考并合作交流.这不仅能巩固他们的知识和解题方法，还能拓展他们的思维 . 通过合作，学生不仅可以学习同伴的优点，提高自我认知，还可以从不同角度理解圆和相似性的联系，为培养灵活思维和严密推理打下基础.

师：请大家自主调整问题2中关于“ AB 为直径， CD ⊥ AB ”的条件，并思考线段 AP，BP，CP，DP 之间具备怎样的数量关系.

在教师的提问引导下，学生先独立思考并画图分析，再以小组合作的方式探讨线段 AP，BP，CP，DP 之间的数量关系（如图4、图5）.

问题（1）相对简单，学生可自主完成证明过程 （略）. 对于问题（2），学生呈现出如下几种解题方法.

生 11： 连 接 BD 后 可 证 得△GFD △GCB ， △DGB △FGC ，由此得到 ∠BFC = ∠BDG = 45° .

生 12：由于 ∠BCD 与 ∠BFD 均为直角，故 B ， F ， C ， D 四点共圆（见 图 10）， 根 据 圆 的 性 质 可 得∠BFC = 45°

生13：过点 C 作 MC 垂直于 CF ，且与 BG 相交于点 M ，证得 △MCB△FCD 后发现 △CFM 为等腰直角三角形，因此 ∠BFC = 45°

设计意图 数学锻炼思维，多种解题方法能显著提升学生的数学思维能力.在新课标指导下，习题教学应贯彻以学生为中心的理念，鼓励学生主动思考，挖掘潜力，为创新意识打下基础.这样的教学设计有助于学生构建和完善知识结构，正确理解辅助线的作用，促进数形结合思想的渗透，从而提升学生的学习能力.

教学思考

1.根据课标要求授课，促进数学思维发展

义务教育数学教学注重培养学生的思维能力，教师通常设计合适的问题激发学生的认知冲突，引导他们积极思考和探索，为数学思维的发展打下基础.在本节课中，教师利用开放性问题激发学生的思维潜能，鼓励不同认知水平的学生根据自己的情况进行思考和探索，从而促进思维能力的发展.

课标为教学的方向标.在本节课中，教师基于课标要求，鼓励学生主动参与课堂学习，通过思维拓展来识别问题核心，并通过解决一个问题来掌握解决同类问题的技能.学生从简单问题开始，随着变式难度的提升，思维能力得到发展，并在合作中互补，构建起完整的认知结构和解题技巧.本节课通过设计问题3，采用一题多解的变式方法，引导学生自主观察和思考，多角度分析问题，融入了转化和数形结合等数学思想.

2.精心挑选经典问题，逐步完善学生的认知体系

何为“生本”？顾名思义就是以生为本.学生是课堂的主人，课堂教学旨在帮助学生构建知识体系，引导他们通过解决问题提升认知能力，为发展数学核心素养打下基础.在数学教学中，应基于“生本”理念设计习题.少量但精炼的问题能深化学生的探索，促进深度学习，从而增强学力.

在课堂教学中，教师应为学生的思维活动留下足够的时间与空间，充分展示学生的思维过程，引导学生用不同的方法、不同的思路进行探索证明 ［1］ .教师出题和提问是学习的关键 . 深入研究问题有助于提升学生的成绩和数学素养 . 本节课采用“由顶向下”的教学方法，提出三个核心问题及其子问题，提高了学生对问题的敏感性 .这有助于学生在遇到类似问题时迅速应用解题策略，实现知识和解法的融会贯通.

3.做好课堂引导工作，落实数学核心素养

学生虽是课堂的主体，但教师的引导同样重要.教师提出开放性问题时，若不加以适当引导，可能会使学生思维偏离教学目标 . 有效的“生本”教学应平衡学生的参与和教师的指导，确保学生的思维能力能正确发展 . 本节课强调以学生为中心，鼓励自主学习和合作学习，同时在关键时刻提供指导，以培养学生的数学核心素养.

总之，新课标下的数学教学应关注学生行为和教师引导，强调师生互动以促进教学效果 . 设计基于“生本”理念的习题教学是顺应时代趋势，实现核心素养的关键.

参考文献

［1］周建拥 . 习题课教学的源头活水：以南通市级公开课“圆与相似”习题课教学为例 ［J］.初中数学教与学，2024（8）：21 - 24.