聚焦复习教学 发展核心素养

［ 摘 要 ］复习课是初三数学教学的主要课型之一.上好复习课，不仅能促使学生系统化地掌握数学知识，还能有效发展学生的数学思维，为培育数学核心素养奠定基础.文章以“特殊平行四边形”为例，从“回顾旧知，唤醒认知经验”“合作学习，互动深化理解”“课堂总结，积累学习经验”三个方面设计复习教学，并从“复习教学离不开精心组织”“复习教学需注重经验积累”“复习教学以发展素养为目标”三个方面谈一些思考与感悟.

［ 关键词 ］复习教学；特殊平行四边形；核心素养

复习教学旨在引领学生以更广阔的视野，深入梳理与整合已学知识.通过精心构建的知识框架，揭示各知识点之间的内在联系，引导学生从结构化的角度系统掌握数学知识，进而实现知识、方法与能力的深度融合与提升.复习教学对落实新课标的要求，培育学生的核心素养具有重要的价值与意义.在“双减”背景下，该如何落实课标理念，充分发挥好复习教学的价值呢？本文以“特殊平行四边形”的一轮复习为例，从多个维度深入探索与研究其内涵与外延.

教学设计

1.回顾旧知，唤醒认知经验

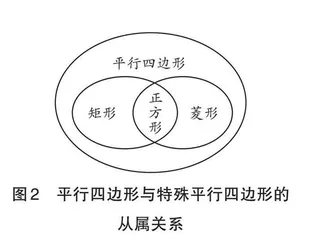
课堂伊始，教师展示图 1，带领学生一起回顾特殊平行四边形的相关知识，以唤醒学生的认知经验，为本节课的复习教学奠定基础.

在参照图 1 的基础上，引导学生探讨平行四边形、矩形、正方形与菱形之间的关系，并展示出来（如图2所示）.

师：大家是否还记得，我们是从什么角度去探讨四边形性质的呢？

生 1：从四边形的边、角、对角线与对称性等角度去探讨的.师：请大家分别谈一谈各个特殊四边形的性质.

生 2：可以将它们的性质罗列在一张表格中，以便更好地展示与比较.

师：这是个不错的想法，现在请大家在草稿纸上进行详细的整理与归纳.

教师从学生整理的结论中筛选出典范之作进行展示（见表1）.

师：大家还记得各种四边形的判定方法吗？

学生归纳总结，分别罗列出平行四边形、矩形、菱形、正方形的常规判定方法（略）.基于此，教师呈现一道中考真题供学生思考.

真题1 已知平行四边形 ABCD的对角线 AC 与 BD 在点 O 处相交.

（1） 若想让四边形 ABCD 成为菱形，可以添加________条件；

（2） 若想让四边形 ABCD 成为正方形，可以添加________条件，至少需要添加________个条件；

（3） 若想让四边形 ABCD 成为矩形，可以添加________条件.

设计意图 对四边形从属关系、性质及其判定条件的回顾，不仅帮助学生复习了旧知，激活并深化了认知经验，还增强了学生动手、动脑与整理的能力.中考真题1属于开放性问题，灵活度高，置于此处，旨在考查学生对特殊平行四边形基本概念的理解程度，对后续教学具有参考价值.

2.合作学习，互动深化理解例 1 如 图 3， 已 知 点 P 为△ABC 中 BC 边上的一个动点，经过点 P 作 DP 与 AB 平行，与 AC 边相交于点 D ；再作 EP 与 AC 边平行，与AB 边相交于点 E .

（1） 图中的 ADPE 是一个什么图形？

（2） 四边形 ADPE 有没有可能为正方形、矩形或菱形？

（3）动点 P 运动至什么位置时，ADPE 为菱形？理由是什么？

（4） 如果确定四边形 ADPE 是一个菱形，那么线段 AP 具备什么特征？

（5） 结合以上结论，尝试将一张三角形纸折叠两次，形成菱形，并说明折叠方法与获得菱形的具体理由.

（6） △ABC 需满足什么条件，可使四边形 ADPE 为矩形？

（7） 点 P 处于什么位置，且△ABC 满足什么条件，可使四边形ADPE 为正方形？

真题2 已知平行四边形 ABCD的两条对角线 AC，BD 互为垂直关系，且于点 O 处相交，添加一个条件，可确定四边形 ABCD 是正方形.

真题3 如图4，已知点 O 为矩形 ABCD 对角线 AC 上的中点，过点O 作 FE ⊥ AC ，分别与 BC ， AD 边相交于点 E ， F ，连接 AE，CF .

（1） 证明四边形 AFCE 为一个菱形；

（2） 如果 ∠FCD=30° ， AB= 3 ，那么四边形 AFCE 的面积是多少？设计意图 此环节运用一道例题引出一系列问题，引领学生循序渐进地深入探究，逐步揭示问题的本质.同时激活学生的思维，让学生在手脑并用的情况下，深化对特殊平行四边形动点问题的认识，并促进数学直观与逻辑推理能力的发展.

例2 如图5，已知点 O 为矩形ABCD 对角线 AC 的中点，一条过点O 的直线分别与 AB，CD 边相交于点E，F ，将 BF 连接起来与 AC 相交于点 M ，分别连接 BO，ED 后，明确∠BOC = 60° ，且 OF = CF .现有如下结论：① BF 为线段 OC的垂直平分线；② △OBE △MBC ；③ ED=EF ；④ S △AEO ∶S △BMC =2∶3 .以上结论正确的有________（填写序号）.

真 题 4 如 图 6， 已 知 矩 形ABCD 的 AB 边的长度为 8 ， BC 边的长度为 4，点 E 为 AB 边上的一点，点 F 为 CD 边上的一点，点 H ， G 位于对角线 AC 上 . 如果 EGFH 为一个菱形，那么 AE 的长度为（ ）

设计意图 此环节的例 2 将结论隐藏起来，需要学生基于问题条件展开思考与分析，由此激发学生的想象力.例2是一道极具挑战性的题目，对学生的思维能力提出了较高要求.将此题作为课堂复习的典范案例，可有效激发学生的探索欲，增强学生的学习信心.例题与真题的协同应用，能够显著拓宽学生的知识视野，并深化其数学理解能力，为学生的深入学习奠定坚实的基础.

3.课堂总结，积累学习经验

要求学生从不同维度总结本节课所复习的内容.具体而言，学生围绕知识点、思想方法、数学思维、能力和素养等方面展开总结：知识点方面，课堂探索的主题为特殊平行四边形，主要从知识网络、四边形的从属关系以及性质等展开分析；思想方法方面，本节课主要涉及的数学思想方法有转化与化归、分类讨论和数形结合；数学思维方面，涵盖了逆向思维、发散性思维等；能力和素养方面，培养了逻辑推理、直观想象等能力和素养.

设计意图 对于复习教学来说，课堂总结环节异常重要.层次清晰、重点突出的总结模式能帮助学生进一步厘清知识结构、思想方法，提升能力和素养，这些都是深度学习的表现，也是提升学力不可或缺的组成部分.实践表明，课堂总结并非单纯地梳理知识点那么简单，还需要从不同维度进行深入思考与分析.通过过程性评价和及时反思，系统地整理与分析所学内容，可以帮助学生培养良好的学习习惯，为核心素养的落实奠定坚实的基础.

教学思考与感悟

1.复习教学离不开精心组织

虽说学生是课堂的主体，课堂教学应当贯彻“以生为本”的理念，但教师作为课堂的组织者，其作用不容小觑.教师在课堂上的组织作用具有以下两方面的深远意义.

（1）组织教学内容

对于复习课来说，首先要明确复习的主题是什么，教师只有准确把握好数学的本质和学生的实际认知水平，才能设计出科学合理的教学方案.本节课探索的主题是特殊平行四边形，包括学生所熟悉的正方形、菱形与矩形.由于本节课为一轮复习课，因此需从最基础的图形的概念、性质、从属关系等维度出发，由浅入深地展开分析，以帮助学生积累学习经验，为灵活应用相应知识解决实际问题夯实基础.

（2）组织教学活动

恰当的教学方式可有效激发学生探索的兴趣，提升学生学习的积极性 . 本节课，教师结合学情与教情，精心组织了教学活动.通过积极的互动与交流，师生共同揭示了各类特殊四边形之间的内在联系，同时营造了一个积极向上的学习氛围，鼓励学生主动探索、深入思考.这一过程不仅发散了学生的思维，还帮助他们构建了完整且系统的知识体系，为日后形成结构化的认知奠定了坚实的基础.

2.复习教学需注重经验积累

学生在复习过程中不断积累知识，完善认知结构，并逐渐形成强大的应用能力，是复习教学的核心目标之一.那么，应当如何有效地激发学生的学习兴趣，让他们在复习过程中不断积累并丰富自己的经验呢？

在回顾旧知的环节中，教师鼓励学生梳理和总结知识结构，成功唤醒了学生的认知经验.如此设计，相较于传统的以定义、性质及判定方法为首要复习内容的教学模式，无疑展现了更为卓越的优越性.在合作学习的环节中，教师所展示的例题与中考真题都是经过精心筛选的.目的有二，一是让学生通过解决这些问题真正掌握知识的本质，二是让学生零距离感受中考的难度.

3.复习教学以发展素养为目标

新课标背景下的数学教学，不论什么课型都以发展学生的数学核心素养为目标.《义务教育数学课程标准 （2022年版）》明确提出：要让学生通过义务教育阶段的数学教学，获得适应社会生活必备的基础知识、技能、思想与经验 （简称“四基”），并形成发现、提出、分析与解决问题的能力 （简称“四能”）.“四基”与“四能”是发展核心素养不可或缺的一部分.

本节课，教师鼓励学生动手折叠菱形，这一过程深刻体现了“做中学”的教育理念，旨在通过实践操作加深学生对特殊平行四边形更为直观且深刻的理解.随着实践、猜想与验证活动的开展，不仅夯实了学生的“四基”，还有效发展了学生的“四能”.

总之，复习教学并非单纯的知识重复，而是一个深度加工的过程，它要求我们基于结构化的视角，系统地梳理、整合并提炼知识.复习教学对提升与巩固学生的思维能力具有重要价值与意义，也是落实核心素养的必经之路.