初中数学教学中跨学科融合的实践研究

［ 摘 要 ］分科教育在带来教学效果的同时，也存在着诸多不足，制约着学生素养的发展.跨学科教学最为显著的特征在于为学生构建了一个跨越学科界限的学习实践环境，它使学生在学习数学的过程中，能够自然地融入并应用其他学科的知识乃至方法，从而深化对数学知识的理解和应用能力.初中数学教学中跨学科融合的切入口应当在知识和方法两个方面.其实践途径是：基于教学内容的研究，在深刻理解初中生认知特性的前提下，判断教学内容中潜在的跨学科教学实践的切入口.随后，在具体的教学实践过程中，基于学生对数学知识和方法的理解，实现跨学科的融合，以及数学学科核心素养的有效发展.

［ 关键词 ］数学教学；跨学科融合；实践研究

目前，一线教师普遍习惯并视分科学习为理所当然的教育模式.然而，这其实是教育发展和改革进程中的一个阶段性产物.分科教育确实有助于学生对各学科知识实现精准且深入的掌握，从而提升教学效果.但与此同时，它也伴随着诸多不容忽视的局限性，这些局限性极大地阻碍了学生形成跨越学科界限的综合性视野，并限制了他们将所学知识有效应用于实践，进而对学生素养的发展构成了制约.《义务教育数学课程标准 （2022 年版）》（下文简称新课标） 明确提出数学教学要以发展学生的数学核心素养为目标，这意味着新课标背景下的初中数学教学需要开辟新的实践途径；新课标还明确提出设立跨学科主题学习活动，这是一种新的教学思路，是分科教学向综合性学习回归的尝试.已有研究表明，这种新颖的教学思路着重强化学科间的相互关联，倡导通过跨学科的教学实践，引领课程的综合化实施.目前，摆在一线教师面前的实际问题是：在构建基于学校课程和学生学情的跨学科课程体系的过程中，如何以数学学科为主体进行跨学科主题学习的设计与实施呢？有研究指出，这需要紧密关注学情与教情，通过实践深刻认识到主题是跨学科课程的核心组织要素.同时，协同不同学科教师，基于生活中的“真问题、真情境”，以及学生的认知基础、兴趣体验，设计多维度、适合学生个性化发展的主题 ［1］ .下面以人教版数学八年级下册“勾股定理”的教学为例，谈谈笔者的一些思考、尝试与反思.

初中数学教学中跨学科融合的切入口选择

所谓数学跨学科教学，通常被理解为是以数学为核心知识载体，融合其他学科知识，解决真实情境或 生 活 中 的 实 际 问 题 的 学 习 活动 ［2］ .相较于分科教学，跨学科教学的核心在于为学生打造跨学科的学习实践体验，使学生在数学学习中借鉴并运用其他学科的知识与方法，深入理解并掌握数学知识和方法，实现知识和方法的融会贯通与综合运用.根据以往教学改革的丰富经验，初中数学跨学科教学所追求的核心，应当是构建以数学学科为主体，促进多学科深度融合的教育模式 — —作为融合，它绝非简单的叠加或生硬的拼凑，而是将多学科知识于无形中融为一体，促使学生在数学学习过程中自然而然地将其思维延伸至其他学科，然后又将其他学科的知识或方法回馈于数学学习之中.因此，这里就浮现出了一个重要问题：在初中数学教学中，跨学科融合的切入口在哪里？

针对这个问题，笔者提出以下两点作为回应：

一是知识切入口.基于数学学科的跨学科教学，要以数学知识为基础.数学知识在形成的过程中，通常与其他学科有紧密的联系.在此情境下，教师应当具备敏锐的洞察力，适时评估知识跨界的契机，以判断其是否有助于加深学生对数学知识的理解，以及是否能更有效地引导学生将数学知识融入日常生活实践中.如果答案是“能”，那么跨学科教学实践的切入口就有了存在的价值.

二是方法切入口.数学思想方法独具特色，且具备迁移性，其基于数学逻辑与理性的运用方式，与其他学科中的某些思想方法存在共通之处，这为学科间的融合提供了契机 . 在此情境下，教师需要审慎判断，评估是否有必要从方法层面将数学思想方法迁移至其他学科，以便在学科交叉领域中找到新的切入口，更有效地促进知识的整合与应用.

“勾股定理”作为初中数学领域内的关键知识点，其揭示了直角三角形三边的数量关系，它不仅与我们的日常生活息息相关，还与直觉推理及逻辑推理相辅相成，是理解几何世界的重要依据.因此，在引导学生开展探究活动时，可以从知识与方法两个方面去评估.在教学设计时，教师不妨从学生的角度出发，预设其学习过程，进而在知识生成或方法应用的环节中，审视跨学科教学的价值所在.这样，便能有效拓展跨学科教学实践的广阔空间.可以说，对于初中生而言，认识到数学学科在众多学科中的独特价值及其在生活各领域的广泛应用，是至关重要的.这不仅能够有效培养学生对数学学科的认同感，还能深化他们对数学“基础性”地位的理解，进而激发学生内在的学习与探究动力.当然，这两个切入口并不是截然分离的，很多时候是相互融合的.因此，学科融合实质上是学科知识与方法的深度融合.

初中数学教学中跨学科融合实践途径例析

在具体的教学实践中，跨学科教学实践及其有效融合，对于教师而言，需要认识到其“意义”和“途径”.宏观层面的“意义”，在于其可以让学生在跨学科内容的探索与实践中获得对数学知识的独到理解、促进数学知识的迁移应用、推动数学知识的创新发展，促进学生数学核心素养的发展 ［3］ .实践层面的“途径”，需要这样概括：基于教学内容的研究，在深刻理解初中生认知特性的前提下，判断教学内容中潜在的跨学科教学实践的切入口.随后，在具体的教学实践中，基于学生对数学知识和方法的理解，实现跨学科的融合，以及数学学科核心素养的有效发展.

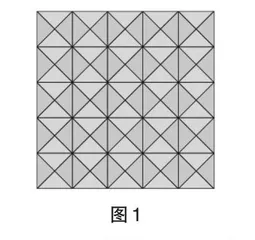
在介绍勾股定理时，人教版教材中有这样一段引入性描述：相传2500多年前，毕达哥拉斯有一次在朋友家做客时，发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系．我们也来观察一下地面的图案 （如图1），看看能从中发现什么数量关系.在证明勾股定理时，还有这样一段描述：以等腰直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的大正方形的面积．即等腰直角三角形的三边之间有一种特殊的关系：斜边的平方等于两直角边的平方和.

通过观察可以发现，人教版教材在跨学科教学方面的设计蕴含着丰富的启发性：其一，通过提供相关的历史史料来激发学生对勾股定理的探索兴趣，这一做法与历史学科紧密相连.在具体的教学设计中，还可以进一步拓展，比如引导学生关注“勾股树”等，以此来增强他们的学习兴趣与理解深度.其二，研究地砖图案，既与美术视角下的艺术形象紧密相连，又恰如其分地映射 了 数 学 研 究 的 精 髓 对 象 — —“形”.在具体的教学过程中，引导学生通过绘制“勾股树”的方式，可以进一步加深他们对勾股定理的理解与掌握.除此之外，当学生深化对勾股定理的理解时，可以将数学理论与日常生活相结合，运用数学与生物学的共同视角，去探索自然界中“智慧的植物” — —牵牛花的奥秘，研究它在生长过程中环绕树木攀升的“最短路径”，探寻其中蕴含的数学魅力……

根据前述分析，“勾股定理”的跨学科教学实践应聚焦于以下三个环节来展开 （下文仅阐述与跨学科相关的内容，其余与传统教学无显著差异，故不赘述）.

环节 1：引导学生在数学与历史融合的视角下，打开探究勾股定理的大门.

数学家、哲学家毕达哥拉斯在生活中的发现，对应着数学核心素养中的数学抽象，而这段探究史则是打开勾股定理探究大门的一把钥匙.在教学中，建议先展示图1，引导学生进行观察和探索.根据初中生的认知水平，他们此时可能无法想到去研究三角形三边之间的关系.当学生在初步探究中遭遇“愤悱”这一心理困境时，教师可适时地介绍毕达哥拉斯的发现，借此引发学生“思考”与“领悟”.

环节 2：引导学生在数学与美术融合的视角下，加深对勾股定理的理解.

这个过程主要是引导学生去画“勾股树”. 基于笔者的实践经验，在此阶段，可以先向学生展示勾股树图片，随后移除图片，引导学生亲手绘制勾股树.此时学生的注意力主要集中在两个关键点上，一是如何让画作显得更为美观，这与美术领域的追求息息相关；二是如何精确地绘画，这一需求与数学领域的严谨性相吻合.学生在此过程中边画边悟，能深刻体会到勾股定理的规律在不断重复展现，最终构成的“树”形图案，实则是数学图形演绎与生活中树木形象及大脑中树之表象的巧妙对应.这一过程赋予了“勾股树”独特的数学与艺术之美.学生的这种领悟，无疑是数学与美术完美融合的结晶.

环节 3：引导学生在数学与生物学融合的视角下，认识勾股定理的实用价值.

学生对“最短路径”问题并不陌生，但在现实生活中，生物成长与“最短路径”之间的联系却鲜为学生所了解.教师可以利用动画生动展现牵牛花在树木间蜿蜒盘旋的景致，随后逐步展开其蔓延的路径.学生会惊奇地发现，当将其完全展开后，它竟是一个完美的直角三角形.而牵牛花的蜿蜒路径，恰好与起点至终点的线段相呼应……通过数学与生物学的巧妙融合，学生对勾股定理的理解将达到更深的层次.

初中数学教学中跨学科融合的反思及总结

在“勾股定理”的教学案例中，数学与历史、美术及生物学的巧妙融合，贯穿于各个教学环节.在学生的学习体验中，这种跨学科学习的方式显得尤为流畅，毫无突兀之感，更无生硬拼接的印象.学生仿佛自然而然地穿梭于数学与其他学科之间，享受着知识交融的愉悦与启迪.教师巧妙构思的跨学科教学活动，为学生深入理解勾股定理带来了全新的体验，这一体验对于学生的数学学习以及对数学学科的深入认识有着显著的帮助.学生数学兴趣的增强是显而易见的，因为他们意识到，曾经认为枯燥无味的数学，实际上在各个学科中都有着不可或缺的价值.这种悄然形成的学科归属感，为学生学习数学提供了持久而稳定的动力.同时，学生在跨学科的学习过程中，确实能够对所学的数学知识有更深入的理解.如果仅从数学的视角来看，勾股定理可能只是一个简洁的数学公式；但若从跨学科融合的视角来观察，它不仅代表了数学领域的一段趣味历史，也体现了“勾股树”的美学价值 （同时包含学生在绘制“勾股树”过程中美学认知的构建），以及自然界生命的奇妙现象……所有这些元素，都展现了跨学科融合的深远意义.

总结过往实践经验，跨学科课堂的构建成功实现了数学与其他学科的深度融合，有效降低了学习难度，显著促进了学生跨学科思考能力的培养.展望未来初中数学教学的发展，在强化学生综合能力培养的大背景下，数学作为基础学科，必将与其他学科展开更为紧密的合作与融合，为学生开辟更广阔的学习空间，提升学习层次，这恰是数学学科核心素养培育所追求的目标与方向.

总而言之，初中数学教学应当积极倡导跨学科教学模式，致力于实现数学与其他学科的深度融合.跨学科融合教学方式，可以为学生创造更加丰富多彩的数学学习体验，进而丰富数学教学的内在价值，并拓展其外在边界，最终共同营造出一种更加优质的数学学习环境.

参考文献：

［1］刘超 . 以初中数学学科为主体的跨学科主题学习的设计与实施 ［J］.中国教育学刊，2024（4）：107.

［2］周青松，李明树，王晓峰 . 初中数学跨学科项目式学习的教学实践与思考：以“土圭遇数，九畿见学”为例 ［J］. 中学数学月刊，2024

（3）：46 - 50.

［3］黄贤明，徐敬元 . 跨学科融合的数学教学：苏科版初中数学教材的案例分析与思考［J］.中学数学月刊，2024（2）：52 - 55 + 70.