基于深度学习的高中数学STEM项目设计
作者: 罗震
[摘 要] 基于深度学习理论设计的高中数学STEM项目,融合了三角函数的概念、测量珠峰的历史背景以及测量建筑物高度的日常生活场景. 在项目式教学中,通过引导学生亲手制作测量仪和开展科学实验来掌握三角测量法,不仅可以增强学生分析和解决问题的能力,促进他们对数学概念的深入理解和实际应用,还能有效提升学生的核心素养水平.
[关键词] 深度学习;STEM项目;测量
深度学习与传统的浅层学习和机械学习不同,它强调素养的培养,要求学习者整合已有的知识信息,重视批判性理解,主动构建知识体系,并将知识迁移到新的情境中解决问题,实现深度理解,促进高阶思维与能力的发展. 生活化的STEM项目基于真实情境的问题解决,以学生为主体,具备跨学科、趣味性、体验性、情境性、协作性和实证性等核心特征. 这种学习方式能够促进学生的深度学习,并对其未来工作和生活产生深远的影响,与新课标提出的核心素养目标高度一致. 接下来,本文以测量建筑物高度为例,探讨如何在高中数学教学中融入深度学习的STEM项目.
设计思路
本设计以人教A版高中数学教材(2019版)必修第一册第五章三角函数的教学内容为基础. 本章节的核心概念是“三角函数”,结合此概念,探讨测量建筑物高度的原因如下:①时代背景. 我国在2020年对地球第三极——珠穆朗玛峰的高度进行了重新测量,得出其高度为8848.86米. 从科学的角度来看,由于地球板块运动和地震等自然因素的影响,我国青藏高原地区的环境持续发生着变化. 对珠峰进行重新测量,可以直观地反映出这些变化的过程. 此外,2015年4月尼泊尔发生的8.1级大地震是否对珠峰的高度产生了影响,以及影响的程度如何,在全球范围内一直存在争议. 只有通过精确的测量,我们才能得到确切的答案. ②生活场景. 测量高度是实际应用中常见的问题,学生在初中阶段已经学习了直角三角形相关知识.
S(科学):珠峰在地理上的意义;珠峰测量的历史;海拔高度.
T(技术):直接测量与间接测量;三角形测量法的基本原理;认识测量珠峰的技术和方法.
E(工程):制作测量仪;用不同方法测量学校内外建筑物的高度;评估不同方法的优势和局限性.
M(数学):三角形的性质;比例与相似;三角函数;三角测量的数学史.
教学过程
1. 创设情境,提出任务
作为地球之巅,人类对珠穆朗玛峰的认识最初源于对其高度的测量. 1852年,英国人利用大地三角测量法,在印度平原上测得珠峰的高度为8840米. 到了20世纪初,印度当局又从大吉岭附近进行测算,得出珠峰的高度为8882米. 在过去的三个世纪里,多个国家都曾获得过珠峰的高度数据. 然而,由于测量是一项复杂的系统工程,珠穆朗玛峰究竟有多高,始终没有一个确定的答案. 因此,人们从未停止过尝试,利用新技术来寻找更精确的珠峰高度. 2020年,科学家们是如何测量珠峰的高度的呢?(通过视频引导学生了解)
常见的测量方法:对一个物体的物理特性进行测量的方法主要有两种——直接测量和间接测量.
直接测量法:无需借助数学模型的计算,使用测量精确度较高的仪器直接获得测量结果的方法. 例如,书本尺寸和人身高的测量.
间接测量法:将一个待测量分解为若干可以直接测量的量,而后利用定义或规律导出的关系式(即测量式)进行计算或作图,从而间接获得测量结果的方法. 例如,山的高度、地球的半径、地球与太阳的距离等,适合采用间接测量法. 在间接测量法中,有一种常用到的方法叫三角测量法. 它将被测物体构建成一个或多个三角形,通过测量三角形边长、角度等数据,间接计算出被测物体的高度(或距离). 今天,我们将采用这个方法来测量建筑物的高度. 需要完成以下任务:
任务1:以小组为单位制作一款简易的测量仪,并说明它的原理.
任务2:使用自制的测量仪测量一座学校外的建筑物的高度(该建筑物能从学校操场上看见但无法接近).
2. 问题导向,激发思维火花
(1)问题分析
在活动开始前,教师引导学生积极思考:要测量学校内建筑物的高度(例如教学楼或旗杆),我们需要知道些什么?哪些工具可以协助我们进行测量?为什么选择这些工具?你的测量方案是什么?
(2)提出方案
小组成员展开头脑风暴,分享各自的设计方案. 预设方案和测量方法如下:
①直角三角形法:通过测量仰角来计算高度. 追问:如何测量这个仰角?
②日影法(泰勒斯法):通过测量太阳的影子长度来计算高度. 采用日影法进行测量,仅需一把皮尺即可完成任务. 在实际应用此方法时,需分别测量某一时刻的人的身高和影子长度,以及建筑物的影子长度,这样就可以利用相似三角形的原理计算出建筑物的高度.
③比例法:通过参照物的高度按比例计算目标的高度. 追问:参照物应如何选择和放置?人们是如何运用参照物进行测量的?是否存在特定的位置要求?
④物理法:通过测定自由落体的时间来计算建筑物的高度. 追问:如何测定自由落体的时间?
追问:这四种方法的优势和限制条件是什么?
3. 合作探究,实践体验
实际上,上述四种测量方法都存在一定的现实限制. 例如,日影法在阴天条件下无法执行,而直角三角形法和比例法在遇到障碍物时同样难以实施. 鉴于这些局限性,我们可以采用一种更为通用的测量方法.
任务1 工程制造——制作测量仪.
(1)任务分析:在活动开始前,教师鼓励学生主动思考,说一说想设计哪种用途的测量仪,描述其特点,并列出制作它需要准备的材料.
(2)提出设计方案:小组成员开展头脑风暴,分享各自的设计方案,并在聆听团队成员的发言时,记录下对不同方案的见解.
(3)选择方案:①综合多方观点选择一个最佳方案,简要解释选择的原因. ②画出设计草图,并注明所用材料和用途.
(4)实施方案:①制作过程分为几步?根据方案,通过绘图或文字阐明制作过程. ②小组成员如何分工?按照分工任务动手制作测量仪.
测量仪的制作方案参考:首先,将量角器复印并放大5倍. 接着,在放大后的量角器中心点固定一条绳子,并在绳子的另一端悬挂一个铅锤. 这样可以轻松测量出视线与绳子之间的夹角,进而计算出所需的仰角.
设计说明 一方面,任务应根植于真实的生活情境;另一方面,它需要融入三角函数知识. 解决真实任务不仅需要学生之间的合作交流,还需要教师的参与. 大家共同收集和分析资料,提出假设并进行验证,最终评价学习成果.
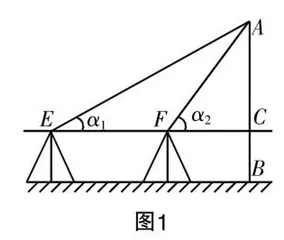
任务2 利用自制的测量仪测量一座学校外的建筑物的高度(该建筑物能从学校操场上看见但无法接近),如图1所示.
(1)测量方法:将自制的测量仪安装在三脚架上,并将其放置在适当的位置F,调整测量仪的角度,使其对准被测建筑物的顶端,计算并记录下仰角α2,接着移动到位置E,重复上述步骤,计算并记录下另一个仰角α1. 利用三角函数的相关知识,计算出该建筑物的高度AB=EF·tanα2·tanα1/tanα2-tanα1+BC.
(2)测试方案:依据评价标准,对小组制作的测量仪进行评分.
(3)改进方案:
①根据测试成果对制作的测量仪进行改进——指出哪些部位需要改进,为什么要进行改进.
②请小组阐明改进测量仪的具体步骤,并画出改进后的测量仪模型草图.
③按照修改方案,改进或重新制作测量仪.
④测量结果是否存在误差?误差产生的原因是什么?又该如何改进?
4. 展示交流、评价并反思
各组派代表展示并陈述测量仪的制作过程和测量结果. 两项任务按照表1所示的评价标准进行评估.
设计说明 完成一个作品有助于深化对三角测量法的理解和应用,通过成果交流分享,可以促进相互学习并引发反思. 反思阶段的主要目的是让学生和教师对学习过程进行深入的总结. 整个过程展示了实践体验、内化吸收、探索创新,从而帮助学生获得更为全面和具体的知识,推动深度学习的进程.
5. 迁移应用,加深概念理解
通过构建与目标物体相关的三角形,将难以直接测量的物体高度转换为易于测量的长度等数据,这便是三角测量法的基本原理. 在测量诸如珠穆朗玛峰这样庞大的物体时,必须考虑更多因素,例如地球曲率、重力场的影响以及海拔高度等. 在实际测量过程中,科学家会在珠峰顶端设置一个反射器(觇标),而地面上的测量人员则使用仪器对准这个反射器. 这种仪器能够发射并接收红外激光信号,当激光击中反射器时,会被反射回来. 通过测量激光往返的时间,便能计算出仪器与反射器之间的直线距离. 随后,科学家利用三角函数计算出珠峰的确切高度. 为了减少误差,科学家在珠峰底部设立了七个观测点,同时进行高度测量,这充分体现了科学家对科学严谨性的不懈追求.
教学反思
1. 需要更新教学观念,树立STEM教育理念
基于深度学习的STEM项目打破了传统教学孤立传授学科知识的做法,转而注重对课本知识的深入加工和处理,以及基于真实情境的问题解决,强调知识的综合运用,着力培养学生的创新意识. 随着社会的发展,未来的社会需要大量的复合型人才,因此教育体系需要作出相应的调整,以适应未来社会生产力发展的需求. 在新时代素养导向的教学背景下,数学教师面临着更大的挑战. 高中数学教师应当加强自我学习,紧跟未来教育的发展趋势. 本项目设计拓展探究了数学知识在实际问题中的应用:以测量珠穆朗玛峰的高度作为背景引入课题,通过测量学校内外建筑物的高度来驱动项目,以测量方法作为问题导向,以制作简易测量仪作为工程实践,将项目式学习与探究式学习相结合,有助于学生深入理解数学知识.
2. 变革教学方式,促进核心素养达成
将深度学习理论应用于高中数学STEM项目设计,是实现数学学科育人目标的重要途径,它有助于培养学生的跨学科思维能力,并使数学知识与学生的生活更加贴近. 跨学科教育强调的不再是单一学科的深入学习,也不再局限于学科间的界限,而是通过整合多学科知识,提升学生解决实际问题的能力. 近年来,新高考数学命题的趋势显示,将人文史料与STEM(科学、技术、工程和数学)元素相结合,强调数学的实际应用已成为命题特色. 因此,数学教师应当深入研究新的课程标准和教材,探索数学与其他学科知识的交汇与融合之处,加强与其他学科教师的合作与交流,利用新技术手段,创造多样化的学科情境,以此在数学教学活动中拓展学生的思维空间,进而提高学生的核心素养,强化教育的育人效果.