基于深度学习的“问题导向式教学”的实践探索

［摘  要］ 针对高三数学复习课效率低下的问题，研究者以一节高三专题复习课为例，阐述如何在课堂教学中提高教学效果，并对通过问题导向的教学法促进学生深度学习进行了实践探索，发现“问题导向式教学”能够促进学生在数学学习过程中渗透情感，帮助学生深刻理解核心概念，提高思维深度，并深度整合知识，实现深度学习.

［关键词］ 深度学习；问题导向式教学；核心素养

问题缘起

《普通高中数学课程标准（2017年版2020年修订）》（下文简称新课标）提出：通过高中数学课程的学习，学生能获得基础知识、基本技能、基本思想、基本活动经验，提高从数学角度发现问题、提出问题、分析问题和解决问题的能力，发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养［1］. 专题复习是高中数学课程学习的一种重要方式.

目前，高三数学复习课主要存在以下三种情况.

（1）引入太形式，学生思维无处落脚.

通过罗列知识点来引入课程：利用PPT展示关键知识点，并引导学生逐条回顾；在知识点上刻意留白，鼓励学生自行填空. 这种引入方式，用时不少，但学生对知识点没有印象，即使有印象也仅仅流于表面，思维不够深入. 未设置引入环节，直接开始讲题，等学生反应过来，一道例题已经讲解过半，学生的思维与课堂严重脱节.

（2）例题不典型，学生思维无法生长.

例题繁多且杂乱无章，缺乏逻辑联系，或者同一类型的例题反复出现. 这样的课程设计导致学生无法掌握“四基”，无法提升“四能”，数学素养也难以有效提高.

（3）课堂无升华，学生思维无处聚焦.

就题论题，只把题讲完，没有提炼通性通法；课堂小结仅限于罗列知识点，完全是走走形式，没有深度整合知识，学生思维难以有效提升.

高三复习不仅应重视学生掌握“四基”，还应着重培养学生的深度学习能力，促进思维能力的发展，以及提升数学学科核心素养. 通过问题导向式教学，引导学生在持续发现、分析和解决问题的过程中，深化学习体验，进入深度思维模式，进而提高数学学科核心素养.

本文以“利用导数研究函数单调性”的高考专题复习课为例，探讨如何利用“问题导向式教学”促进学生进行深度学习.

概念界定

1. 深度学习

深度学习是由瑞典教育心理学家费伦茨·马顿（Ference Marton）和罗杰·赛尔乔（Roger Saljo）提出的，关注学生的学习动机、知识体系、学习观念、反思状态、学习结果、思维层次以及学习投入程度. 深度学习主要指多维度、多模式的综合学习和整体学习，旨在培养高层次的思维能力［2］. 深度学习是学生必备的能力，主要包括掌握学科核心知识、批判性思维、解决复杂问题、团队协作、有效沟通以及学会学习六个维度的基本能力. 总而言之，深度学习是一种提升高阶思维能力的学习方式，是一种学生积极参与、高度投入的学习过程，是一种学生的认知、情感、技能都会进入更高境界的学习结果［3］.

2. 问题导向式教学

问题导向式教学指根据教学目标及重难点来设计问题，通过问题来主导教师的“教”及学生的“学”［4］. 问题贯穿整个课堂流程，从情境引入、例题讲解、变式拓展到总结巩固，各个环节都充满问题. 问题形式多样，可以是问题链，也可以是例习题；可以是书面的，也可以是口头的. 问题解决方式多元，可以让学生独立思考，也可以让学生合作探究甚至课后翻阅资料等. 问题设置既能培养学生思维的逻辑性和广阔性，又能培养学生思维的深刻性和全面性，更能培养学生思维的创新性.

问题导向式教学能够促进学生深度学习. 深度学习要求教师设计富有目标性、能够激发学生积极参与的学习活动. 问题导向式教学通过逐步深入的问题链，为学生设定明确的学习目标，激发他们主动探索和学习的热情；引导学生围绕核心问题进行深入思考，以实现深度学习的目标；促使学生不断向更高层次的思维迈进，从而持续提升思维能力. 学生通过分析不同层次的问题，培养思维的发散性；通过探究核心问题，培养思维的深刻性. 总之，创设具有导向作用的问题链能激发学生的思维，培养学生问题解决能力和高阶思维能力.

实践策略

1. 深度学习的落脚点——引入精彩问题，促学生情感深度渗透

学生在学习中的情感包括学习的信心、兴趣、积极性以及主动性等. 复习课是学生对已知内容的再学习、再整合的过程. 由于内容是之前已经学习过的，部分学生认为自己都懂，以至于不够投入. 因此，在复习课中引入恰当的问题至关重要，它能够迅速激发学生的思维，使他们投入到课堂中，并为他们深入学习提供坚实的基础. 笔者认为，应遵循以下几项原则：

（1）引入学生熟悉的问题情境，激发他们的学习兴趣.

（2）引入直观且易懂的问题情境，确保高中数学课程面向全体学生，实现“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”. 教师应针对不同层次学生的实际情况，深入挖掘例习题的多种功能，制定适合各个学生发展的教学方案，以激发不同层次学生的学习信心.

（3）引入具有挑战性的问题情境. 高考题目是高三学生急于挑战的问题，特别是那些之前认为复习内容缺乏新意的学生，面对高考题目时都跃跃欲试，从而激发学习积极性.

（4）引入具有导向性的问题情境. 通过改编课本中的问题，或寻找高考题目在课本中的“题根”，引导学生重视课本，激发他们回归课本的主动性.

【教学片段1】

通过PPT提出以下两个问题：

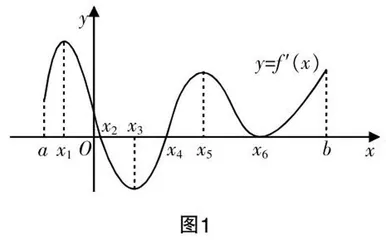
（1）函数f（x）的导函数y=f′（x）的图象如图1所示，则函数f（x）的增区间是________.（人教A版选择性必修第二册第92页练习第1题改编）

（2）已知函数f（x）=aex－lnx在区间（1，2）上单调递增，则a的最小值为（  ）（2023年高考全国Ⅱ卷第6题）

A. e²  B. e  C. e^-1  D. e^-2

师：在区间（a，b）上，若f′（x）>0，则f（x）在（a，b）上单调吗？如果单调，是单调递增，还是单调递减？

生1：单调递增.

师：若f（x）在（a，b）上单调递增，则在区间（a，b）上f′（x）>0恒成立吗？为什么？

生2：不一定，例如第（1）题，函数f（x）在区间（x₄，b）上单调递增，但f′（x₆）=0.

师：函数单调性发生改变的“点”与导函数有什么关系？

生3：是导函数的变号零点.

师：请总结函数的单调性与导函数的符号之间的关系.

生4：f（x）在（a，b）上单调递增，是f′（x）>0在区间（a，b）上恒成立的必要不充分条件；f（x）在（a，b）上单调递增的充要条件是f′（x）≥0在区间（a，b）上恒成立且f′（x）=0的点不构成一个区间.

第（1）题是一道难度适中的教材练习改编题，旨在有效激发学生的学习信心，并引导他们主动回归教材. 第（2）题是一道高考真题，旨在充分调动学生学习的积极性，让学生尽快融入课堂学习之中. 深度学习的首要步骤是学习情感的深度渗透. 将情感融入课堂，为思维的主动参与和深入学习奠定基础，是深度学习的落脚点.

2. 深度学习的孕育点——展示典型例题，促核心概念深度理解

典型例题首先应该聚焦于数学的核心概念和通性通法，以促进学生思维能力与创新意识的发展. 通过解答教师设置的典型例题，学生不仅能够提炼出解决一类问题的数学方法，还能够学会用规范的数学语言表述问题，同时深入理解数学内容的本质，领会其中所蕴含的数学思想，提升思维水平，进而推动深度学习.

【教学片段2】

例1 （1）求函数f（x）=sinx－x的单调区间. （人教A版选择性必修第二册第86页例1（2）改编）

（2）判断函数f（x）=lnx－x+1/x-1的零点的个数. （2019年高考新课标Ⅱ卷理科第20（2）题）

师生一起完成例1.

问题：利用导数求函数的单调区间包括几个步骤？

生5：包括三个步骤——求f′（x）；求f′（x）的零点；确定f（x）的单调区间.

追问1：你认为例1的第（2）题部分同学出现错误的原因是什么？

生6：忽略了定义域，因此生5的回答中应当补充一个步骤——求定义域.

生7：我认为f′（x）的零点不一定是f（x）的单调区间的端点.

追问2：你还有其他补充吗？

生8：判断f′（x）的零点是否为变号零点.

以问题为导向，学生之间相互补充，教师协助完善，从而得出求函数单调区间的步骤如下：①求定义域；②求f′（x）；③确定f′（x）的变号零点；④讨论f′（x）的变号零点是否在定义域内；⑤变号零点将定义域划分为若干个区间，确定f′（x）在每个区间的符号，写出单调区间.

第（1）问求的是具体函数的单调区间，虽然其导函数有无数个零点，但函数仍然是单调的，旨在激发学生对函数单调性与导数之间关系的深入思考. 第（2）问应用函数的单调性判断零点的个数，学生容易忽略函数的定义域，错误认为函数f（x）=lnx－x+1/x-1的单调递增区间是（0，+∞），从而得出函数f（x）=lnx－x+1/x-1只有一个零点的不正确结论. 本问题旨在激发学生对求解函数单调区间基本步骤的思考；通过研究具体函数的单调区间，帮助学生顺利过渡到对含参函数单调区间的深入思考. 通过应用导数来求解函数的单调区间，学生能够培养积极探索问题的习惯，深入理解核心概念，从而促进深度学习，并发展思维能力.

3. 深度学习的生长点——探究变式问题，助思维深度提升

变式是指在原有例题的基础上，通过改变例题的条件、改变例题的结论、交换例题条件与结论的位置、改变例题的设问方式、把例题的难点和知识点提升至更高层次以及将问题的结论一般化并进行推广等［5］. 学生通过独立思考和合作探究的方法来应对变式问题，可以提高团队协作和解决复杂问题的能力，推动深度学习，并培养思维深度.

【教学片段3】

例2 已知f′（x）=x-a/x²，其中a>0，x>0，则f（x）的增区间是_____.

师生共同完成例2后，教师布置以下任务：

（1）自主探究，独立思考，完成变式题1至变式题4.

变式题1：已知f′（x）=（a+1）x-a，其中a>0，x>0，则f（x）的增区间是___.

变式题2：已知f′（x）=-x²+（a+1）x-a/x²，其中a>0，x>0，则f（x）的增区间是___.

变式题3：试讨论函数f（x）=1/x－x+alnx的单调区间.

变式题4：试讨论函数f（x）=1/x－ax+lnx的单调区间.

（2）合作探究，小组讨论，完成问题1至问题5.

问题1：利用导数求函数的单调性的本质是什么？

问题2：例2与变式题1、变式题3、变式题4的联系和区别分别是什么？

问题3：变式题1与变式题2在解答过程中存在哪些差异？导致这些差异的原因是什么？