以“基本思想”为主题的数学单元教学案例

［摘  要］ 文章以概率的求解为例，探讨以“基本思想”为主题的数学单元教学案例设计，呈现从概率问题的剖析到方法思维框架的构建、从概率知识的归纳到数学思想方法的提炼、从例题练习的解决到概率问题的一般求解策略的总结等渗透数学基本思想的教学过程设计，并从凸显联系的观点、注重过程性知识、形成文本化经验等三个方面浅谈设计反思.

［关键词］ 概率；分类；分步；模型；教学设计

过程性知识的习得是单元教学的重要价值，在前两个课时的教学中，两类模型（二项分布模型和超几何分布模型）的生成过程离不开概率问题的求解方法，为了进一步深化学生对概率求解方法这一过程性知识的理解，促进学生感悟推理思想，团队设计并实施了第3课时“概率的求解”. 下文分享教学过程设计，以待指正.

基本情况

1. 内容分析

概率的求解是概率知识的综合应用，与直接应用概率公式或模型求解不同，本节课定位于概率知识综合应用的基本活动经验的形成与应用.本节课设置在二项分布与超几何分布知识学习之后，其上位知识包括样本空间、事件的关系与运算、概率的基本性质与运算、概率模型等，这些知识及其学习过程蕴含着丰富的数学思想方法. 概率性质中互斥事件、对立事件蕴含着分类思想，概率公式中相互独立事件的概率乘法公式、条件概率乘法公式蕴含着分步思想，全概率公式蕴含着分类与分步思想，古典概型、二项分布、超几何分布蕴含着模型思想，等等. 概率求解过程是“目标事件分析（直观分析方法、分类思想与分步思想、模型思想的应用）—目标事件表示（和事件、积事件的表示）—目标事件概率计算（加法公式、乘法公式、概率模型的应用）”的研究过程，体现着推理思想与模型思想.

2. 学情分析

样本空间、事件的关系与运算、概率的基本性质与运算、概率模型等是概率求解的知识基础. 从一般的“概率的求解”的整体视角学习特殊的“分布列模型（二项分布、超几何分布）”的局部视角的数学活动经验，渗透着应用概率加法公式与乘法公式，以及概率模型求解概率的基本技能，这些都是综合应用概率知识求解概率的思维基础. 概率综合问题的情境较之前的问题更加复杂，需要学生具有较好的分析问题的能力；学生在之前应用概率知识求解概率问题时，多处于公式或模型的套用，重题目机械式训练，忽略了题目之间的联系，缺乏对解题活动经验的深层次挖掘，教学需要引导学生归纳概率知识与问题蕴含的思想方法，形成概率求解一般策略.

3. 教学目标

（1）复习回顾二项分布、超几何分布的研究过程，归纳概率问题的基本求解方法，初步形成应用概率公式或模型求解概率的思维框架，感悟推理思想.

（2）梳理求解概率的公式或模型，剖析其蕴含的数学思想方法，从分类思想、分步思想、模型思想的角度理解概率知识，感悟推理思想、模型思想.

（3）通过例题教学，概括形成概率问题的一般求解策略，能从思想方法的角度分析与解决概率问题，感悟推理思想.

（4）通过练习，掌握概率问题的一般求解策略，感悟推理思想.

4. 重点和难点

重点：概率知识蕴含的数学思想方法，求解概率问题的一般策略.

难点：求解概率问题的一般策略的形成.

教学过程设计

1. 复习回顾

问题1 请结合问题“已知100件产品中有8件次品，分别采用有放回和不放回的方式随机抽取4件，设抽取的4件产品中次品数为X，求随机变量X的分布列”回顾二项分布与超几何分布学习过程中求解概率的基本方法.

设计意图 引导学生复习回顾有放回和不放回随机抽样概率问题的求解过程，梳理两类求解概率的基本方法：①应用概率加法公式和乘法公式求解；②应用概率模型（古典概型、二项分布模型、超几何分布模型）求解，初步形成求解概率问题的思维框架.

2. 总结提炼

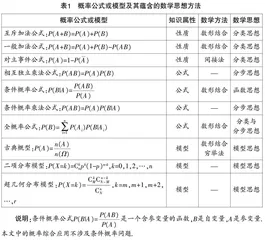
活动 请根据表格梳理常见的求解概率的公式、模型，思考这些概率知识蕴含了哪些数学思想方法？

学生活动：4人一组共同梳理相关知识，讨论挖掘知识蕴含的数学思想方法.

教师活动：①引导学生从概率性质、公式、模型等角度梳理知识；②引导学生联系样本空间、计数原理等知识，挖掘思想方法.

活动预设结果如表1所示.

设计意图 组织学生梳理概率公式或模型，挖掘知识蕴含的数学思想方法，从性质、公式、模型等角度对知识进行分类，从概率公式或模型的学习过程中归纳数形结合、穷举法等样本空间的分析或表示方法，从分类思想、分步思想、模型思想等维度构建数学思想与知识属性之间的关系，为综合应用概率知识，形成概率问题的一般求解策略做好铺垫.

3. 例题精讲

例题 设袋中有6个白球、4个黑球，从中依次取球，当取出3个相同颜色的球时停止取球，记X为取出的球的总数.

（1）若每次取球时记录颜色后放回，求X=4的概率；

（2）若每次取球时记录颜色后不放回，求X=4的概率.

师生活动：由教师带领学生共同完成第（1）问，再由学生自主完成第（2）问，教师点评.

教师活动：展示第（1）问的解题过程（如表2所示）.

设计意图 通过设计具有挑战性的概率问题，全面覆盖求解概率问题需要用到的概率知识与数学思想方法，引导学生按照“目标事件分析—目标事件表示—目标事件概率计算”的研究过程分析并解决问题. 通过设置两个相似问题，组织学生在教师示范求解第（1）问的基础上，模仿完成第（2）问的求解，引导学生经历求解概率综合问题的全过程，帮助学生积累数学活动经验，促使学生感悟推理思想.

问题2 请根据例题的求解过程，总结归纳概率问题的一般求解策略.

设计意图 引导学生找出求解过程中体现数学思维的关键环节，即“目标事件分析”，总结归纳较为完善的概率问题的一般求解策略：①结合分类思想分析目标试验包含的试验结果（样本点）并用和事件表示；②结合分步思想分析每一类试验结果包含的试验步骤并用积事件表示；③结合模型思想分析每一步包含的随机试验对应的概率模型或概率值；④用文字、符号规范表达并计算求解. 提升学生的推理能力.

4.？摇练习巩固

如表3所示.

设计意图 设置思维水平层次逐层提高的练习题目，丰富策略应用过程的多样性，深化分类思想、分步思想、模型思想等，为课堂小结进一步完善概率问题的一般求解策略做好铺垫.

5. 课堂小结

如图1所示.

设计意图 综合例题与练习的教学，进一步完善概率问题的一般求解策略.通过课堂小结将数学活动经验文本化，引导学生把隐性知识变为显性知识，形成解题工具，实现思维可视化，完善认知结构.

6.？摇课时评价设计

如表4所示.

设计意图 题目1、题目2、题目3均以强化概率问题的一般求解策略为评价目标，其中题目3通过设置复杂的情境，促进学生提高分析问题的能力，帮助学生积累基本活动经验.

设计反思

本节课关注隐性知识，重视学习迁移的发生. 通过挖掘问题与知识蕴含的方法与思想，形成解题策略，深化推理思想.梳理本节课三个教学生成点如下：

1. 凸显联系的观点

从联系的观点挖掘“二项分布与超几何分布”单元教学内容的共性是单元教学的基础，二项分布与超几何分布在模型生成的教学环节，都从整体视角出发，以概率问题的求解为教学中心，将模型作为方法提炼的产物，“概率的求解”正是两类模型学习共性的体现. 此外，本节课还从联系的观点挖掘概率公式、模型蕴含的数学思想方法的共性，引导学生学会用数学眼光深层次理解数学知识.

2. 注重过程性知识

基础知识与基本技能的学习是显性知识的学习，基本思想与基本活动经验是在“双基”学习的基础上，更易于迁移的过程性知识. 本节课注重引导学生经历从概率问题的剖析到方法思维框架的构建、从概率知识的归纳到数学思想方法的提炼、从例题练习的解决到概率问题的一般求解策略的总结等全过程，跳出“一题一法”的教学局限，引导学生从“一题一法”到“多题一策略”，积累基本活动经验，培养整体观念下的系统思维.

3. 形成文本化经验

基本思想的感悟依托于基本活动经验的积累与应用. 把知识与技能比作“道路”，基本活动经验就是“地图”，知识与技能的学习是“道路记忆”，积累活动经验是“地图记忆”. 要更好地帮助学生积累数学活动经验，需要尽可能将数学活动经验文本化，形成可视化的“思维地图”，引导学生在应用“思维地图”的过程中不断细化、完善“思维地图”，感悟数学思想.

基金项目：广东省基础教育学科教研基地项目，广东省于涛名教师工作室，广东省教育研究院中小学数学专项课题“基于大观念的高中数学单元教学实践研究”（GDJY-2022-M-b124）；广东省教育科学规划课题“基于SOLO分类理论的高中数学学业质量评价的实践研究”（2021YQJK103）.

作者简介：于涛（1982—），本科学历，中学高级教师，广东省名教师工作室主持人，从事数学教育教学研究工作.